信号与系统笔记

信号与系统

傅里叶级数

三角形式的傅里叶级数

首先我们知道，周期函数 \(f(t)\) 可用傅里叶级数表示，形式如下 \[ f(t)=a_0+\sum^\infty_{n=1}[a_n\cos{(n\omega t)}+b_n\sin{(n\omega t)}] \] 直流分量 \(a_0\) \[ \newcommand{\diff}{\mathrm{d}} a_0=\frac{1}{T}\int^{t_0+T}_{t_0}f(t)\diff{t} \] 余弦分量的幅值 \[ a_n=\frac{2}{T}\int^{t_0+T}_{t_0}f(t)\cos{(n\omega t)}\diff{t} \] 正弦分量的幅值 \[ b_n=\frac{2}{T}\int^{t_0+T}_{t_0}f(t)\sin{(n\omega t)}\diff{t} \] 其中 \(T\) 为周期函数 \(f(t)\) 的周期。

如果用和差化积公式将两项三角函数合并为一项，则可表示为 \[ f(t)=c_0+\sum^\infty_{n=1}c_n\cos{(n\omega t+\varphi_n)} \] 或 \[ f(t)=d_0+\sum^\infty_{n=1}d_n\sin{(n\omega t+\theta_n)} \] 其中满足 \[ a_0=c_0=d_0\\ c_n=d_n=\sqrt{a_n^2+b_n^2}\\ a_n=c_n\cos{\varphi_n}=d_n\sin{\theta_n}\\ b_n=-c_n\sin{\varphi_n}=d_n\cos{\theta_n}\\ \tan{\theta_n}=\frac{a_n}{b_n}\\ \tan{\varphi_n}=-\frac{b_n}{a_n} \] 正弦、余弦分量的频率必定是基频 \(f_1=1/T\) 的整数倍，通常把频率为 \(f_1\) 的分量称为基波，频率为 \(2f_1,3f_1,\cdots\) 的称为二次谐波、三次谐波等。

从上式可以发现，\(a_n,b_n,c_n\) 是关于 \(n\omega\) 的函数，记 \(a_n=a_n(n\omega)\)，对于不同的 \(n\omega\) 值有不同的取值，绘制 \(c_n-n\omega\) 图可得

周期信号的频谱图示例

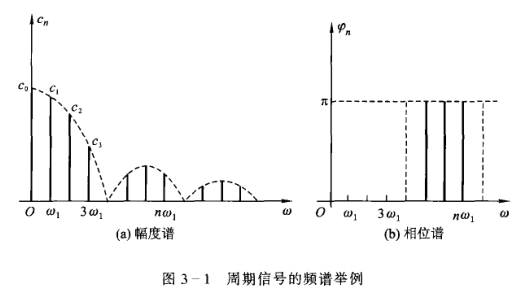
明显可以看出各频率分量的相对大小，我们把这种图称为信号的幅度频谱或简称幅度谱，图中的实线称作谱线，虚线称作包络线——反映各分量的幅度变化情况。

同理还可以绘制相位频谱或简称相位谱。

指数形式的傅里叶级数

根据欧拉公式可转换为 \[ \newcommand{\j}{\mathrm{j}} f(t)=a_0+\sum^\infty_{n=1}\left(\frac{a_n-\j b_n}{2}e^{\j n\omega t}+\frac{a_n+\j b_n}{2}e^{-\j n\omega t} \right) \] 不妨令 \[ F(n\omega)=\frac{1}{2}(a_n-\j b_n) \]

从公式知晓：

\(a_n\) 是关于 \(n\) 的偶函数，故 \(a_n(-n\omega)=a_n(n\omega)\)；

\(b_n\) 是关于 \(n\) 的奇函数，故 \(b_n(-n\omega)=-b_n(n\omega)\)；

\(F(0)=a_0\)。

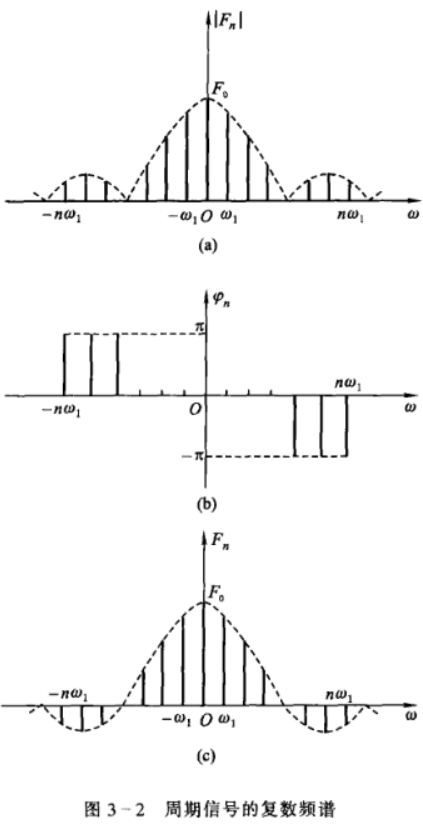
故 \[ \newcommand{\j}{\mathrm{j}} f(t)=\sum^{\infty}_{-\infty}F(n\omega)e^{\j n\omega t}\\ \] 一般也会简写 \(F_n\) \[ F_n=\frac{1}{T}\int^{t_0+T}_{t_0}f(t)e^{-\j n\omega t}\diff{t} \] 其中满足 \[ F_0=c_0=d_0=a_0\\ F_n=|F_n|e^{\j \varphi_n}\\ F_{-n}=|F_{-n}|e^{-\j \varphi_n}\\ |F_n|=|F_{-n}|=\frac{1}{2}c_n=\frac{1}{2}d_n=\frac{1}{2}\sqrt{a_n^2+b_n^2}\\ |F_n|+|F_{-n}|=c_n\\ F_n+F_{-n}=a_n\\ b_n=\j(F_n-F_{-n})\\ c_n^2=d_n^2=a_n^2+b_n^2=4F_nF_{-n} \] 同样我们可以画出指数形式下的幅度谱，又称复数频谱。其中 \(F_n\) 的大小由 \(|F_n|\) 决定，正负由相位 \(\varphi_n\) 决定，合在一张频谱图上得到

周期信号的复数频谱

周期信号的平均功率

\[ P=\overline{f^2(t)}=\sum^{\infty}_{-\infty}|F_n|^2 \]

即周期信号的平均功率等于傅里叶级数展开各谐波分量有效值的平方和，也即时域和频域能量守恒。

函数的对称性与傅里叶系数的关系

偶函数

由于偶函数满足 \[ f(t)=f(-t) \] 故傅里叶展开后只可能是偶级数，所以 \[ \begin{cases} a_n=\frac{4}{T}\int^{\frac{T}{2}}_{0}f(t)\cos{(n\omega t)}\diff{t}\\ b_n=0 \end{cases} \] 可以得到 \[ c_n=d_n=a_n=2F_n\\ F_n=F_{-n}=\frac{a_n}{2}\\ \varphi_n=0\\ \theta_n=\frac{\pi}{2} \] 且偶函数的 \(F_n\) 为实数。

奇函数

由于偶函数满足 \[ -f(t)=f(-t) \] 故傅里叶展开后只可能是奇级数，所以 \[ \begin{cases} a_0=0,a_n=0\\ b_n=\frac{4}{T}\int^{\frac{T}{2}}_{0}f(t)\sin{(n\omega t)}\diff{t} \end{cases} \] 可以得到 \[ c_n=d_n=a_n=2\j F_n\\ F_n=-F_{-n}=-\j\frac{a_n}{2}\\ \varphi_n=-\frac{\pi}{2}\\ \theta_n=0 \] 且偶函数的 \(F_n\) 为虚数。

奇谐函数

该函数满足 \[ f(t)=-f(t\pm \frac{T}{2}) \] 即每个周期发生一次翻转的函数。

可能的奇谐函数

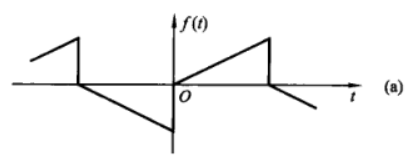
当 \(n\) 为偶数时， \[ \begin{cases} a_0=0,a_n=0\\ b_n=0 \end{cases} \] 当 \(n\) 为奇数时， \[ \begin{cases} a_n=\frac{4}{T}\int^{\frac{T}{2}}_{0}f(t)\cos{(n\omega t)}\diff{t}\\ b_n=\frac{4}{T}\int^{\frac{T}{2}}_{0}f(t)\sin{(n\omega t)}\diff{t} \end{cases} \] 可见，半波对称周期函数的傅里叶级数中，只含有基波和奇次谐波的正弦项和余弦项，故称为奇谐函数。

典型周期信号的傅里叶级数

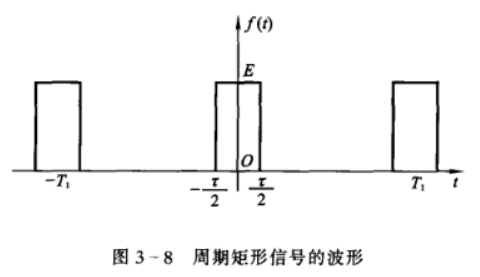
周期矩形脉冲信号

设周期矩形脉冲信号 \(f(t)\) 的脉冲宽度为 \(\tau\)，脉冲幅度为 \(E\)，重复周期为 \(T\)，有 \[ f(t)=E\left[u(t+\frac{\tau}{2}-u(t-\frac{\tau}{2}) \right] \]

傅里叶展开 $$ \[\begin{align} a_0&=\frac{E\tau}{T}\\ a_n&=\frac{2E}{n\pi}\sin{(\frac{\tau}{T} n\pi)}\\ &=\frac{2E\tau}{T}\mathop{\mathrm{Sa}}{(\frac{\tau}{T} n\pi)}\\ b_n&=0 \end{align}\] \[ 故**傅里叶级数**为 \] f(t)=+^{{}{n=1} \[ **指数形式的傅里叶展开** \] F_n= \[ 故**傅里叶级数**为 \] f(t)=^{}{-}e}{nt} $$ 可以得到频谱图

周期矩形脉冲信号的频谱图

记矩形信号的频带宽度 \(B_\omega=\frac{2\pi}{\tau}\)，或 \(B_f=\frac{1}{\tau}\)。

例如周期对称方波信号的傅里叶级数求解

周期对称方波信号

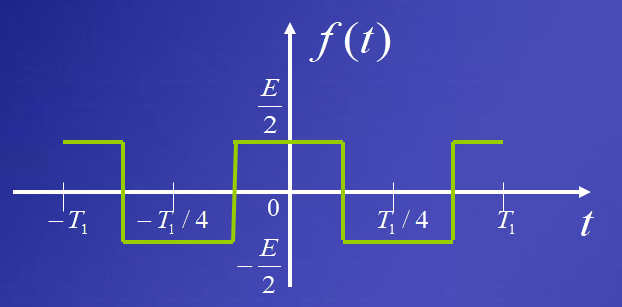
其中，幅度为 \(E\)，脉冲宽度为 \(\tau=\frac{T}{2}\)。

由于它为奇谐函数，又为偶函数，故 \[ a_0,b_n=0\\ a_n=E\mathop{\mathrm{Sa}}{(\frac{n\pi}{2})}=\pm \frac{2E}{n\pi},n=1,3,5,\cdots \]

\(\frac{2E\tau}{T}=E\)；\(\mathop{\mathrm{Sa}}{(\frac{n\pi}{2})}=\pm 1,n=1,3,5,\cdots\)；\(F_n=F_{-n}=\frac{E}{2}\mathop{\mathrm{Sa}}{(\frac{n\pi}{2})}\)。

故傅里叶级数为 \[ \begin{align} f(t)&=\frac{2E}{\pi}\sum^{\infty}_{n=1}\frac{\sin{\frac{n\pi}{2}}}{n}\cos{(n\omega t)}\\ &=\frac{E}{\pi}\sum^{\infty}_{n=1}\frac{\sin{\frac{n\pi}{2}}}{n}e^{\j n\omega t},n=1,3,5,\cdots \end{align} \]

周期锯齿脉冲信号

周期锯齿脉冲信号的波形

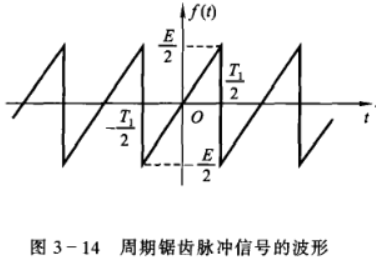
傅里叶级数为 \[ f(t)=\frac{E}{\pi}\sum^{\infty}_{n=1}(-1)^{n+1}\frac{1}{n}\sin{(n \omega t)} \]

周期三角脉冲信号

周期三角脉冲信号波形

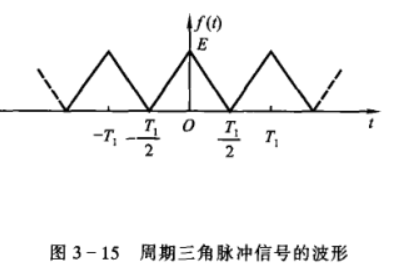
傅里叶级数为 \[ f(t)=\frac{E}{2}+\frac{4E}{\pi^2}\sum^{\infty}_{n=1}\frac{1}{n^2}\sin^2{(\frac{n\pi}{2})}\cos{(n \omega t)} \]

当 \(n\) 为奇数时，\(\sin^2{(\frac{n\pi}{2})}=1\)；

当 \(n\) 为偶数时，\(\sin^2{(\frac{n\pi}{2})}=0\)。

周期半波余弦信号

\[ f(t)=\frac{E}{\pi}-\frac{2E}{\pi}\sum^{\infty}_{n=1}\frac{1}{n^2-1}\cos{(\frac{n\pi}{2})}\cos{(n \omega t)} \]

周期全波余弦信号

即信号 \(f(t)=E|\cos{(\omega_0 t)}|\)，则 \[ f(t)=\frac{2E}{\pi}+\frac{4E}{\pi^2}\sum^{\infty}_{n=1}(-1)^{n+1}\frac{1}{4n^2-1}\cos{(2n \omega_0 t)} \]

傅里叶变换

原理

傅里叶展开是对周期信号而言的，得到的频谱图也是离散的。

拓展到对非周期函数，则是令 \(T\to \infty\)，此时拟合成周期函数，有 \(\Delta \omega=\frac{2\pi}{T}\to 0\)，频谱图从离散谱变为连续谱；同时谱线长度 \(F(n\omega)\to 0\)。

此时连续谱与我们想要的频谱图是不一样的，我们称这种连续谱为频谱密度函数。

此时 \(F(n\omega) T\) 趋近于有限值，为一个连续函数，通常记作 \(F(\omega)\) 或 \(F(\j \omega)\)，即 \[ F(\omega)=\lim_{\omega \to 0} \frac{2\pi F(n\omega)}{\omega}=\lim_{T \to \infty}F(n\omega)T \] 这样，在非周期信号下有 \[ F(\omega)=\int^\infty_{-\infty}f(t)e^{-\j \omega t}\diff{t} \] 傅里叶逆变换为 \[ f(t)=\frac{1}{2\pi}\int^{\infty}_{-\infty}F(\omega)e^{\j\omega t}\diff{\omega} \] 把这种积分形式的傅里叶级数称为傅里叶变换，即非周期信号的连续频谱表达式。

或者说把原函数从时域变换到频域（幅频坐标系）。

记傅里叶正变换 \[ F(\omega)=\mathscr{F}[f(t)]=\int^\infty_{-\infty}f(t)e^{-\j \omega t}\diff{t} \] 记傅里叶逆变换 \[ f(t)=\mathscr{F}^{-1}[F(\omega)]=\frac{1}{2\pi}\int^\infty_{-\infty}F(\omega)e^{\j \omega t}\diff{t} \] 其中 \(F(\omega)\) 是 \(f(t)\) 的频谱函数，一般是复函数，可以写作 \[ F(\omega)=|F(\omega)|e^{\j \varphi(\omega)} \] 其中 \(|F(\omega)|\) 表示信号中各频率分量的相对大小，\(\varphi(\omega)\) 表示信号中各频率分量之间的相位关系。

非周期函数的傅里叶级数也可以用 \(F(\omega)\) 表示 \[ f(t)=\frac{1}{2\pi}\int^\infty_{-\infty}|F(\omega)|\cos{[\omega t}+\varphi(\omega)]\diff{\omega} + \frac{\j}{2\pi}\int^\infty_{-\infty}|F(\omega)|\sin{[\omega t}+\varphi(\omega)]\diff{\omega} \] 当 \(f(t)\) 为实函数时，化简为 \[ f(t)=\frac{1}{\pi}\int^\infty_{0}|F(\omega)|\cos{[\omega t}+\varphi(\omega)]\diff{\omega} \]

典型非周期信号的傅里叶变换

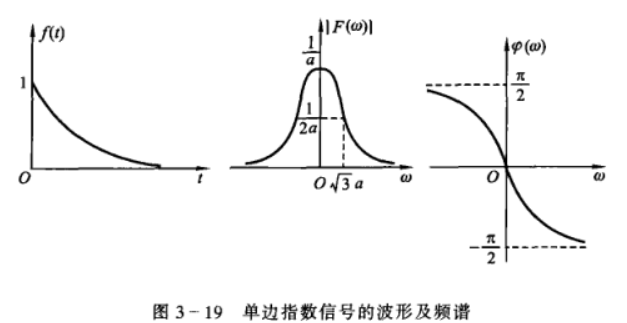
单边指数信号

即 \(f(t)=e^{-at},t\geq 0\)，其中 \(a\) 为正实数，有 \[ F(\omega)=\frac{1}{a+\j \omega}\\ |F(\omega)|=\frac{1}{\sqrt{a^2+\omega^2}}\\ \varphi(\omega)=-\arctan{(\frac{\omega}{a})} \]

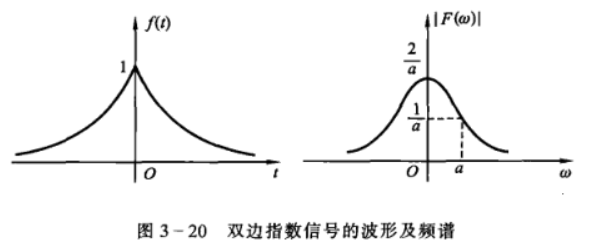
双边指数信号

即 \(f(t)=e^{-a|t|}\)，其中 \(a\) 为正实数，有 \[ F(\omega)=\frac{2a}{a^2+\omega^2}\\ |F(\omega)|=\frac{2a}{a^2+\omega^2}\\ \varphi(\omega)=0 \]

矩形脉冲信号

即 \(f(t)=E[u(t+\frac{\tau}{2})-u(t-\frac{\tau}{2})]\)，其中 \(E\) 为脉冲幅度，\(\tau\) 为脉冲宽度，有 \[ F(\omega)=E\tau\cdot \mathop{\mathrm{Sa}}{(\frac{\omega\tau}{2})}\\ |F(\omega)|=E\tau|\mathop{\mathrm{Sa}}{(\frac{\omega\tau}{2})}|\\ \varphi(\omega)=0\text{ or }\pi \]

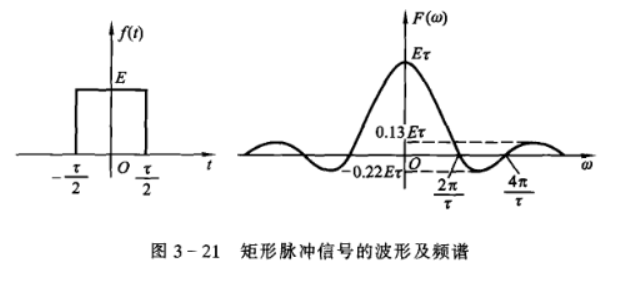
通常我们认为 \(\mathop{\mathrm{Sa}}(t)\) 函数的主要信号分布在中心频段，故其占有频率范围（频带） \[ B\approx\frac{1}{\tau} \]

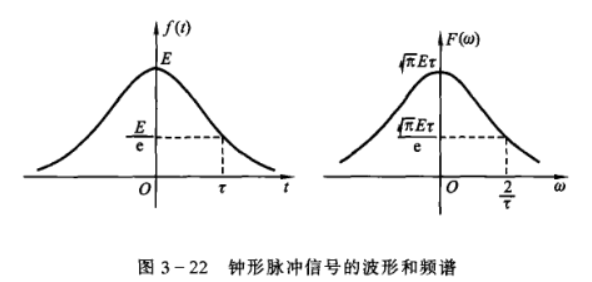
钟形脉冲信号

即高斯脉冲，有 \[ F(\omega)=\sqrt{\pi}E\tau\cdot \exp{[-(\frac{\omega \tau}{2})^2]} \] 它是一个正实函数，相位谱为零。

钟形脉冲信号的波形和频谱

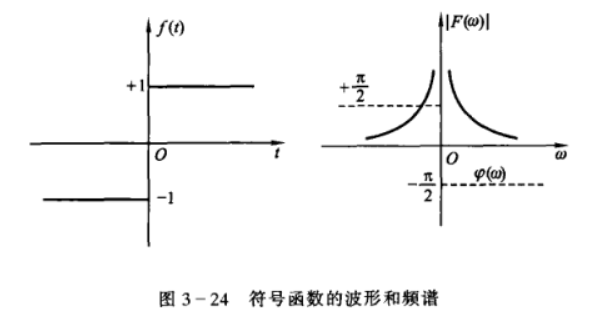
符号函数

\[ f(t)=\mathrm{sgn}(t)=\begin{cases} +1 & t>0\\ 0 & t=0\\ -1 & t<0 \end{cases} \]

有 \[ F(\omega)=\frac{2}{\j \omega}\\ |F(\omega)|=\frac{2}{|\omega|}\\ \varphi(\omega)= \begin{cases} -\frac{\pi}{2} & \omega>0\\ +\frac{\pi}{2} & \omega<0 \end{cases} \]

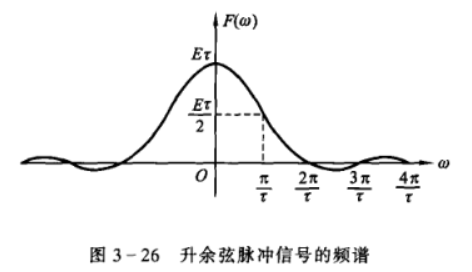
升余弦脉冲信号

\[ f(t)=\frac{E}{2}[1+\cos{(\frac{\pi t}{\tau})}],0\leq |t|\leq \tau \]

升余弦脉冲信号的波形

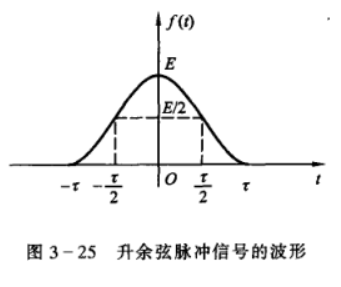
有 \[ F(\omega)=\frac{E\tau\cdot\mathop{\mathrm{Sa}}{(\omega\tau)}}{1-\left(\frac{\omega\tau}{\pi}\right)^2} \]

奇异函数的傅里叶变换

冲激函数的傅里叶变换

由冲激函数的抽样特性可知 \[ F(\omega)=\mathscr{F}[\delta(t)]=1 \]

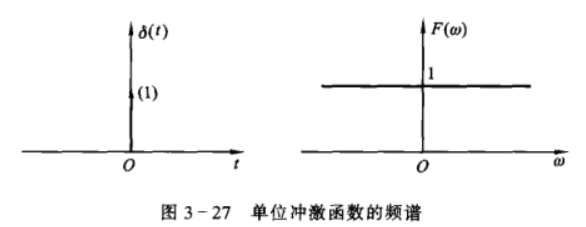
这意味着，在时域中变化异常剧烈的冲激函数包含幅度相等的所有频率分量，因此这种频谱也被称为均匀谱或白色谱。

对其冲激函数逆变换，可以找到什么样的函数的频谱为冲激函数，得 \[ f(t)=\mathscr{F}^{-1}[\delta(\omega)]=\frac{1}{2\pi} \] 结果表明，直流信号的傅里叶变换是冲激函数。

冲激偶的傅里叶变换

因为 \[ \mathscr{F}[\delta(t)]=1 \] 两边求导可得 \[ \mathscr{F}[\delta'(t)]=\j \omega \] 同理逆变换为 \[ \mathscr{F}(t^n)=2\pi(\j)^n\delta^{(n)}(\omega) \]

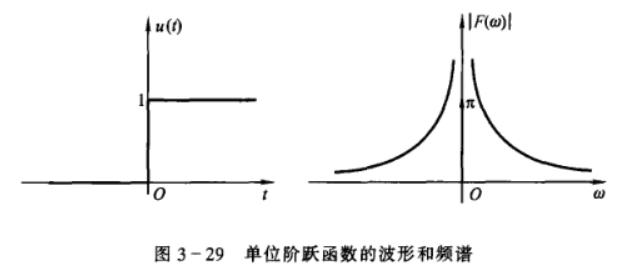
阶跃函数的傅里叶变换

因为 \[ u(t)=\frac{1}{2}+\frac{1}{2}\mathrm{sgn}(t) \] 故 \[ \mathscr{F}[u(t)]=\mathscr{F}(\frac{1}{2})+\frac{1}{2}\mathscr{F}[\mathrm{sgn}(t)] \] 即 \[ \mathscr{F}[u(t)]=\pi\delta(\omega)+\frac{1}{\j \omega} \]

傅里叶变换的基本性质

对称性

若 \[ F(\omega)=\mathscr{F}[f(t)] \] 则 \[ \mathscr{F}[F(t)]=2\pi f(-\omega) \]

若 \(f(t)\) 为偶函数则变为 \[ \mathscr{F}[F(t)]=2\pi f(\omega) \] 即 \(f(t)\) 的频谱为 \(F(\omega)\)，那么形状为 \(F(t)\) 的波形，其频谱必为 \(f(\omega)\)。

对 \(\mathop{\mathrm{Sa}}\) 函数有

时间函数与频谱函数的对称性举例

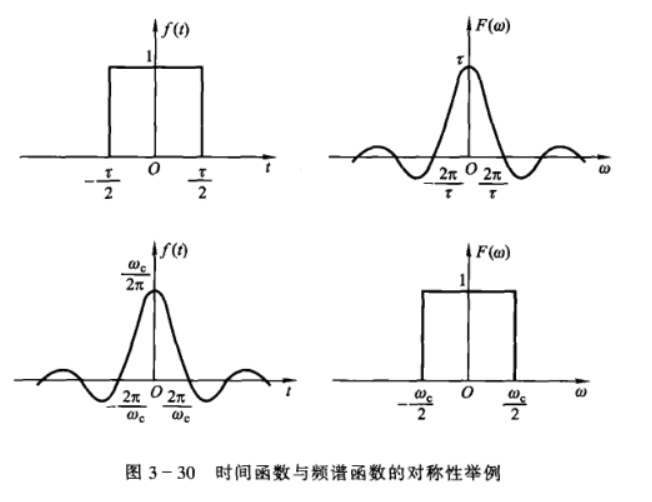
对单位阶跃信号有

时间函数与频谱函数的对称性举例

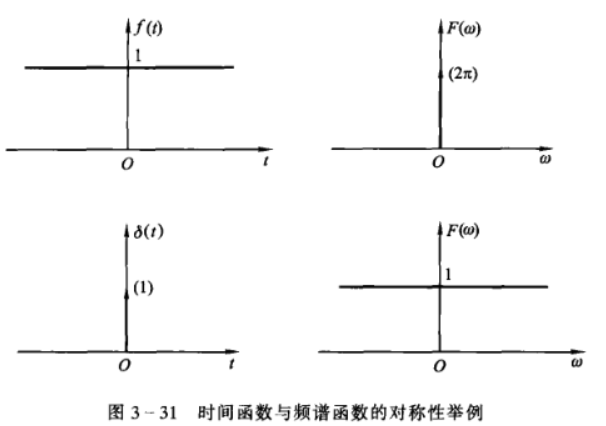
线性性（叠加性）

\[ \mathscr{F}[\sum^\infty_{i=1} a_if_i(t)]=\sum^\infty_{i=1} a_iF_i(\omega) \]

这对我们研究 LTI 系统十分有帮助。

奇偶虚实性

记 \[ F(\omega)=|F(\omega)|e^{\j \varphi(\omega)}=R(\omega)+\j X(\omega) \] 其中 \(R(\omega)\) 为实部，\(X(\omega)\) 为虚部。

当 \(f(t)\) 为实函数时，\(R(\omega)\) 为偶函数；\(X(\omega)\) 为奇函数。

可证 \(|F(\omega)|\) 是偶函数，\(\varphi(\omega)\) 是奇函数。

更进一步，

• 当 \(f(t)\) 为实偶函数，有 \[ X(\omega)=0\\ F(\omega)=R(\omega)=2\int^\infty_0f(t)\cos{(\omega t)}\diff{t} \] 即 \(F(\omega)\) 必为实偶函数。

• 当 \(f(t)\) 为实奇函数，有 \[ R(\omega)=0\\ F(\omega)=\j X(\omega)=-2\j\int^\infty_0f(t)\sin{(\omega t)}\diff{t} \] 即 \(F(\omega)\) 必为虚奇函数。

当 \(f(t)\) 为虚函数时，\(R(\omega)\) 为奇函数；\(X(\omega)\) 为偶函数。

同时满足 \[ \mathscr{F}[f(-t)]=F(-\omega) \] 对于复共轭函数 \(f^*(t)\) 同理 \[ \mathscr{F}[f^*(t)]=F^*(-\omega)\\ \mathscr{F}[f^*(-t)]=F^*(\omega) \]

尺度变换特性

\[ \mathscr{F}[f(at)]=\frac{1}{|a|}F(\frac{\omega}{a}) \]

即时域缩减 \(a\) 倍，那么频域将扩大 \(a\) 倍，幅值缩小 \(|a|\) 倍。

即信号在时域中压缩等效于在频域中扩展，反之亦然。

当 \(a=-1\) 时，\(\mathscr{F}[f(-t)]=F(-\omega)\)，这表明信号在时域中反褶等效于在频域中反褶。

通过这点可以得出，信号的等效脉冲宽度与占有的等效带宽成反比。如果要压缩信号的持续时间，就不得不以展宽频带作代价，所以在通信系统中，通信速度和占用频带宽度是矛盾的。

时移特性

\[ \mathscr{F}[f(t-t_0)]=F(\omega)e^{-\j \omega t_0} \]

信号右移（滞后）\(t_0\) 等效于在频域中乘以因子 \(e^{-\j \omega t_0}\)，即相位谱产生附加变化 \(-\omega t_0\)。

如果时移加尺度变换，则有 \[ \mathscr{F}[f(at+t_0)]=\frac{1}{|a|}F(\frac{\omega}{a})e^{\j \omega \frac{t_0}{a}} \]

频移特性

\[ \mathscr{F}[f(t)e^{\j \omega_0 t}]=F(\omega -\omega_0) \]

频谱搬移技术在通信系统中得到广泛应用，诸如调幅、同步解调、变频等。

例如 \[ \mathscr{F}[f(t)\cos{(\omega_0 t)}]=\frac{1}{2}[F(\omega+\omega_0)+F(\omega-\omega_0)]\\ \mathscr{F}[f(t)\sin{(\omega_0 t)}]=\frac{\j}{2}[F(\omega+\omega_0)-F(\omega-\omega_0)] \]

微分特性

时域微分特性 \[ \mathscr{F}\left[\frac{\diff}{\diff{t}}f(t)\right]=\j \omega F(\omega)\\ \mathscr{F}\left[\frac{\diff^n}{\diff{t^n}}f(t)\right]=(\j \omega)^n F(\omega) \] 频域微分特性 \[ \mathscr{F}^{-1}\left[\frac{\diff}{\diff{t}}F(\omega)\right]=(-\j t)f(t)\\ \mathscr{F}^{-1}\left[\frac{\diff^n}{\diff{t^n}}F(\omega)\right]=(-\j t)^n f(t) \] 应用在于，我们知道 \[ \mathscr{F}[u(t)]=\frac{1}{\j \omega}+\pi \delta(\omega) \] 那么应用微分特性可以知道 \[ \mathscr{F}[\delta(t)]=\j\omega[\frac{1}{\j \omega}+\pi \delta(\omega)]=1\\ \mathscr{F}[\delta'(t)]=\j \omega \]

积分特性

时域积分特性 \[ \mathscr{F}[\int^t_{-\infty}f(\tau)\diff{\tau}]=\frac{F(\omega)}{\j \omega}+\pi F(0)\delta(\omega) \] 频域积分特性 \[ \mathscr{F}^{-1}[\int^\omega_{-\infty}f(\Omega)\diff{\Omega}]=-\frac{f(t)}{\j t}+\pi f(0)\delta(t) \]

卷积特性（卷积定理）

卷积定理揭示了时域与频域的运算关系，在通信系统和信号处理研究领域中得到大量应用。

时域卷积定理

\[ \mathscr{F}[f_1(t)*f_2(t)]=F_1(\omega)F_2(\omega) \]

时域卷积对应频域频谱密度函数乘积。

频域卷积定理

\[ \mathscr{F}[f_1(t)\cdot f_2(t)]=\frac{1}{2\pi}F_1(\omega)*F_2(\omega) \]

频域卷积对应时域函数乘积的 \(2\pi\) 倍。

周期信号的傅里叶变换

指数信号

\[ \mathscr{F}[e^{\j \omega_0 t}]=2\pi\delta(\omega -\omega_0) \]

正弦、余弦信号

\[ \mathscr{F}[\cos{(\omega_0 t)}]=\pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]\\ \mathscr{F}[\sin{(\omega_0 t)}]=\j\pi[\delta(\omega+\omega_0)-\delta(\omega-\omega_0)] \]

余弦和正弦信号的频谱

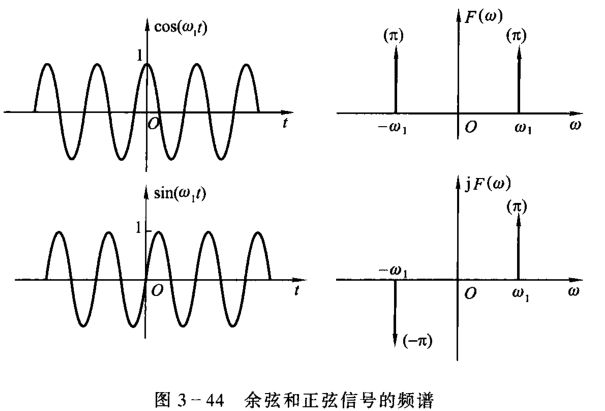
一般周期信号

设周期函数 \(f(t)\) 满足 \[ f(t)=f(t+T)\\ \omega_0=\frac{2\pi}{T} \] 指数形式的傅里叶展开为 \[ \newcommand{\j}{\mathrm{j}} f(t)=\sum^{\infty}_{-\infty}F_ne^{\j n\omega_0 t}\\ \] 傅里叶变换为 \[ \begin{align} \mathscr{F}[f(t)] &=\sum^{\infty}_{-\infty}F_n\mathscr{F}[e^{\j n\omega_0 t}]\\ &=\sum^{\infty}_{-\infty}F_n[2\pi\delta(\omega-n\omega_0)]\\ &=2\pi\sum^{\infty}_{-\infty}F_n\delta(\omega-n\omega_0) \end{align} \] 可以知道，周期信号 \(f(t)\) 的傅里叶变换是由一些冲激函数组成的，这些冲激位处于信号的谐频。

从中我们也可以知道，当 \(T\to \infty\)，即 \(\omega\to 0\) 时，频谱图中频率间隔趋近于零，此时傅里叶变换得到的频谱图将变为密度很高的冲激函数的组合，密度足够小时，即为连续图像。

同时反之也可以知道，周期信号的傅里叶变换，我们可以先选取周期信号的一个周期进行傅里叶变换，然后再间隔 \(\omega_0\) 抽样，这样也得到了周期信号的傅里叶变换。

例如周期为 \(T_1\)，脉宽为 \(\tau\) 的矩形脉冲信号，我们首先知道单周期的矩形脉冲信号的傅里叶变换为 \[ F(\omega)=E\tau\cdot \mathop{\mathrm{Sa}}{(\frac{\omega\pi}{2})} \]

我们间隔 \(\omega_0=\frac{2\pi}{T_1}\) 进行抽样冲激函数，得到结果

周期矩形脉冲信号的傅里叶变换

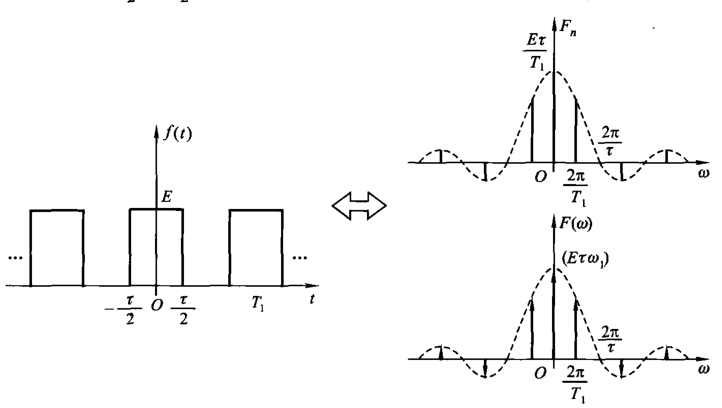
需要注意乘以 \(2\pi\)。

抽样信号的傅里叶变换

连续信号乘以抽样脉冲得到抽样信号。

抽样过程

时域抽样

我们知道，时域乘与频域卷积是等效的，那么 \[ \mathscr{F}[f(t)\cdot p(t)]=2\pi F(t)*P(t) \]

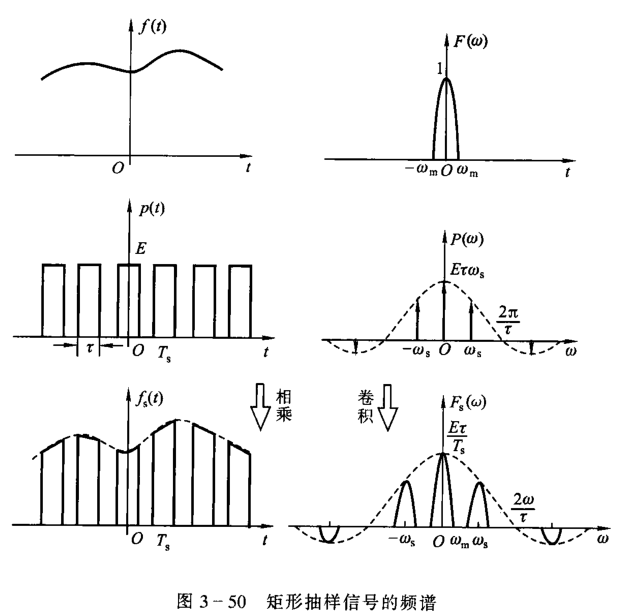
矩形脉冲抽样

矩形抽样信号的频谱

冲激脉冲抽样

冲击抽样信号的频谱

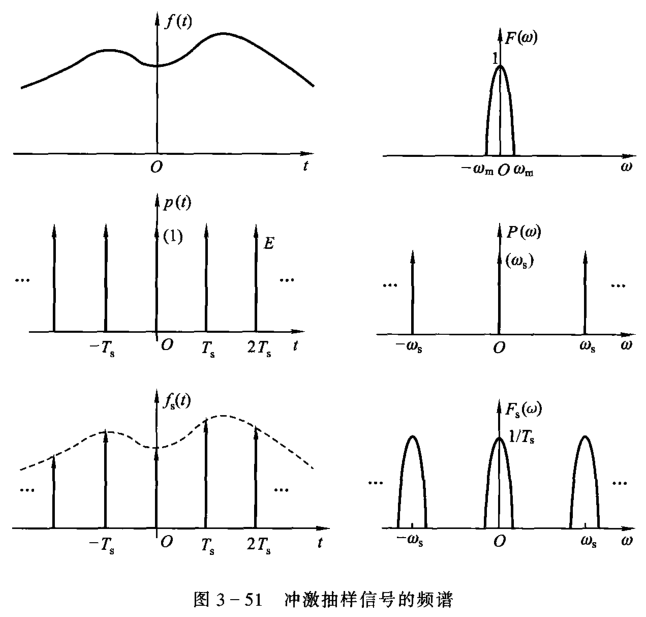
可以发现，时域抽样会使得频域信号产生周期。

频域抽样

我们在周期信号的傅里叶变换中可以知道，频域冲激抽样相当于让时域信号产生周期。

频谱抽样所对应的信号波形

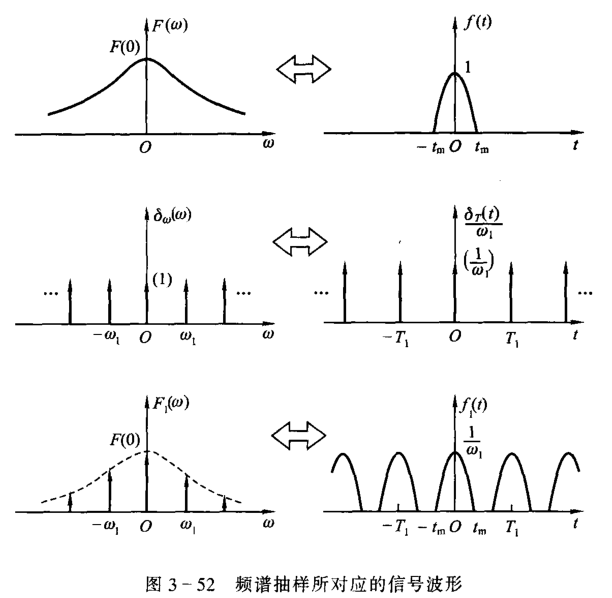
可以发现，频域抽样会使得时域信号产生周期。

特性

周期信号和抽样信号的特性

时域和频域之间，抽样其中一边的信号，会使得另一边的信号产生重复（周期）。

抽样定理

时域抽样定理

我们知道，在时域抽样会使得频域信号产生周期，也就是说实际上我们可以抽取频域信号的一个周期来还原时域信号，这就是现代数字通信的原理之一。

但是，我们会发现，如果说 \(\omega\) 越小，也就是说 \(T\) 越大，那么频域信号重复得就会越快。

我们把 \(f=\frac{1}{T}=\frac{\omega}{2\pi}\) 称作抽样频率（抽样率）。

抽样率越低，抽样的冲激信号越分散，频域信号重复得越快；

抽样率越高，抽样的冲激信号越密集，频域信号重复得越慢。

从这一点也可以得知，当抽样率趋近于零的时候，相当于周期信号的每个部分重叠在一个位置，这也是符合非周期信号的傅里叶变换的现象。

低抽样率时的抽样信号及频谱（混叠）

我们可以从图中看出，如果说频域信号产生了重叠（混叠），那么我们就无法从单一周期内的频域信号还原出完整的时域信号。

抽样定理指出：

一个频谱受限的信号 \(f(t)\)，如果频谱只占据 \(-\omega_m\sim+\omega_m\) 的范围，则信号 \(f(t)\) 可以用等间隔的抽样值惟一的表示。而抽样间隔必须不大于 \(\frac{1}{2f_m}\)，其中 \(\omega_m=2\pi f_m\)，或者说，最低抽样频率为 \(2f_m\)。

即重建原信号的必要条件为 抽样率需要大于等于最低抽样率： \[ f\geq 2f_m\text{ or }\omega\geq 2\omega_m \] 其中最大抽样间隔称为奈奎斯特抽样间隔，最低抽样频率称为奈奎斯特抽样频率。

抽样定理的物理意义为

• 对于一个频率受限的信号波形决不可能在很短的时间内产生独立的、实质的变化，它的最高变化速度受最高频率分量 \(\omega_m\) 的限制。
• 为保留波形所有频率分量的全部信息，要求一个周期的间隔内至少抽样两次。

根据抽样定理，如果想要恢复原信号，我们需要选取频域的一个周期，一般采取 \[ F(\omega)=F_s(\omega)H(\omega) \] 其中 \(F_s(\omega)\) 是抽样信号傅里叶变换后的时域信号，\(H(\omega)\) 是矩形信号 \[ H(\omega)=\begin{cases} T & |\omega|<\omega_m\\ 0 & |\omega|>\omega_m \end{cases} \] 即选取低频信号，一般是将抽样信号 \(f_s(t)\) 施加于理想低通滤波器（该滤波器的传输函数为 \(H(\omega)\)），这样就得到了频谱为 \(F(\omega)\) 的连续信号 \(f(t)\)。

频域抽样定理

由时域和频域的对称性，可以得到频域抽样定理：

若信号 \(f(t)\) 是时间受限信号，它集中在 \(-t_m\sim+t_m\) 的时间范围内，若在频域中以不大于 \(\frac{1}{2t_m}\) 的频率间隔对 \(f(t)\) 的频谱 \(F(\omega)\) 进行抽样，则抽样后的频谱 \(F_s(\omega)\) 可以惟一地表示原信号。