信号与系统笔记

发表于 2023-03-09 更新于 2023-06-15 本文字数： 8k 阅读时长 ≈ 7 分钟

有关信号与系统的简要笔记

信号与系统

系统的时域分析

经典法

一个定常系统（线性系统）对应的数学模型是一个线性常系数常微分方程。

设系统的激励信号为 \(e(t)\)，响应为 \(r(t)\)，则它的数学模型可表示为 \[ \newcommand{\diff}{\mathrm{d}} C_0\frac{\diff^n}{\diff{t^n}}r(t)+C_1\frac{\diff^{n-1}}{\diff{t^{n-1}}}r(t)+\cdots+C_{n-1}\frac{\diff}{\diff{t}}r(t)+C_nr(t)\\ =E_0\frac{\diff^m}{\diff{t^m}}e(t)+E_1\frac{\diff^{m-1}}{\diff{t^{m-1}}}e(t)+\cdots+E_{m-1}\frac{\diff}{\diff{t}}e(t)+E_me(t) \] 在经典法中，一个微分方程的解由两部分组成：齐次解和非齐次解。

齐次解 \(r_h(t)\)

求解齐次解 \(r_h(t)\) 即求解方程

Homogeneous equation 是齐次方程的英文。

\[ C_0\frac{\diff^n}{\diff{t^n}}r(t)+C_1\frac{\diff^{n-1}}{\diff{t^{n-1}}}r(t)+\cdots+C_{n-1}\frac{\diff}{\diff{t}}r(t)+C_nr(t)=0 \]

用算子符号将方程中的 \(\frac{\diff}{\diff{t}}\) 简记为 \(p\)，则方程化为 \[ C_0p^nr(t)+C_1p^{n-1}r(t)+\cdots+C_{n-1}pr(t)+C_nr(t)=0 \] 提取出特征有 \[ C_0p^n+C_1p^{n-1}+\cdots+C_{n-1}p+C_n=0 \] 该方程称为特征根方程，该方程的解称为特征根。

记特征根为 \(\lambda_k\)，则齐次微分方程的通解为 \[ r(t)=Ae^{\lambda_kt} \]

\(e^{\lambda_k t}\) 又称为模态。

（1）若特征根各不相同（无重根），那么解出的齐次解为 \[ \begin{align} r_h(t)&=A_1e^{\lambda_1 t}+A_2e^{\lambda_2 t}+\cdots+A_ne^{\lambda_n t}\\ &=\sum^n_{i=1}A_ie^{\lambda_i t} \end{align} \] （2）若有重根，例如 \(\lambda_1\) 是特征根方程的 \(k\) 阶重根，那么重根部分会使得齐次解的一部分替换为 \[ (\sum^k_{i=1}A_it^{k-i})e^{\lambda_1 t} \] \(k\) 阶重根指这个特征根有几个相同的根。

例如，求如下微分方程的齐次解 \[ \frac{\diff^3}{\diff{t^3}}r(t)+7\frac{\diff^2}{\diff{t^2}}r(t)+16\frac{\diff}{\diff{t}}r(t)+12r(t)=e(t) \] 特征方程为 \[ p^3+7p^2+16p+12=0 \] 化简得到 \[ (p+2)^2(p+3)=0 \] 求解得到 \[ \lambda_1=\lambda_2=-2,\lambda_3=-3 \] 知 \(-2\) 为二阶重根。

故齐次解为 \[ r_h(t)=(A_1t+A_2)e^{-2t}+A_3e^{-3}t \]

特解 \(r_p(t)\)

微分方程的特解 \(r_p(t)\) 与激励函数的形式有关系。

例如，求如下微分方程的特解 \[ \frac{\diff^2}{\diff{t^2}}r(t)+2\frac{\diff}{\diff{t}}r(t)+3r(t)=\frac{\diff}{\diff{t}}e(t)+e(t) \] 其中 \(e(t)=t^2\)。

代入得到激励为 \[ t^2+2t \] 选取特解函数式 \[ r_p(t)=B_1t^2+B_2t+B_3 \] 代入可解 \[ r_p(t)=\frac{1}{3}t^2+\frac{2}{9}t-\frac{10}{27} \]

注意齐次解是通解，没有初始条件无法求得系数的值，仅仅与系统本身的性质有关；但特解与外部输入有关。

初始条件求待定系数

在系统中，激励一般在 \(t=0\) 时刻加入，故当 \(t=0\) 的一组条件就是初始条件，代入可得 \[ \left\{\begin{array}{l} r(0)=A_{1}+A_{2}+\cdots+A_{n}+r_{\mathrm{p}}(0) \\ \frac{\mathrm{d}}{\mathrm{d} t} r(0)=A_{1} \alpha_{1}+A_{2} \alpha_{2}+\cdots+A_{n} \alpha_{n}+\frac{\mathrm{d}}{\mathrm{d} t} r_{\mathrm{p}}(0) \\ \quad \vdots \\ \frac{\mathrm{d}^{n-1}}{\mathrm{~d} t^{n-1}} r(0)=A_{1} \alpha_{1}^{n-1}+A_{2} \alpha_{2}^{n-1}+\cdots+A_{n}+\frac{\mathrm{d}^{n-1}}{\mathrm{~d} t^{n-1}} r_{\mathrm{p}}(0) \end{array}\right. \]

起始点的跳变

由于激励信号的作用，响应 \(r(t)\) 可能会发生跳变（如电感电流和电容电压），为区分跳变前后的状态，我们定义：

\(0_-\) 表示为激励接入之前的是瞬时；
\(0_+\) 表示为激励接入之后的是瞬时；

同时代入后的两组状态：

\(r^{(k)}(0_-)\) 称作起始状态（\(0_-\) 状态）；
\(r^{(k)}(0_+)\) 称作初始状态（\(0_+\) 状态），或导出的起始状态。

零输入响应与零状态响应

齐次解的函数特性仅依赖于系统本身，与激励信号的函数形式无关，因而称为系统的自由响应（固有响应）。

但特解的形式完全由激励函数决定，因而称为系统的强迫响应（受迫响应）。

零输入响应：没有外加激励信号的作用，只由起始状态（起始时刻储能）所产生的响应。

一般以 \(r_{zi}(t)\) 表示。（zero input 为零输入的英文）

仅字面意思可理解为不考虑任何输入对系统的作用，仅关注系统本身的性质。

零状态响应：不考虑起始时刻的系统储能的作用（起始状态为 0，或零初始条件）由系统外加激励信号所产生的响应。

一般以 \(r_{zs}(t)\) 表示。（zero state 为零状态的英文）

仅字面意思可理解为不考虑任何系统本身，仅考虑输入对系统所产生的影响。

按照上述定义，可以知道 \[ r_{zi}(t)=\sum^n_{k=1}A_{zik}e^{\lambda_k t} \] 即，零状态输入是齐次解的一部分。

其中常系数可以由 \(r^{(k)}(0_-)\) 决定，即由 \(0_-\) 状态决定。

而 \(r_{zs}(t)\) 理应是解的剩下一部分，即 \[ r_{zs}(t)=\sum^n_{k=1}A_{zsk}e^{\lambda_kt}+B(t) \] 即为自由响应的一部分与强迫相应之和。

从中我们可以得出一个结论：自由响应中的两部分，一部分由起始状态决定，另一部分由激励信号决定。

有一个附加结论：当系统无储能，零输入响应即为零。当一个系统发生跳变，则只可能影响零状态响应。

例如，求如下微分方程的自由响应、强迫响应、零输入响应和零状态响应以及完全响应。 \[ \frac{\diff}{\diff{t}}r(t)+3r(t)=3e(t) \] 其中 \(e(t)=u(t)\)，起始状态 \(r(0_-)=\frac{3}{2}\)。

这里的 \(u(t)\) 表示前文的单位阶跃信号。

由经典法可得，自由响应 \[ r_h(t)=\frac{1}{2}e^{-3t} \] 强迫响应 \[ r_p(t)=1 \] 完全响应 \[ r(t)=\frac{1}{2}e^{-3t}+1 \] 求零输入响应可得 \[ r_{zi}(t)=\frac{3}{2}e^{-3t} \] 令 \(r(0_+)=0\)，解得

不考虑起始状态的储能 \(r(0_-)\)，故没有发生跳变的情况下 \(r(0_-)=r(0_+)=0\)

\[ r_{zs}(t)=-e^{-3t}+1 \]

零状态响应的用处

由于大量的通信与电子系统的系统储能一般都为零，故只需讨论零状态响应。
零状态响应可用卷积求解。
零响应满足系统叠加性和齐次性，便于我们研究其他 LTI 系统。

冲激响应与阶跃响应

以单位冲激信号 \(\delta(t)\) 作为激励信号，系统所产生的零状态响应称为单位冲激响应（冲激响应）。

以单位阶跃信号 \(u(t)\) 作为激励信号，系统所产生的零状态响应称为单位阶跃响应（阶跃响应）。

对某个激励信号求解零状态响应，可以转化为将这个激励信号分解为无数个单位冲激信号，然后求和每个单位冲激信号的冲激响应，这是卷积求解零状态响应的基本原理。

利用了线性系统的叠加性和齐次性，显然响应可以化为冲激响应和。在这里利用卷积加权求和的特性，解得冲激响应和。

首先我们要知晓如何计算冲激响应 \(h(t)\)。

对于微分方程 \[ \newcommand{\diff}{\mathrm{d}} C_0\frac{\diff^n}{\diff{t^n}}r(t)+C_1\frac{\diff^{n-1}}{\diff{t^{n-1}}}r(t)+\cdots+C_{n-1}\frac{\diff}{\diff{t}}r(t)+C_nr(t)\\ =E_0\frac{\diff^m}{\diff{t^m}}e(t)+E_1\frac{\diff^{m-1}}{\diff{t^{m-1}}}e(t)+\cdots+E_{m-1}\frac{\diff}{\diff{t}}e(t)+E_me(t) \] 代入 \(e(t)=\delta(t)\)，可得右式可能为冲激函数、冲击偶函数及其各阶导数。

由于要使左右式子平衡，故 \(h(t)\) 与 \(m,n\) 的相对大小相关。

\(m,n\) 的相对大小可以评估为左右式导数阶数。

一般的系统都会有 \(n>m\)，此时 \(h(t)\) 中不包含 \(\delta(t)\) 及其各阶导数，简单来说，\(h(t)\) 与齐次解形式相同 \[ h(t)=\sum^n_{i=1}A_ie^{\lambda_i t} \] 对系数的求解可以直接使用系数匹配法。

一般来说，如果 \(n=m+1\)，即左式是二阶微分方程，右式是一阶微分方程，则设 \[ h(t)=(\sum^n_{i=1}A_ie^{\lambda_i t})u(t) \] 因为 \(h(t)\) 不包含 \(\delta(t)\) 及其各阶导数，但是方程两式又出现相等，那么 \(h(t)\) 只可能包含 \(\delta(t)\) 的各阶积分，在这里 \(u(t)\) 是 \(\delta(t)\) 的一阶积分，即单位阶跃函数。

同理，如果 \(n=m+2\)，那么设 \[ h(t)=(\sum^n_{i=1}A_ie^{\lambda_i t})R(t) \] 在这里，\(R(t)\) 是 \(\delta(t)\) 的二阶积分，即单位斜变函数。

例如，求解如下微分方程的冲激响应 \(h(t)\) \[ \frac{\diff^2}{\diff{t^2}}r(t)+4\frac{\diff}{\diff{t}}r(t)+3r(t)=\frac{\diff}{\diff{t}}e(t)+2e(t) \] 利用经典法可得 \[ r_h(t)=A_1e^{-t}+A_2e^{-3t} \] 故设 \[ h(t)=(A_1e^{-t}+A_2e^{-3t})u(t) \] 代入后作系数的一一对应，可求解得到 \[ A_1=A_2=\frac{1}{2} \] 故冲激响应为 \[ h(t)=\frac{1}{2}(e^{-t}+e^{-3t})u(t) \] 冲激响应表

如果 \(n\leq m\)，很显然 \(h(t)\) 包含 \(\delta(t)\) 及其导数，例如当 \(n=m\) 时，可设 \[ h(t)=(\sum^n_{i=1}A_ie^{\lambda_i t})u(t)+B\delta(t) \] 但此种情况更推荐选择求阶跃响应 \(g(t)\)，可设 \[ g(t)=(\sum^n_{i=1}A_ie^{\lambda_i t})u(t) \]

求解阶跃响应 \(g(t)\) 同理。

且在 LTI 系统中阶跃响应与冲激响应的关系为 \[ g(t)=\int^t_{-\infty}h(\tau)\diff{\tau} \] 需要注意的重点是，冲激响应与阶跃响应完全由系统本身决定，与外界因素无关。

同时由于冲激函数和阶跃函数的关联性，冲激响应与阶跃响应也有一定的关联性，这里可以用 LTI 系统的微分性。

卷积

由单位冲激信号的特性，我们知道 \[ f(t_0)=\int^{\infty}_{-\infty}f(t)\delta(t-t_0)\diff{t}=f(t_0)\delta(t-t_0)\Delta{t_0} \] 故对于任意处的激励信号，可以表示为冲激信号，即 \[ e(t_k)=e(t_k)\delta(t-t_k)\Delta{t_k} \] 显然 \(e(t_k)\Delta{t_k}\) 在此式中为常数，对于此冲激信号有冲激响应为 \[ e(t_k)\Delta{t_k}\cdot h(t-t_k) \] 对该冲激响应求和 \[ \sum^n_{k=1}e(t_k)\Delta{t_k}\cdot h(t-t_k) \] 当 \(\Delta t_k\to 0\) 时，即可写为积分形式 \[ r(t)=\int^t_0 e(\tau)h(t-\tau)\diff{\tau} \]

这里的 \(r(t)\) 的实际意义是零状态响应，因为是冲激响应之和。

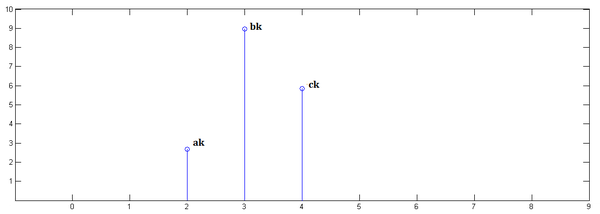
例如，有如下一个激励信号（以离散信号为例）

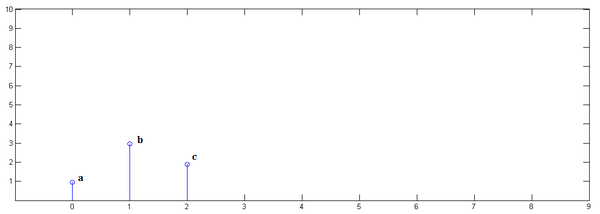
对于一个系统的冲激响应如下（以离散响应为例）

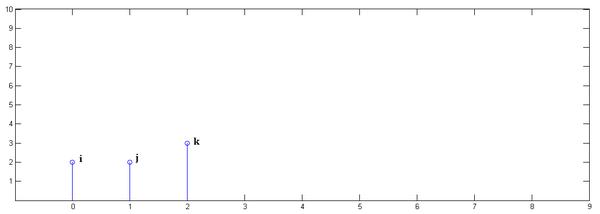
显然对于每一个激励可以用冲激函数简单表示为 \[ e_0=e_0\delta(t-0)=a\cdot \delta(t-0)\\ e_1=e_1\delta(t-1)=b\cdot \delta(t-1)\\ e_2=e_2\delta(t-2)=c\cdot \delta(t-2) \] 那么对于每个激励所造成的响应可以简单表示为 \[ r_0=e_0h(t-0)=a\cdot h(t-0)\\ r_1=e_1h(t-1)=b\cdot h(t-1)\\ r_2=e_2h(t-2)=c\cdot h(t-2) \] 其中，\(h(t-0),h(t-1),h(t-2)\) 分别代表冲激函数移位的结果。

我们可以得到每个激励的响应 \(r_0,r_1,r_2\) 如下

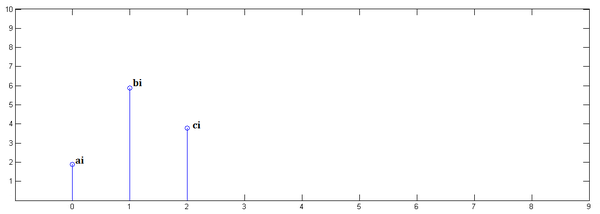
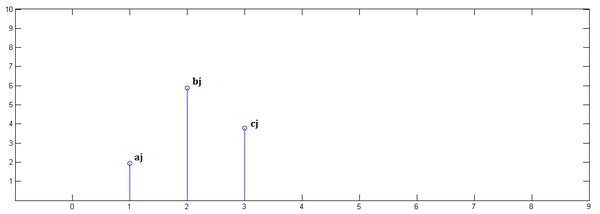
最后根据叠加原理，得到最终的响应

在信号与系统中，我们把这种信号的叠加积分运算（或离散求和运算）称作卷积。

卷积的定义式如下 \[ f(t)*g(t)=\int^{\infty}_{-\infty}f(\tau)g(t-\tau)\diff{\tau} \] 其中 \(*\) 代表对两个函数求卷积。

根据上面的例子，可以知道卷积的运算实际上是用 \(f(t)\) 的每个值倍乘 \(g(t)\) 函数，同时移位到每个值对应的位置上后，进行求和，积分仅是连续求和。

例如，系统微分方程如下，\(e(t)=u(t)-u(t-t_0)\)，求解冲激响应 \(h(t)\) 和零状态响应。 \[ \frac{\diff}{\diff{t}}r(t)+3r(t)=e(t) \] 易求 \[ h(t)=e^{-3t}u(t) \] 则零状态响应 \[ \begin{align} r(t)&=\int^t_0 [u(\tau)-u(\tau-t_0)]e^{-3(t-\tau)}\diff{\tau}\\ &=u(t)\int^t_0 e^{-3(t-\tau)}\diff{\tau}+u(t-t_0)\int^t_{t_0} e^{-3(t-\tau)}\diff{\tau}\\ &=\frac{1}{3}(1-e^{-3t})u(t)+\frac{1}{3}[1-e^{-3(t-t_0)}]u(t-t_0) \end{align} \]

这里运用了卷积的方法求零状态响应，其中第一步到第二步用了积分的加法性质，\(u(t)\) 是单位阶跃函数，故 \(u(t-t_0)\) 使得积分上下限改变。

卷积的性质

交换律

\[ f(t)*g(t)=g(t)*f(t) \]

分配律

\[ f(t)*[g(t)+h(t)]=f(t)*g(t)+f(t)*h(t) \]

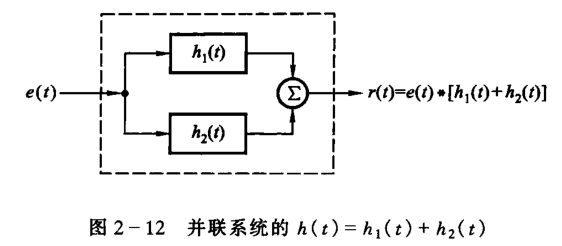
应用于并联系统的分析，两系统各自的冲激响应之和等于并联系统的冲激响应。

结合律

\[ [f(t)*g(t)]*h(t)=f(t)*[g(t)*h(t)] \]

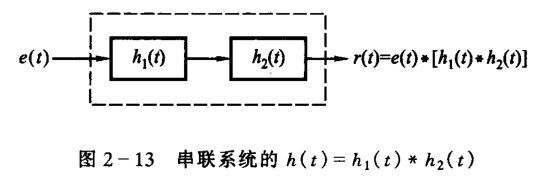
应用于串联系统的分析，两系统各自的冲激响应的卷积等于并联系统的冲激响应。

微分

\[ \begin{align} \frac{\diff}{\diff{t}}[f(t)*g(t)] &=f(t)*\frac{\diff}{\diff{t}}g(t)\\ &=\frac{\diff}{\diff{t}}f(t)*g(t) \end{align} \]

高阶微分同理，保证各自微分阶数和为总微分阶数即可。

积分

\[ \begin{align} \int[f(t)*g(t)]\diff{t} &=\int f(t)\diff{t}\cdot g(t)\\ &=f(t)\cdot \int g(t)\diff{t} \end{align} \]

高阶积分同理，保证各自积分阶数和为总积分阶数即可。

与冲激函数的卷积

\[ f(t)*\delta(t-t_0)=f(t-t_0) \]

利用微分性质，与冲激偶函数的卷积为 \[ f(t)*\delta'(t-t_0)=f'(t-t_0) \] 利用积分性质，与单位阶跃函数的卷积 \[ f(t)*u(t)=\int f(t)\diff{t} \] 推广到一般情况有 \[ f(t)*\delta^{(k)}(t-t_0)=f^{(k)}(t-t_0) \] 即，微分积分的传递性。

即卷积满足线性运算。

用算子表示微分方程注意事项

在经典法中提过，使用 \(p\) 表示微分 \[ p=\frac{\diff}{\diff{t}} \] 用 \(\frac{1}{p}\) 表示积分 \[ \frac{1}{p}=\int\diff{t} \] 但需要注意的是，化为符号算子表示微分方程只为简化表示和运算，并非真正满足多项式运算的算子。

\(p\) 多项式可以进行因式分解和同类项合并；
不可任意消去等式两端的 \(p\)；
微分积分次序不可交换。

传输算子

在开头提过，微分方程可写成 \[ C_0p^nr(t)+C_1p^{n-1}r(t)+\cdots+C_{n-1}pr(t)+C_nr(t)=E_0p^me(t)+E_1p^{m-1}e(t)+\cdots+E_{m-1}pe(t)+E_me(t) \] 定义 \[ D(p)=C_0p^n+C_1p^{n-1}+\cdots+C_{n-1}p+C_n\\ N(p)=E_0p^m+E_1p^{m-1}+\cdots+E_{m-1}p+E_m \] 那么原方程可化为 \[ r(t)=\frac{N(p)}{D(p)}e(t) \] 我们定义 \[ H(p)=\frac{N(p)}{D(p)} \] 称作系统传输算子。

自动控制原理中称作传递函数。

传输算子完整地建立了描述系统的顺序模型，一些有用的系统特性可以通过对 \(H(p)\) 分析而得出。

跟拉氏变换法形式一致。