信号与系统笔记

信号与系统

简介

信号的分类

确定性信号与随机性信号

• 确定性信号（规则信号）：信号可以被表示为一个确定的时间函数 \(f(t)\)，但确定性信号也代表着我们没办法获得任何新的信息，因为它的未来是既定的。
• 随机性信号：某一时刻的信号是无法确定的，或者称作未来是不确定的，这代表着它可以传递新的信息。

周期信号与非周期信号

一个确定性信号又被分为周期信号与非周期信号，因为这将帮助我们简化研究。

• 周期信号：即时间函数存在周期，写作 \(f(t)=f(t+nT),n\in Z\)，例如 \(f(t)=\sin{t}\) 是典型的正弦信号。
• 非周期信号：一般为了方便研究，通常会将非周期信号当作 \(T\to \infty\) 的一个周期信号。

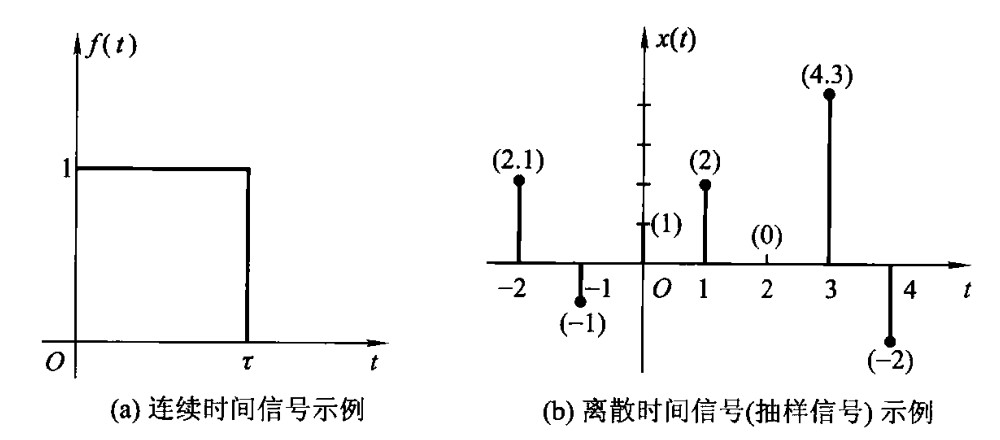
连续时间信号与离散时间信号

• 连续时间信号：除了有限个间断点以外的在任意时刻都有确切函数值的信号称作连续信号。
• 离散时间信号：时间上是离散的，只在某些不连续的瞬时点上存在函数值，其他时间上没有定的信号称作离散信号。

需要注意的是，连续信号并非是连续函数，仅仅是区别于离散信号之称。

一般情况下，用 \(t\) 表示连续时间变量；用 \(n\) 表示离散时间变量

连续时间信号与离散时间信号示例

一维信号与多维信号

由于确定性信号是一个确定的函数表达式，所以可以被分为单变量函数和多变量函数。

• 一维信号：单变量函数，例如语音信号中声压随时间变化的函数。
• 多维信号：多变量函数，例如图像信号中光强与坐标的函数。

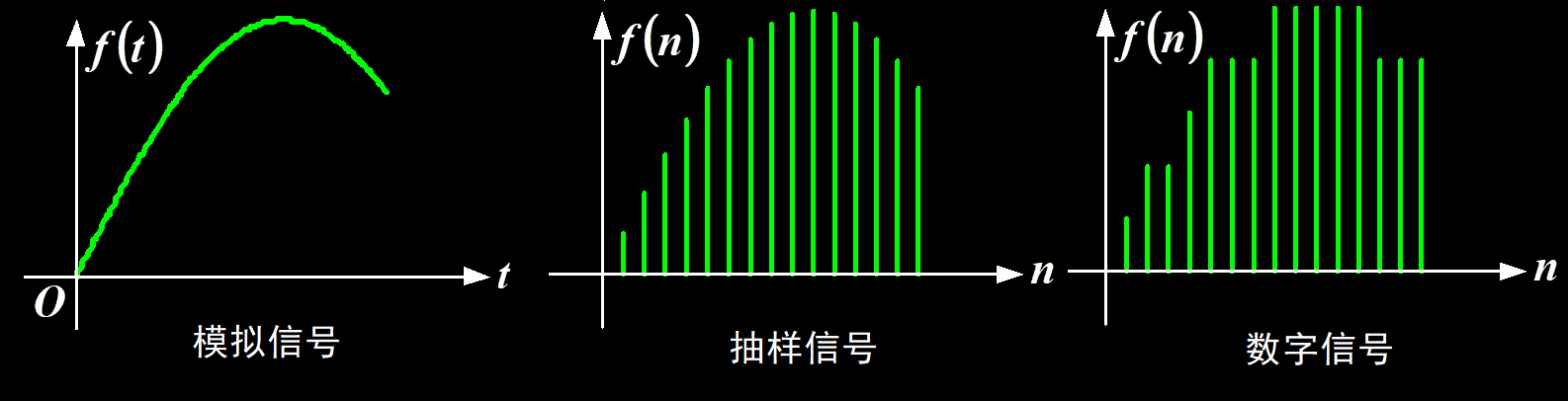
模拟信号，抽样信号与数字信号

• 模拟信号：一般是真实世界中的连续信号，例如语音信号
• 抽样信号：时间是离散的，但幅值是连续的（有无限个幅值），一般是通过抽样函数抽样后得到的信号
• 数字信号：一般是方便传输和计算机运算的信号，时间和幅值均是离散的（幅值为有限个，例如普通单片机中的数字信号仅有 \(0\) 和 \(5\symbf{V}\)）

模拟信号和抽样信号和数字信号示例

典型确定性信号

为方便研究，一般我们仅考虑信号中 \(t\geq 0\) 的部分。

指数信号

指数信号的表达式为 \[ f(t)=Ke^{at} \] 其中 \(a\) 为实数，由函数特性可知：

• 当 \(a>0\) 时，信号将随时间增长；
• 当 \(a<0\) 时，信号将随时间衰减；
• 当 \(a=0\) 时，信号将不随时间变化，退化为 \(f(t)=K\)，即直流信号。

常数 \(K\) 表示指数信号的初始状态（即 \(t=0\) 时的初始值）。

指数信号波形

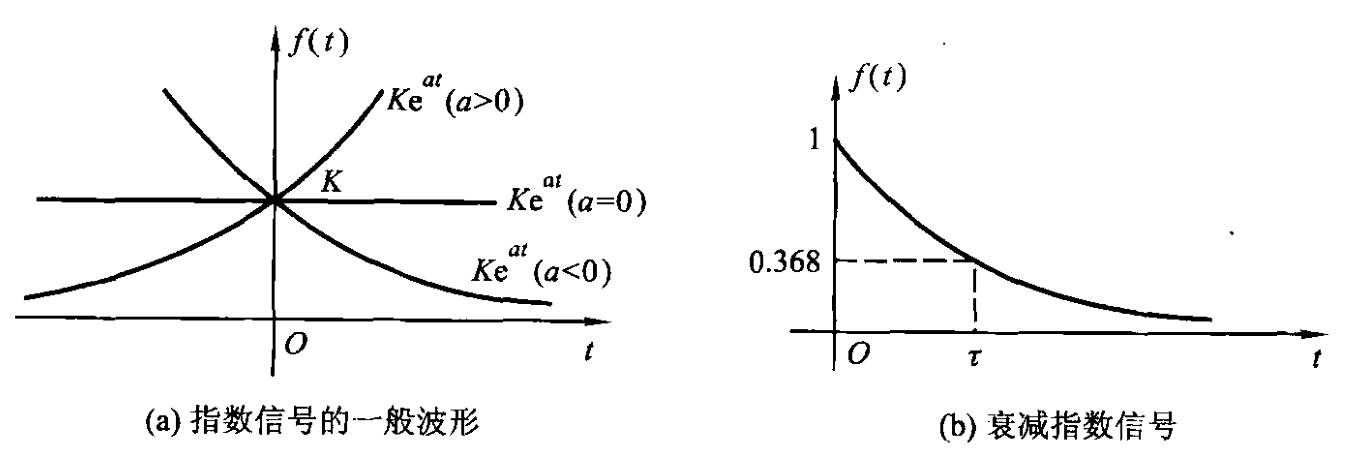
由于 \(a\) 的绝对值的大小反映了信号增长或衰减的速率（快慢），故通常记 \[ \tau=\frac{1}{|a|} \] 称作时间常数，这个值越大代表指数信号增长或衰减的速率越慢。

现实生活中通常遇到的是衰减指数信号（如负反馈系统中特别常见），记作 \[ f(t)=\begin{cases} Ke^{-\frac{t}{\tau}} & t\geq 0\\ 0 & t<0 \end{cases} \]

主要是喜欢它对时间的微分和积分仍是指数信号的性质。

正弦信号

正弦信号与余弦信号不作区分（由于仅相差 \(\frac{\pi}{2}\) 个相位），仅讨论正弦信号，表达式为 \[ f(t)=K\sin{(\omega t+\theta)} \] 其中 \(K\) 为振幅，\(\omega\) 为角频率，\(\theta\) 为初相位。

正弦信号

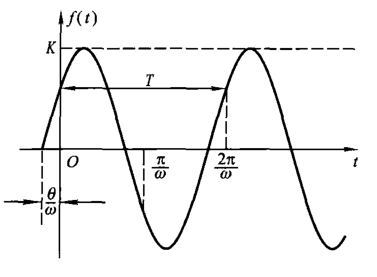
正弦信号是周期信号，满足 \[ T=\frac{2\pi}{\omega}=\frac{1}{f} \] 其中，\(f\) 为频率，表示正弦信号震荡的快慢。

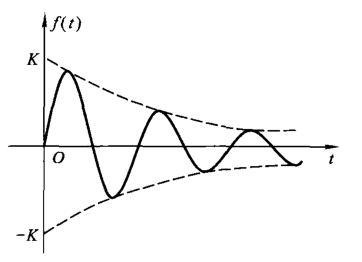
实际的正弦震荡信号可能按指数规律衰减，一般乘以指数信号表达，其表达式为 \[ f(t)=\begin{cases} Ke^{-\frac{t}{\tau}}\sin{(\omega t+\theta)} & t\geq 0\\ 0 & t<0 \end{cases} \]

同时需要注意的是，在复分析中会使用复指数信号表示正弦信号，即 \[ \newcommand{\j}{\mathrm{j}} \sin{(\omega t)}=\frac{1}{2\j}(e^{\j\omega t}-e^{-\j\omega t})\\ \cos{(\omega t)}=\frac{1}{2}(e^{\j\omega t}+e^{-\j\omega t}) \]

同样的，正弦信号的微分和积分结果是同频率的正弦信号

复指数信号

复指数信号的表达式为 \[ f(t)=Ke^{st} \] 其中 \[ s=\sigma+\j\omega \] 借助欧拉公式可以展开复指数信号： \[ Ke^{st}=Ke^{\sigma t}\cos{(\omega t)}+\j Ke^{\sigma t}\sin{(\omega t)} \] 即复指数信号由两部分信号组成：实部的余弦信号，虚部的正弦信号。

其中 \(\sigma\) 表示了振幅随时间变化的快慢，且

• 当 \(\sigma >0\) 时，正弦信号和余弦信号是增幅振荡；

• 当 \(\sigma <0\) 时，正弦信号和余弦信号是衰减振荡；

• 当 \(\sigma =0\) 时，正弦信号和余弦信号是等幅振荡。

• 当 \(\sigma=0,\omega=0\)，即 \(s=0\) 时，此时退化为直流信号，即 \(f(t)=K\)。

一般用作简化分析。

抽样信号（\(\newcommand{\Sa}{\mathop{\mathrm{Sa}}}\Sa{(t)}\)）

抽样信号一般记作 \(\Sa(t)\)，表达式为 \[ \Sa{(t)}=\frac{\sin{t}}{t} \] 可以知道其为偶函数，图像如下

抽样信号图像

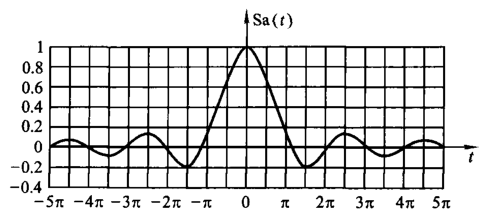
其中可以证明得到如下性质 \[ \newcommand{\diff}{\mathrm{d}} \begin{align} \lim_{t\to 0}\Sa{(t)}&=1\\ \lim_{t\to \infty}\Sa{(t)}&=0\\ \int^{\infty}_0\Sa{(t)}\diff{t}&=\frac{\pi}{2}\\ \int^{\infty}_{\infty}\Sa{(t)}\diff{t}&=\pi \end{align} \] 与 \(\Sa(t)\) 相似的有 \[ \newcommand{\sinc}{\mathop{\mathrm{sinc}}} \sinc{t}=\frac{\sin{\pi t}}{\pi t} \]

需要注意的是， \[ \Sa{(\frac{n}{2}\pi)}= \begin{cases} \pm1,n=2k+1\\ \delta(t),n=2k \end{cases} \]

有些书中，也把两种符号混用。

由于现实中无法创造真正的冲激函数，而创造 \(\Sa{(t)}\) 却是容易的，故我们可以使得其频率特别大而接近于冲激函数以便采样。

钟形信号（高斯函数）

钟形信号的表达式为 \[ f(t)=Ee^{-(\frac{t}{\tau})^2} \]

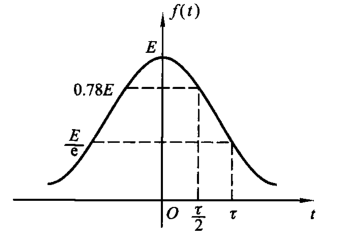
可以得知 \[ f(\frac{\tau}{2})=Ee^{-\frac{1}{4}}\approx 0.78E \] 即 \(\tau\) 为信号从 \(E\) 衰减到 \(0.78E\) 时所占据的时间宽度，也称作带宽。

钟形信号在随机信号分析中占重要地位。

信号的运算

移位

数学表达式为 \(f(t)\to f(t-t_0)\)，其中 \(t_0\) 为信号位移量。

信号的位移

• 当 \(t_0>0\) 时，信号向右位移，又称信号滞后；
• 当 \(t_0<0\) 时，信号向左位移，又称信号超前；

比如说同一个波源发射的波信号通过同一种介质传播在不同位置的波信号相对于波源处的波信号就会出现滞后现象，这与传播的时间差（或波程）有关系。

反褶

数学表达式为 \(f(t)\to f(-t)\)，即信号的未来与过去发生了交换。

信号的反褶

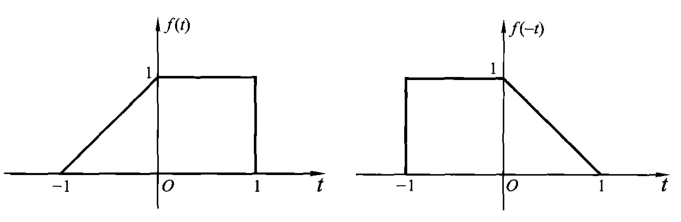
实际物理元器件无法做到反褶，仅能在数字处理中做到相应的概念。

尺度变换

尺度变换又称作尺度倍乘，数学表达式为 \(f(t)\to f(at)\)，其中 \(a\) 为尺度。

• 当 \(a>1\) 时，信号将被压缩，即保持信号的时间缩短了；
• 当 \(a<1\) 时，信号将被扩展，即保持信号的时间增长了。

信号的尺度变换

微分

即信号对时间 \(t\) 求导数： \[ f'(t)=\frac{\diff}{\diff{t}}f(t) \]

在实际物理元器件中，可以使用电感电路求电信号的微分。

可见微分可以突出信号的变化部分。

如果是黑白图像信号，那么微分运算可以突出它的边缘轮廓，这也是图像处理中常用的手法。

微分运算

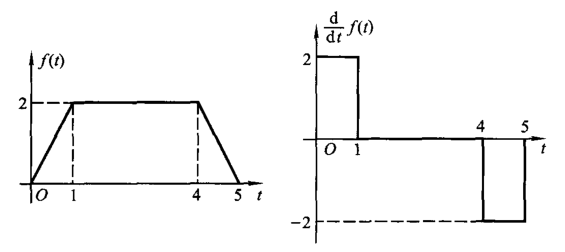
需要注意的是，如果对阶跃信号求微分将得到冲激信号。

积分

即信号对时间 \(t\) 求积分： \[ \int^t_{-\infty}f(\tau)\diff{\tau} \]

在实际物理元器件中，可以使用电容电路求电信号的积分。

可见微分可以使得信号的变化部分变得平滑。

如果是黑白图像信号，那么积分运算可以削弱图像中的噪声，这也是图像处理中常用的手法。

积分运算

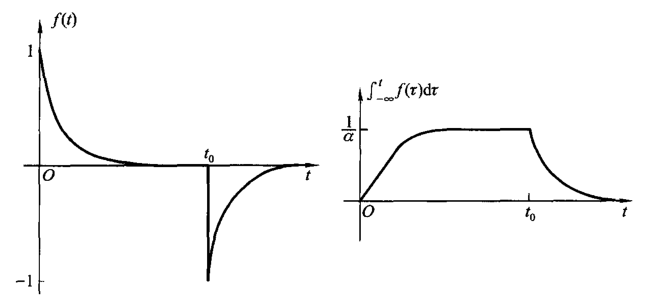
需要注意的是，如果对冲激信号求积分将得到阶跃信号。

相加与相乘

相加与相乘

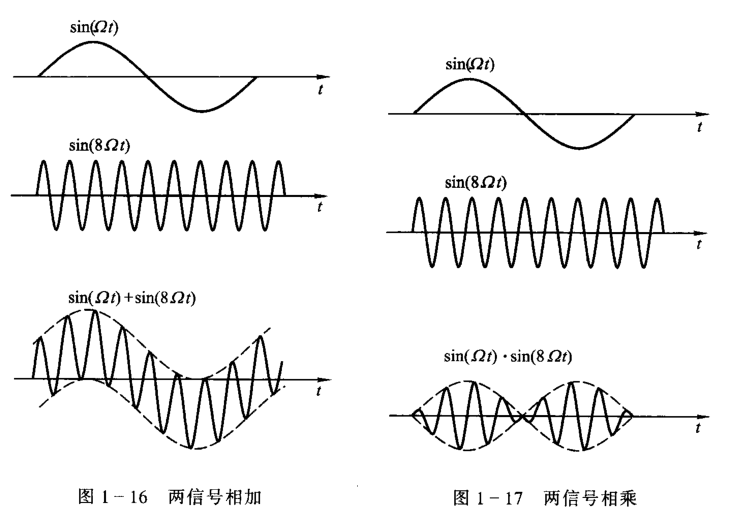
需要说明的是，在通信系统的调制、解调等过程中，将经常遇到两信号相乘运算。

经典奇异信号

奇异信号即函数本身有不连续点（跳变点）或其导数与积分有不连续点的信号。

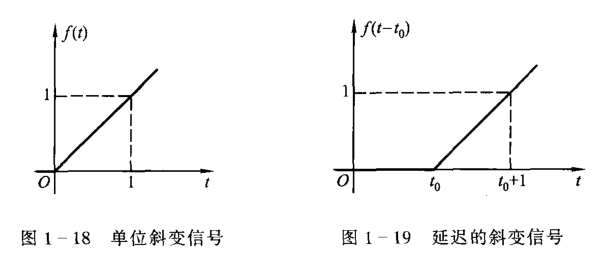
单位斜变信号

即信号的函数表达式是正比例函数的信号，表达式为 \[ R(t)=\begin{cases} t & t\geq0\\ 0 & t<0 \end{cases} \] 若将起始点移位至 \(t_0\) 即写为 \[ R(t-t_0)=\begin{cases} t-t_0 & t\geq t_0\\ 0 & t<t_0 \end{cases} \]

单位斜变信号记作 \(R(t)\)。

斜变信号

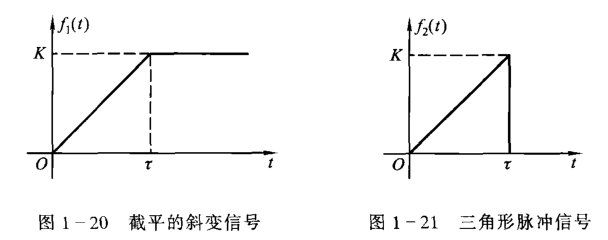
实际应用中会常遇到截平的斜变信号，在时间 \(\tau\) 后信号波形被切平，表达式为 \[ f_1(t)=\begin{cases} \frac{K}{\tau}t & t < \tau\\ K & t\geq \tau \end{cases} \] 通常三角形脉冲信号用斜变信号表示： \[ f_1(t)=\begin{cases} \frac{K}{\tau}t & t\leq \tau\\ 0 & t> \tau \end{cases} \]

单位阶跃信号

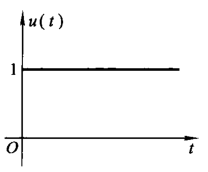
单位阶跃信号的表达式为 \[ u(t)=\begin{cases} 0 & t<0\\ 1 & t>0 \end{cases} \]

一般记单位阶跃信号为 \(u(t)\)。

跳变点 \(t=0\) 处无定义，为方便计算一般规定为 \(u(0)=\frac{1}{2}\)。

物理背景是在 \(t=0\) 时刻对某一电路接入单位电源（直流电压源或直流电流源），并且无限持续下去。

单位阶跃信号

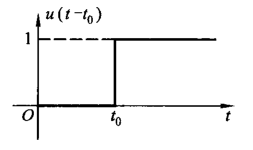
如果存在延时，可以表示为 \[ u(t-t_0)=\begin{cases} 0 & t<t_0\\ 1 & t>t_0 \end{cases} \]

可以注意到，单位斜变信号的微分就是单位阶跃信号。

通常用单位阶跃信号来表示矩形脉冲信号，即写作 \[ R_T(t)=u(t)-u(t-T) \] 表示为宽度为 \(T\)，出现在 \([0,T]\) 的一个矩形脉冲信号。 \[ G_T(t)=u(t+\frac{T}{2})-u(t-\frac{T}{2}) \] 表示为带宽为 \(T\)，出现在 \([-\frac{T}{2},\frac{T}{2}]\) 的一个矩形脉冲信号（也称作窗函数）。

矩形脉冲信号

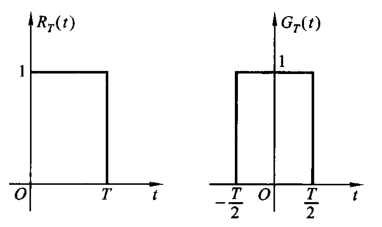
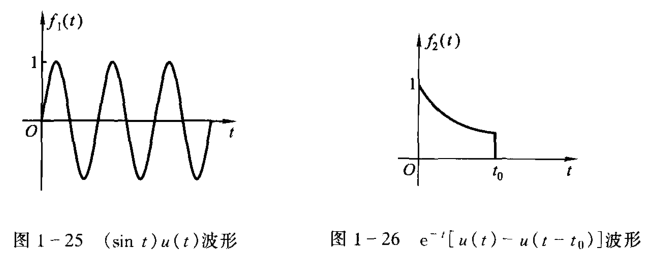
一般我们会用来在数学上抽样其他信号，例如说 \[ f_1(t)=(\sin{t})u(t) \] 表示为抽样正弦信号 \(\sin{t}\) 中 \(t\geq 0\) 的部分。

或者 \[ f_2(t)=e^{-t}[u(t)-u(t-t_0)] \] 表示为抽样指数信号 \(e^{-t}\) 中 \(0\leq t\leq t_0\) 的部分。

单位阶跃信号的抽样性

符号函数也可以用单位阶跃信号来表示： \[ \mathrm{sgn}(t)=\begin{cases} 1 & t>0\\ -1 & t<0 \end{cases} =2u(t)-1 \]

单位冲激信号

某些物理现象需要使用一个时间极短但取值极大的函数模型来描述，例如力学中的瞬时冲击力，数字通信中的抽样脉冲等。

单位冲激信号的表达式（用矩形脉冲信号定义）为 \[ \delta(t)=\lim _{\tau \rightarrow 0} \frac{1}{\tau}\left[u\left(t+\frac{\tau}{2}\right)-u\left(t-\frac{\tau}{2}\right)\right] \] 其冲激值（峰值）为 1。

也可以使用其他脉冲定义：

单位冲激信号的其他表达式

冲激函数演变图

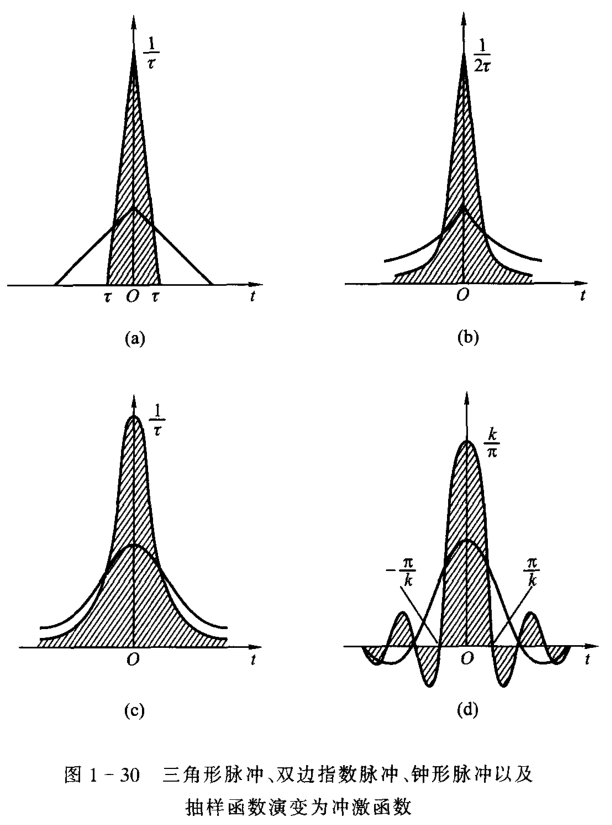
狄拉克给出单位冲激函数的另一种定义： \[ \begin{cases} \displaystyle\int^{\infty}_{-\infty}\delta(t)\diff{t}=1 & t=0\\ \delta(t)=0 & t\neq0 \end{cases} \] 故也称单位冲激函数为狄拉克函数。

描述 \(t=t_0\) 处的冲激时，可使用如下定义： \[ \begin{cases} \displaystyle\int^{\infty}_{-\infty}\delta(t-t_0)\diff{t}=1 & t=t_0\\ \delta(t-t_0)=0 & t\neq t_0 \end{cases} \]

可以发现单位冲激信号实际上为离散信号。

单位冲激信号有以下性质： \[ \int^{\infty}_{-\infty}\delta(t)f(t)\diff{t}=\int^{\infty}_{-\infty}\delta(t)f(0)\diff{t}=f(0)\int^{\infty}_{-\infty}\delta(t)\diff{t}=f(0) \] 即采样结果为冲激处的函数值。

类似地，对于延迟的单位冲激信号有 \[ \int^{\infty}_{-\infty}\delta(t-t_0)f(t)\diff{t}=\int^{\infty}_{-\infty}\delta(t-t_0)f(t_0)\diff{t}=f(t_0) \] 故单位冲激信号具有采样特性（或称筛选特性）。

单位冲激信号是偶函数。（不给予证明）

单位冲激信号的积分是单位阶跃信号： \[ u(t)=\int^t_{-\infty}\delta(\tau)\diff(\tau) \] 同理，单位阶跃信号的微分是单位冲激信号： \[ \frac{\diff}{\diff{t}}u(t)=\delta(t) \]

由积分性质可以知道，如果给予一个冲激电流信号，那么就可以使得电容两端电压发生跳变；

由微分性质可以知道，如果给予一个冲激电压信号，那么就可以使得电感两端电流发生跳变。

冲激偶信号

冲激信号的微分（阶跃信号的二阶导数）将会呈现正、负两种极性的一对冲激，称为冲激偶信号，表示为 \(\delta'(t)\)。

冲激偶的形成

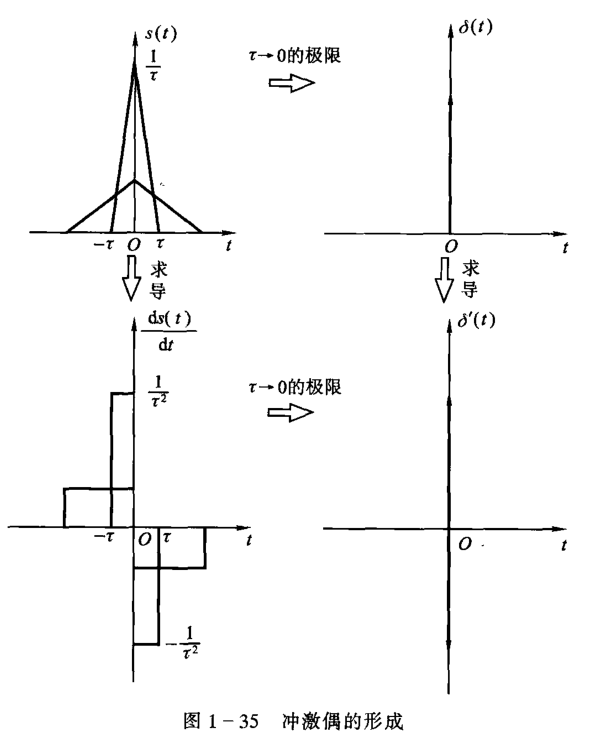
冲激偶的一个重要性质为 \[ \int^{\infty}_{-\infty}\delta'(t)f(t)\diff{t}=-f'(0) \] 或者是 \[ \int^{\infty}_{-\infty}\delta'(t-t_0)f(t)\diff{t}=-f'(t_0) \] 另一个性质是 \[ \int^{\infty}_{-\infty}\delta'(t)\diff{t}=0 \]

总结

可以发现从单位斜变信号到单位阶跃信号到单位冲激信号再到冲激偶信号是一步一步微分的结果，反之也是一步一步积分的结果，其中单位冲激信号也是之后方便采样信号的最重要的函数。

信号的分解

为方便研究信号传输和信号处理的问题，往往将一些信号分解为比较简单的或比较基本的信号分量之和。

直流分量与交流分量

信号平均值即为信号的直流分量；交流分量即为原信号去掉直流分量。

表达式为 \[ f(t)=f_D+f_A(t) \]

Direct-current 是直流的英文；Alternating-current 是交流的英文。

其中 \(f_D\) 为直流分量，\(f_A(t)\) 为交流分量。

需要知道 \(f_Df_A(t)\) 在对称区间上的积分为 0。

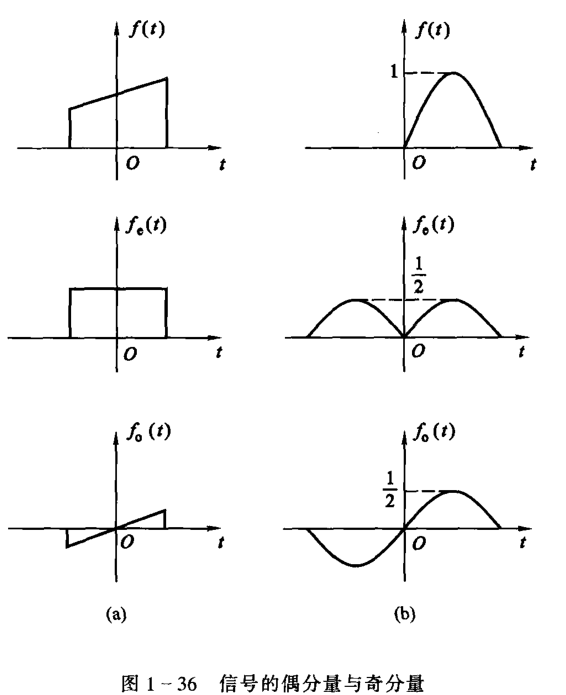
偶分量与奇分量

偶分量定义为 \[ f_e(t)=f_e(-t) \] 奇分量定义为 \[ f_o(t)=-f_o(-t) \]

even 是偶数的英文；odd 是 奇数的英文。

由于任何信号都可以写成 \[ \begin{align} f(t)&=\frac{1}{2}[f(t)+f(t)+f(-t)-f(-t)]\\ &=\frac{1}{2}[f(t)+f(-t)]+\frac{1}{2}[f(t)-f(-t)]\\ &=\frac{1}{2}f_e(t)+\frac{1}{2}f_o(t) \end{align} \] 即 \[ f_e(t)=\frac{1}{2}[f(t)+f(-t)]\\ f_o(t)=\frac{1}{2}[f(t)-f(-t)] \]

脉冲分量

一个信号可近似分解为许多脉冲分量之和。

主要的方式是将信号分解为冲激信号的叠加。

即写作 \[ f(t_0)=\int^{\infty}_{-\infty}f(t)\delta(t-t_0)\diff{t} \]

实部分量与虚部分量

主要是复分析中常采用的方式，采用共轭分解的方法。

已知 \[ f(t)=f_r(t)+\j f_i(t) \] 那么它的共轭复函数写作 \[ f^*(t)=f_r(t)-\j f_i(t) \]

real 是实数的英文；image 是虚数的英文。

那么 \[ f_r(t)=\frac{1}{2}[f(t)+f^*(t)]\\ f_i(t)=\frac{1}{2\j}[f(t)-f^*(t)] \] 且 \[ |f(t)|^2=f(t)f^*(t)=f_r^2(t)+f_i^2(t) \] 虽然现实中的信号都是实信号，但复分析可以很好的帮助我们简化信号的分析。

正交函数分量

用正交函数集来表示一个信号，那么信号分量也是相互正交的。

例如常常用正弦信号与余弦信号的叠加来表示一个矩形脉冲。

主要采用的数学工具是傅里叶级数和傅里叶展开。

系统模型

时域运算的基本元件

加法器

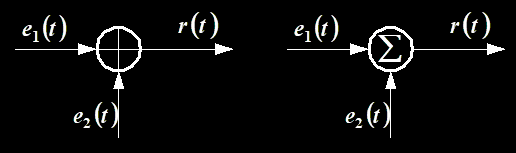\[ r(t)=e_1(t)+e_2(t) \]

encourage 是激励的英文；response 是响应的英文。

倍乘器

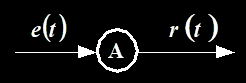\[ r(t)=Ae(t) \]

微分器

\[ r(t)=\frac{\diff}{\diff{t}}e(t) \]

积分器

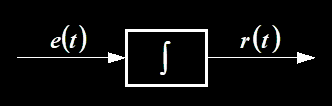\[ r(t)=\int e(t) \]

线性时不变系统

线性时不变系统即 Linear Time - Invariant，缩写为 LTI，简称 LTI 系统。

线性时不变系统具有以下一些基本特性。

叠加性与均匀性

线性系统的叠加性与均匀性

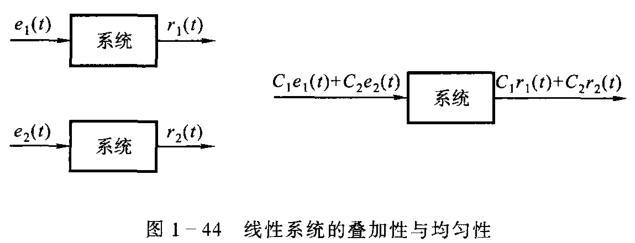
满足叠加定理，即 \[ C_1e_1(t)+C_2e_2(t)=C_1r_1(t)+C_2r_2(t) \]

时不变特性

系统响应与激励施加于系统的时刻无关。

即如果激励为 \(e(t-t_0)\)，那么响应也会相应的变为 \(r(t-t_0)\)。

微分特性

即激励为 \(\frac{\diff{e(t)}}{\diff{t}}\)，那么响应也会相应的变为 \(\frac{\diff{r(t)}}{\diff{t}}\)。

以上三个特性可以总结为，激励信号的运算也会相应作用于响应信号。

因果性

响应只与激励发生的时刻及时刻之前有关，便称为因果系统。

或者说，激励是产生响应的原因，响应式激励引起的结果，这种特性称为因果性。

例如系统模型为 \[ r_1(t)=e_1(t-1) \] 可以发现响应信号是滞后于激励信号的，故该系统是因果系统。

如果 \[ r_2(t)=e_2(t+1) \] 可以发现响应信号是超前于激励信号的，故该系统是非因果系统。

实际的物理可实现系统均为因果系统。

而在 \(t=0\) 时刻接入的系统信号称为因果信号。

系统数学模型（微分方程）的建立

RLC并联电路

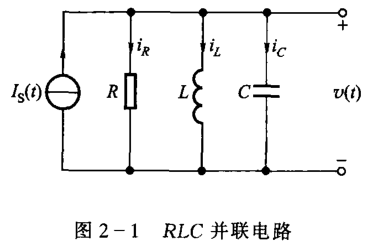
设各支路电流分别为 \(i_R(t),i_L(t),i_C(t)\)，以 \(v(t)\) 作为待求响应函数，根据元件本身的特性，可得 \[ i_R(t)=\frac{1}{R}v(t)\\ i_L(t)=\frac{1}{L}\int^t_{-\infty}v(\tau)\diff{\tau}\\ i_C(t)=C\frac{\diff}{\diff{t}}v(t) \] 根据基尔霍夫定律有 \[ i_R(t)+i_L(t)+i_C(t)=i_S(t) \] 解得 \[ C\frac{\diff^2}{\diff{t^2}}v(t)+\frac{1}{R}\frac{\diff}{\diff{t}}v(t)+\frac{1}{L}v(t)=\frac{\diff}{\diff{t}}i_S(t) \] 为一个二阶常系数微分方程。

机械位移系统

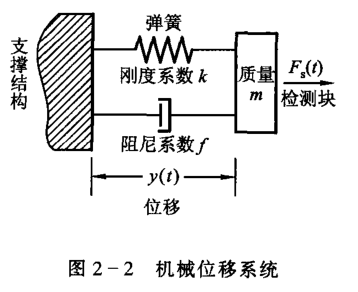
设位移速度 \(v(t)=\frac{\diff}{\diff{t}}y(t)\)，弹簧手力 \(F_k(t)\)，由胡克定律可得 \[ F_k(t)=ky(t)=k\int^t_{-\infty}v(\tau)\diff{\tau} \] 阻尼力 \[ F_f(t)=fv(t) \] 惯性力 \[ F_m(t)=m\frac{\diff}{\diff{t}}v(t) \] 根据达朗贝尔原理，系统受力应该保持平衡，有 \[ m\frac{\diff}{\diff{t}}v(t)+fv(t)+k\int^t_{-\infty}v(\tau)\diff{\tau}=F_s(t) \] 两端微分得到 \[ m\frac{\diff^2}{\diff{t^2}}v(t)+f\frac{\diff}{\diff{t}}v(t)+kv(t)=\frac{\diff}{\diff{t}}F_s(t) \] 为一个二阶常系数微分方程。

从上式可以看出，这两个系统所建立的数学模型是相似的，即使他们是性质完全不同的两个物理系统。

这是系统之间的相似性，对于完全没有接触过的系统，我们也可以通过系统的相似性来分析它。