电力电子技术笔记
电力电子技术
电力电子器件
电力电子器件最重要的参数是:能处理电功率的大小,即承受电压和电流的能力。
一般来说能承受更高的电压和更高的电流的器件是电力电子中最理想的器件。
而电力电子器件最重要的特性是开关特性:
- 导通时(通态,On-State),阻抗很小,接近于短路,管压降(Voltage Across the Tube)接近于零,而电流由外电路决定。
- 阻断时(断态,Off-State),阻抗很大,接近于断路,电流几乎为零,而管子两端电压由外电路决定。
作电路分析时,通常当作理想开关。
电力电子器件往往需要由信息电子电路来控制,在主电路和控制电路之间,需要一定的中间电路对控制电路的信号放大,这就是电力电子技术中最重要的驱动电路(Driving Circuit)。
为保证不致于因损耗散发的热量导致器件温度过高而损坏,不仅在器件封装上讲究散热设计,在其工作时一般都要安装散热器。
- 导通时器件上有一定的通态压降(On-state Voltagedrop),形成通态损耗(On-state Losses)
- 阻断时器件上有微小的断态漏电流(Leakage Current)流过,形成断态损耗(Off-state Losses)
不可控器件——电力二极管
工作特性
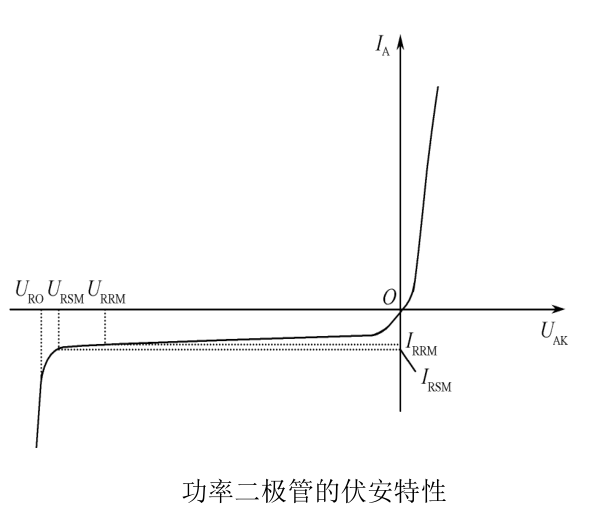
主要利用其正向导通,反向截止的工作特性,一般在整流电路中使用。
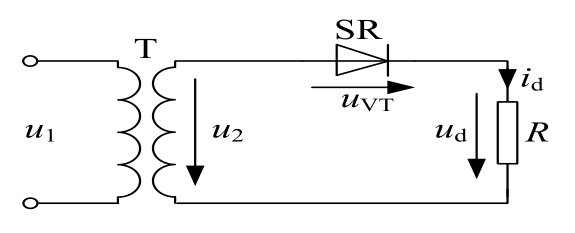
参数选型
正向平均电流,额定电流,通态平均电流,等效直流电流,即通过二极管的电流在一个周期内的平均值,计算公式为 \[ I_{FR}=\frac{1}{T}\int_0^Ti\mathrm{d}t \] 假设一个正弦半波电流的最大值为 \(I_m\),我们可以计算得到其正向平均电流为 \[ I_{FR}=\frac{1}{2\pi}\int^\pi_0I_m\sin{(\omega t)}\mathrm{d}{(\omega t)}=\frac{1}{\pi}I_{m} \] 最大允许的全周期均方根正向电流,有效值电流,按照电流的发热效应来定义,采用有效值相等的原则进行计算,额定电流应留有 1.5-2 倍的裕量。计算公式如下所示: \[ I_{Frms}=\sqrt{\frac{1}{T}\int_0^Ti^2\mathrm{d}t} \] 假设一个正弦半波电流的最大值为 \(I_m\),我们可以计算得到其最大允许的全周期均方根正向电流为 \[ I_{Frms}=\frac{1}{2\pi}\sqrt{\int^\pi_0(I_m\sin{\omega t})^2\mathrm{d}{(\omega t)}}=\frac{1}{2}I_m=\frac{2}{\pi}I_{FR}=1.57I_{FR} \] 即正弦半波的电流有效值是峰值的一半,额定电流比上电流有效值至少要为 \(1/1.57\),一般来说会向上浮动 1.5-2 倍。
比如说已知通过的电流波形有效值为 \(I_D\),那么选取效率二极管时,选取额定电流为 \(2/1.57\times I_D\) 的效率二极管。
额定 100A 的二极管理论上可以通过 157A 的电流有效值。
反向重复峰值电压,一般指电压峰值 \(U_M\),额定电压的选取一般是其的 1.5-2 倍。
国家正常电压和频率是 220V/50Hz,其中 220V 是电压有效值,需要取 \(\sqrt{2}\) 倍有效值才为峰值,即 311V,故一般额定电压的选取是 622V。
分类
- 普通二极管:普通二极管又称整流管(RD),其反向恢复时间在5μs以上,额定电流达数千安,额定电压达数千伏以上。
- 快恢复二极管:反向恢复时间在5μs以下的称为快恢复二极管(Fast Recovery Diode简称FDR)。
- 肖特基二极管:肖特基二极管是一种金属同半导体相接触形成整流特性的单极型器件,其导通压降的典型值为0.4~0.6V,而且它的反向恢复时间短,为几十纳秒。但反向耐压在200V以下。
半控型器件——晶闸管
工作特性
在二极管的正向导通,反向截止的基础上,增添一个门级电流机制,即只有门级有触发电流的情况下晶闸管才可以导通。
本质上是电力三极管器件。
参数选型
与二极管一样,额定电流应与电流有效值之比大于 1/1.57,选取裕量为 1.5-2 倍;额定电压应是电压峰值的 1.5-2 倍。
控制电路数量关系
输出电压平均值 \(U_d\) 与输出电流平均值 \(I_d\)
\[ U_d=\frac{1}{2\pi}\int^{\pi}_{\alpha}\sqrt{2}U_2\sin{(\omega t)}\mathrm{d}(\omega t)=0.45U_2\frac{1+\cos{\alpha}}{2} \]
其中,\(U_d\) 也是平均直流输出电压,\(U_2\) 是输入电压有效值。
我们可以知道当 \(\alpha=0\) 时,\(U_d=0.45U_2\),\(\alpha=\pi\) 时,\(U_d=0\),故控制角的移相范围应该是 \([0,\pi]\)。 \[ I_d=0.45\frac{U_2}{R_L}\frac{1+\cos{\alpha}}{2} \] 其中,\(R_L\) 是负载电阻。
输出电压有效值 \(U\) 与输出电流有效值 \(I\)
\[ U=\sqrt{\frac{1}{2\pi}\int^{\pi}_{\alpha}[\sqrt{2}U_2\sin{(\omega t)}]^2\mathrm{d}(\omega t)}=U_2\sqrt{\frac{1}{4\pi}\sin{2\alpha}+\frac{\pi-\alpha}{2\pi}} \]
其中,\(U_2\) 是输入电压有效值。 \[ I=\frac{U}{R_L}=\frac{U_2}{R_L}\sqrt{\frac{1}{4\pi}\sin{2\alpha}+\frac{\pi-\alpha}{2\pi}} \] 其中,\(U_2\) 是输入电压有效值,\(R_L\) 是负载电阻。
晶闸管电流有效值和变压器二次侧电流有效值
单相半波可控整流器中,有 \[ I_T=I_2=I=\frac{U_2}{R_L}\sqrt{\frac{1}{4\pi}\sin{2\alpha}+\frac{\pi-\alpha}{2\pi}} \] 其中,\(I_T\) 是晶闸管电流有效值,\(I_2\) 是输入电流。
IGBT——绝缘栅双极晶体管
具体不再阐述,本质是耐高电压耐高电流的三极管,是极其优秀的电力三极管器件。