最优化方法——理论基础
最优化方法
基本理论
引子
一个简单的函数极值问题是这样的,给予一个连续可微函数 \(f(x)\),我们想要找到它什么时候取得最小值,最小值是多少,即 \[ \min{f(x)} \] 在正常的数学学习中我们知道,想要找到一个函数的最小值,我们需要知道它的导数,和导数的导数 \[ \min{f(x)}\to f'(x)=0,f''(x)>0 \] 这是找到极小值的充要条件。
这是一个最简单的优化问题,例如说找到某个产品成本在某个区间的极小值。
但现实中往往并不会只有单一变量因素,更多的是针对多变量函数的优化问题,例如神经网络的参数优化。
例如我们想要求得 \[ \min{f(x,y,z)} \] 那么自然地想要知道这个多元函数的“导数”,“导数的导数”。
多元函数的导数矩阵
连续可微多元函数的”导数“其实就是梯度,定义为 \[ \nabla f(\mathbf{x})=\begin{pmatrix} \frac{\partial f(\mathbf{x})}{\partial x_1}, \cdots, \frac{\partial f(\mathbf{x})}{\partial x_n} \end{pmatrix}^T=D(f)^T \] 我们一般定义梯度的转置才是多元函数的导数矩阵 \(D(f)\)。
因为梯度的定义是列向量,导数矩阵是行向量。
对于连续可微的向量值函数 \(F=\begin{pmatrix}F_1,\cdots,F_m\end{pmatrix}\),其导数矩阵又称作是雅可比(jacobi)矩阵 \[ F'(x)=\begin{bmatrix} \frac{\partial F_1(\mathbf{x})}{\partial x_1}& \cdots& \frac{\partial F_1(\mathbf{x})}{\partial x_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial F_m(\mathbf{x})}{\partial x_1}& \cdots& \frac{\partial F_m(\mathbf{x})}{\partial x_n} \end{bmatrix} \] 例如向量值函数 \[ \mathbf{f}(\mathbf{x})=\begin{bmatrix} \sin{x_1}+\cos{x_2}\\ e^{2x_1+x_2}\\ 2x_1^2+x_1x_2 \end{bmatrix} \] 可以求得雅可比矩阵为 \[ \mathbf{f}'(\mathbf{x})=\begin{bmatrix} \cos{x_1}&-\sin{x_2}\\ 2e^{2x_1+x_2}&e^{2x_1+x_2}\\ 4x_1+x_2&x_1 \end{bmatrix} \] 而连续可微多元函数的“导数的导数”,也被称为海森(hessian)矩阵,定义为 \[ D^2(f)=\nabla^2f(\mathbf{x})=\begin{bmatrix} \frac{\partial^2 f(\mathbf{x})}{\partial x_1^2}&\cdots&\frac{\partial^2 f(\mathbf{x})}{\partial x_1\partial x_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial^2 f(\mathbf{x})}{\partial x_n\partial x_1}&\cdots&\frac{\partial^2 f(\mathbf{x})}{\partial x_n^2} \end{bmatrix} \] 例如函数 \[ f(x_1,x_2)=\left(x_{1} - x_{2}\right)^{2} + 4 \, x_{1} x_{2} + e^{\left(x_{1} + x_{2}\right)} \] 其海森矩阵为 \[ \nabla^2 f(x_1,x_2)=\begin{bmatrix} e^{\left(x_{1} + x_{2}\right)} + 2 & e^{\left(x_{1} + x_{2}\right)} + 2 \\ e^{\left(x_{1} + x_{2}\right)} + 2 & e^{\left(x_{1} + x_{2}\right)} + 2 \end{bmatrix} \]
泰勒公式
一元函数的泰勒展开式为 \[ f(x)=\frac{f(x_0)}{0!}+\frac{f(x_0)}{1!}(x-x_0)+\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x) \] 其中,\(R_n(x)\) 称作余项,用于表示和平衡误差。完全展开后也被称作是泰勒级数 \[ f(x)\sum^{\infin}_{k=0}\frac{f^{k}(x_0)}{k!}(x-x_0)^k \] 考虑推广到多元函数,有如下定义 \[ f(\mathbf{x})=f(\mathbf{x}_0)+\frac{D(f)}{1!}(\mathbf{x}-\mathbf{x}_0)+(\mathbf{x}-\mathbf{x}_0)^T\frac{D^2(f)}{2!}(\mathbf{x}-\mathbf{x}_0)+o(\|\mathbf{x}-\mathbf{x}_0\|)^2 \] 其中,\(o(\|\mathbf{x}-\mathbf{x}_0\|)^2\) 是二次余项,用于表示和平衡误差。
例如多元函数 \(f(\mathbf{x})=x_1e^{-x_2}+x_2+1,\mathbf{x}_0=(1,0)^T\),那么忽略三次及更高次项(展开三项)得到 \[ D(f)=\begin{bmatrix} e^{-x_2}&-x_1e^{-x_2}+1 \end{bmatrix}\newline D^2(f)=\begin{bmatrix} 0&-e^{-x_2}\\ -e^{-x_2}&x_1e^{-x_2} \end{bmatrix}\newline f(\mathbf{x})=2+\begin{bmatrix} 1&0 \end{bmatrix}\begin{bmatrix} x_1-1\\ x_2 \end{bmatrix}+\frac{1}{2}\begin{bmatrix} x_1-1&x_2 \end{bmatrix}\begin{bmatrix} 0&-1\\ -1&1 \end{bmatrix}\begin{bmatrix} x_1-1\\ x_2 \end{bmatrix}+\cdots \newline =1+x_1+x_2-x_1x_2+\frac{1}{2}x_2^2+\cdots \]
凸集与凸函数
定义集合 \(D\subset R^n\),对于其中任意两点 \(x,y\in D\),任意实数 \(\alpha\in[0,1]\),满足 \[ \alpha x+(1-\alpha)y\in D \] 我们就称集合 \(D\) 为凸集。
\(R^n\) 代表每个元素都有 \(n\) 维长度。
实际上对于元素 \(x,y\) 来说,定义公式即为直线。直观上而言,凸集就是空间中内部无洞,边界又不向内凹的一些点的集合。
一个在凸集上的多元函数,类比于一元函数的光滑。
由此推广,凸函数定义为函数图形上任意两点的线段总是位于曲线弧的上方。
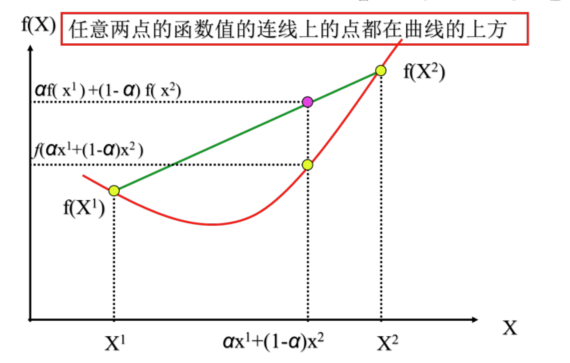
我们喜欢类似凸函数这样光滑、连续、可微的函数,显而易见地它必然有极小值,也就是说,对于一个多元凸函数,我们可以类似引子那样,找到它的极小值和极小值点。
那么现在的问题就在于,怎么去寻找一个多元凸函数。
正(负)定二次型
对于一个 \(n\) 元二次齐次函数 \[ f(x_1,x_2\cdots,x_n)=a_{11}x_1^2+a_{22}x_2^2+\cdots+a_{nn}x_n^2\newline +2a_{12}x_1x_2+2a_{13}x_1x_3+\cdots+2a_{n-1,n}x_{n-1}x_{n} \] 称作二次型,取 \(a_{ij}=a_{ji}\),那么 \(2a_{ij}x_ix_j=a_{ij}x_ix_j+a_{ji}x_jx_i\),于是可以把二次型记作 \[ f(x_1,x_2,\cdots,x_n)=\sum^n_{i,j=1}a_{ij}x_ix_j \] 同时也可以写作矩阵形式 \[ \mathbf{A}=\begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{bmatrix} x=\begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{pmatrix}\\ f(x_1,x_2,\cdots,x_n)=\mathbf{x}^T\mathbf{A}\mathbf{x} \] 其中 \(A\) 为对称矩阵,称作是二次型的矩阵。
对于二次型矩阵,我们定义,如果对于任意 \(\mathbf{x}_0\neq 0\),如果有
\(f(\mathbf{x}_0)>0\),则称 \(f\) 是正定二次型,对应的实对称矩阵 \(\mathbf{A}\) 为正定矩阵;
\(f(\mathbf{x}_0)<0\),则称 \(f\) 是负定二次型,对应的实对称矩阵 \(\mathbf{A}\) 为负定矩阵。
\(f(\mathbf{x}_0)\geq 0\),则称 \(f\) 是半正定二次型,对应的实对称矩阵 \(\mathbf{A}\) 为半正定矩阵;
\(f(\mathbf{x}_0)\leq 0\),则称 \(f\) 是半负定二次型,对应的实对称矩阵 \(\mathbf{A}\) 为半负定矩阵;
\(f(\mathbf{x}_0)\) 可正可负,则称 \(f\) 是不定型二次型,对应的实对称矩阵 \(\mathbf{A}\) 为不定型矩阵。
由此可知,对称矩阵 \(\mathbf{A}\) 为正定矩阵的充要条件是特征值全为正。
除了使用特征值判断正定型,还有一个充要条件是是计算顺序主子式均为正,即 \[ a_{11}>0,\begin{vmatrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{vmatrix}>0,\cdots,\begin{vmatrix} a_{11}&\cdots&a_{1n}\\ \vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{n2} \end{vmatrix}>0 \] 这个定理也称作是霍尔维茨定理。
而判断负定型的充要条件是 \[ a_{11}<0,\begin{vmatrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{vmatrix}>0,\cdots,(-1)^k\begin{vmatrix} a_{11}&\cdots&a_{1n}\\ \vdots&\ddots&\vdots\\ a_{21}&\cdots&a_{22} \end{vmatrix}>0 \] 即奇数阶主子式为负,偶数阶主子式为正。
其他情况为不定型。
多元凸函数
了解正定矩阵的判定,是为了引出以下定理:
如果 \(f(x_1,\cdots,x_n):C\subset R^n\to R^1\) 为二次可微多元函数,\(C\) 为凸集。那么 \(f\) 在 \(C\) 上为凸函数的充要条件是海森(hessian)矩阵 \(D^2(f)\) 在 \(C\) 上处处半正定。
例如 \(f(x_1,x_2)=10-2(x_2-x_1^2)^2,C=\{(x_1,x_2)|-11\leq x_1\leq 1,-1\leq x_2\leq 1\}\),我们计算其海森矩阵 \[ D^2(f)=\begin{bmatrix} 8(x_2-3x_1^2)&8x_1\\ 8x_1&-4 \end{bmatrix} \] 可知由于其在 \((0,1)\) 处结果为 \(\begin{bmatrix} 8&0\\ 0&-4 \end{bmatrix}\),是不定矩阵,因此 \(f\) 在 \(C\) 上并非处处半正定,故其不是凸函数。
无约束最优化问题
回到最开始的引子,求解多元函数最优化问题 \[ \min f(\mathbf{x}),\mathbf{x}\in R^n \] 那么根据以上多元函数的性质和定理,我们可以知道,使得 \(D(f)=0\) 且 \(D^2(f)\) 为半正定时,称此点为极小值点。
换句话说,如果 \(f(\mathbf{x})\) 在 \(R^n\) 上是凸函数且一阶可微,那么其极小值点的充要条件为 \(D(f)=0\)。
无约束问题的算法框架
最优化问题中最常见的就是神经网络的参数学习问题,由于一个神经网络可能涉及到成千上万乃至百万级的参数,维度十分的高,每一次计算方程 \(\nabla f=0\) 显然是巨大的工作量,所以一般在计算机中使用迭代的方式去逼近(寻找)解。
从瞎子爬山到优化方法,我们可以总结出这样的算法框架:
给定初始点 \(x^{(0)}\in R^{n}\),精度 \(\epsilon>0\),令 \(k=0\)
若终止条件满足精度(例如 \(\|\nabla f(x^{(k)})\|\leq \epsilon\)),则终止算法,得解 \(x^{(k)}\);否则进行下一步
确定下降方向 \(d^{(k)}\) 使得 \[ \nabla f(x^{(k)})^T d^{k}<0 \]
确定步长 \(a_k>0\) 使得 \[ f(x^{(k)}+a_kd^{(k)})<f(x^{(k)}) \]
令 \(x^{(k+1)}=x^{(k)}+a_kd^{(k)},k=k+1\),回到第二步
在这样的算法框架中,我们需要确定如下几个细节:
- 下降方向
- 终止条件
- 步长的选取(线性搜索)
下降方向
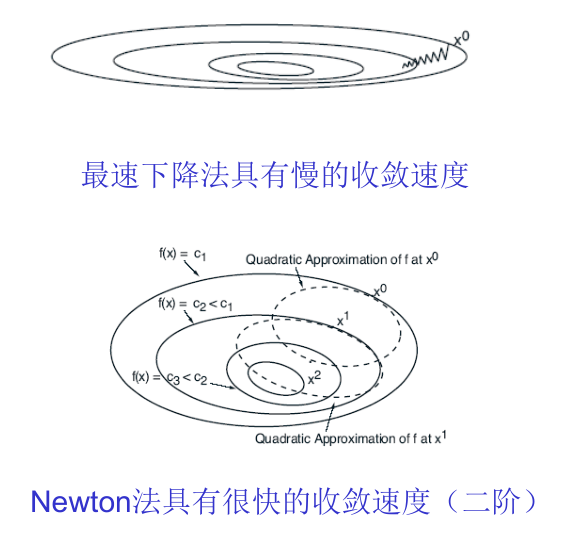
下降方向的确定有许多种算法思路,其中最常见的就是两种:最速下降法(梯度下降法)和牛顿法。
梯度下降法公式如下 \[
x^{k+1}=x^k-a^k\nabla f(x^k)
\] 牛顿法公式如下 \[
x^{k+1}=x^k-a^k(\nabla^2 f(x^k))^{-1}\nabla f(x^k)
\] 
收敛性与收敛速度
当一个算法只有当选定初始点后产生的点列才收敛于 \(x^*\),我们称该算法为局部收敛的算法;
当一个算法任意初始点产生的点列都收敛于 \(x^*\),我们称该算法为全局收敛的算法。
局部收敛是全局收敛的基础。
我们定义收敛速度的公式如下 \[ \lim_{k\to \infin}\frac{\|x_{k+1}-x^*\|}{\|x_k-x^*\|^p}=\theta \] 若 \(p=1\) 且 \(0<\theta<1\),则称该算法具有线性收敛速度(或线性收敛的);
若 \(p=1\) 且 \(\theta=0\),则称该算法具有超线性收敛速度(或超线性收敛的);
若 \(p=2\) 且 \(0<\theta<\infin\),则称该算法具有平方收敛速度(或平方收敛的);
一般地,若 \(p>2\) 且 \(0<\theta<\infin\),则称该算法具有 \(p\) 阶收敛速度(或 \(p\) 阶收敛的)。
终止准则
对于一种算法,应该有某种终止准则使得迭代算法结束。
常用的终止准则有:
