模式识别-参数估计笔记
模式识别
前言
先验概率是可以通过训练集和先验知识易求得的,但类条件概率密度是难求的,主要的问题有两个:
- 很多情况下,已有的训练样本数总是显得太少;
- 用于表示特征的向量 \(\boldsymbol{x}\) 的维数过大时,计算负担更大。
这时候我们一般会像上一章所说的那样,譬如让 \(p(\boldsymbol{x}|\omega_j)\sim N(\boldsymbol{\mu}|\Sigma)\),即假设我们求类条件概率密度转化为求正态分布的参数,这种方式称作参数化,即使得类条件概率密度仅依赖于某些参数(例如在这里是均值和协方差矩阵)。
也可以让类条件概率密度参数化为其他分布密度(例如泊松分布),但此时的问题就转化为——估计(计算)参数。
而估计(计算)这些参数,主要有两种方式——最大似然估计和贝叶斯参数估计。
最大似然估计
基本原理
假设我们有 \(c\) 个样本集,\(D_1,D_2,\cdots,D_c\),而任意一个样本集所得到的类条件概率密度 \(p(\boldsymbol{x}|\omega_j)\) 是互相独立的。在前言中,我们目前的问题是,知道 \(p(\boldsymbol{x}|\omega_j)\) 的形式,但未知其参数,最大似然估计中,将参数写作 \(\boldsymbol{\theta}\) 的形式,每个参数值记作 \(\theta_1,\theta_2,\cdots,\theta_p\)(参数向量的维度与特征向量的维度不统一),通常可以写作 \(p(\boldsymbol{x}|\omega_j,\boldsymbol{\theta_j})\),这表示对于某一类条件概率密度的参数向量函数。
例如已知 \(p(x|\omega_j)\sim N(\mu,\sigma^2)\),即一个一维特征类条件概率密度满足正态分布的形式,那么我们求解类条件概率密度问题就转化为求解正态分布的参数 \((\mu,\sigma^2)\)。
那么我们把参数向量写作 \(\boldsymbol{\theta}_j=(\mu,\sigma^2)^T\),即对于 \(\omega_j\) 的类条件概率密度的参数向量,写作 \(p(x|\omega_j,\boldsymbol{\theta_j})\),此时特征向量维度为 1,参数向量维度为 2。
为简化问题,设样本集 \(D\) 中有 \(n\) 个样本 \(\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_n\),把上式写作 \(p(D|\boldsymbol{\theta})\),仅研究对于某个样本集的参数向量的计算,满足 \[ p(D|\boldsymbol{\theta})=\prod^n_{k=1}p(\boldsymbol{x}_k|\boldsymbol{\theta}) \]
采用属性条件独立性假设,各个分布独立,其联合分布即各个分布的乘积。
由于 \(D\) 是已知的,故实际上 \(p(D|\boldsymbol{\theta})\) 是一个关于 \(\boldsymbol{\theta}\) 的似然函数。
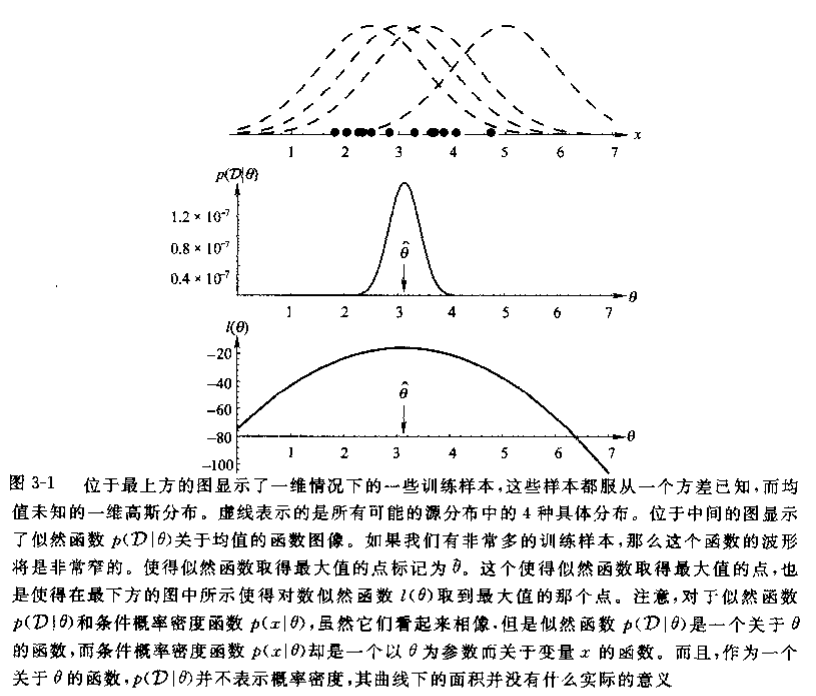
定义,梯度算子 \[ \nabla_{\boldsymbol{\theta}}=\left[\begin{array}{c} \frac{\partial}{\partial \theta_{1}} \\ \vdots \\ \frac{\partial}{\partial \theta_{p}} \end{array}\right] \] 定义对数似然函数 \[ \begin{align} l(\boldsymbol{\theta}) &=\ln{p(D|\boldsymbol{\theta})}\\ &=\sum^n_{k=1}\ln{p(\boldsymbol{x}_k|\boldsymbol{\theta})} \end{align} \]
这里主要是将乘积转化为求和,可以更好的运算。
那么,记 \[ \hat{\boldsymbol{\theta}}=\arg{\max_{\boldsymbol{\theta}}{l(\boldsymbol{\theta})}} \] 且 \[ \nabla_{\boldsymbol{\theta}}l=\sum^n_{k=1}\nabla_{\boldsymbol{\theta}}\sum^n_{k=1}\ln{p(\boldsymbol{x}_k|\boldsymbol{\theta})} \] 我们得到最大似然估计值 \(\boldsymbol{\theta}\) 的必然条件为 \[ \nabla_{\boldsymbol{\theta}}l=0 \]
根据此条件得到的 \(\hat{\boldsymbol{\theta}}\) 可能是局部极大值,或是拐点,需要讨论。类似于函数讨论最大值点。
理论上来说,如果训练样本个数越多,其中的样本就越具有代表性,参数值也就越接近真实值。
正态分布:\(\boldsymbol{\mu}\) 未知
根据上一篇文章,可以知道多维正态分布的对数似然函数为 \[ l(\boldsymbol{\mu})=-\frac{d}{2}\ln{2\pi}-\frac{1}{2}\ln{|\Sigma_i|}-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_i)^T\Sigma^{-1}_i(\boldsymbol{x}-\boldsymbol{\mu}_i) \]
在这里 \(\boldsymbol{\theta}=\boldsymbol{\mu}\)。
求得 \[ \nabla_\boldsymbol{\mu}l=\Sigma^{-1}(\boldsymbol{x}_k-\boldsymbol{\mu}) \] 令 \[ \nabla_\boldsymbol{\mu}l=0 \] 求得 \[ \hat{\boldsymbol{\mu}}=\frac{1}{n}\sum^n_{k=1}\boldsymbol{x}_k \] 显然最大似然估计的结果满足我们直觉所得。
正态分布:\((\mu,\sigma^2)\) 未知
根据上一篇文章,可以知道一维正态分布的对数似然函数为 \[ l(\boldsymbol{\theta})=-\frac{1}{2}\ln{(2\pi\theta_2)}-\frac{1}{2\theta_2}(x_k-\theta_1) \]
在这里 \(\boldsymbol{\theta}=(\mu,\sigma^2)^T\)。
求梯度可得 \[ \boldsymbol{\nabla}_{\theta} \mid=\boldsymbol{\nabla}_{\boldsymbol{\theta}} \ln p\left(x_{k} \mid \boldsymbol{\theta}\right)=\left[\begin{array}{c} \frac{1}{\theta_{2}}\left(x_{k}-\theta_{1}\right) \\ -\frac{1}{2 \theta_{2}}+\frac{\left(x_{k}-\theta_{1}\right)^{2}}{2 \theta_{2}^{2}} \end{array}\right] \] 易得 \[ \hat{\mu}=\frac{1}{n}\sum^n_{k=1}x_k\\ \hat{\sigma^2}=\frac{1}{n}\sum^n_{k=1}(x_k-\hat{\mu})^2 \] 对于多元正态分布,我们也可以求得满足直觉的结果。