分组加密模式攻击
ECB
加密流程
ECB
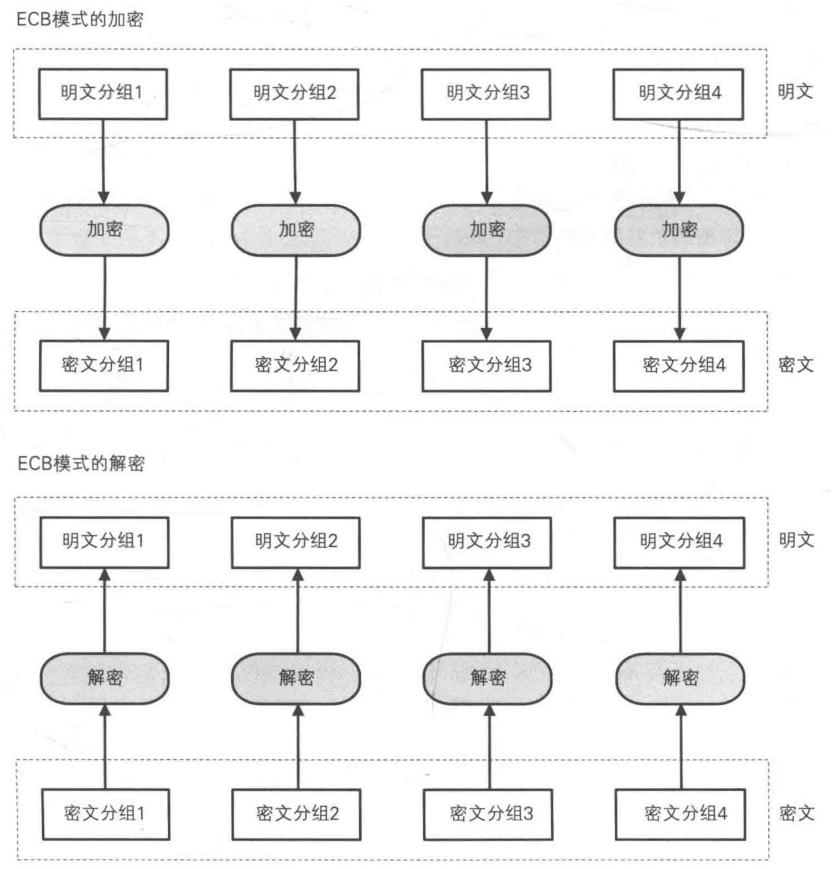
模式又称电子密码本模式,采用将明文分组后直接进行加密成为密文分组。
 ecb-mode
ecb-mode
特点:ECB
模式中,明文分组与密文分组是一一对应的关系。
改变密文顺序
由于明文分组和密文分组是一一对应的关系,如果我们将密文分组的顺序改变,对应的明文分组的顺序也会改变,也就是说攻击者无需
key 即可操纵明文。
尾字节爆破
由于 ECB
模式的特殊性,输入相同的明文可以得到相同的密文,当我们拥有加密机时,我们通过向未知字符串的明文中插入数据,枚举爆破尾字节的信息,本质上是一种选择明文攻击。
假设未知的明文是 XXXXXXXX,构造数据
0000000X XXXXXXX,其中 0000000
为我们已知的明文,放入加密机加密得到密文
01234567 76543210,其中 01234567 为明文块
0000000X 所对应的密文块。
我们爆破该明文块的最后一个字节,直到尝试发现 0000000Q
加密得到的密文块也是
01234567,那么就得到了明文的第一个字节为
Q。
以此类推,我们最终能通过选择明文的方式破解完整的明文。
假设存在加密机
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
class AESECBMachine:
def __init__(self, key: bytes):
self.key = key
self.machine = AES.new(key, AES.MODE_ECB)
def encrypt(self, msg: bytes):
return self.machine.encrypt(msg)
def decrypt(self, cipher: bytes):
return self.machine.decrypt(cipher)
machine = AESECBMachine(b'0123456789abcefg')
MESSAGE = b"Hope you can happy"
def get(msg: bytes):
return machine.encrypt(pad(msg + MESSAGE, 16))
|
其中通过 get
函数可以得到加密机加密的结果,MESSAGE
为我们需要破解的明文。
我们首先可以尝试自己填充明文,得到未知明文长度
1
2
3
4
5
6
7
8
9
10
| def test_length(block_size: int):
last_cipher = get(b"")
for pad_size in range(1, block_size):
cipher = get(bytes(pad_size))
if len(last_cipher) != len(cipher):
return len(last_cipher) - pad_size
block_size = 16
message_length = test_length(block_size)
print("message length:", message_length)
|
随后我们进行尾字节爆破:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| import string
known_message = b""
message_table: str = string.printable
for block_count in range(message_length // block_size + 1):
unknown_length = block_size
for times in range(block_size):
test = bytes(unknown_length - 1)
check_result = get(test)[:block_count * block_size + unknown_length]
for test_bytes in message_table:
result = get(test + known_message + test_bytes.encode())[:block_count * block_size + unknown_length]
if result == check_result:
known_message += test_bytes.encode()
print("Crack Message:", known_message)
break
unknown_length -= 1
|
CBC
加密流程
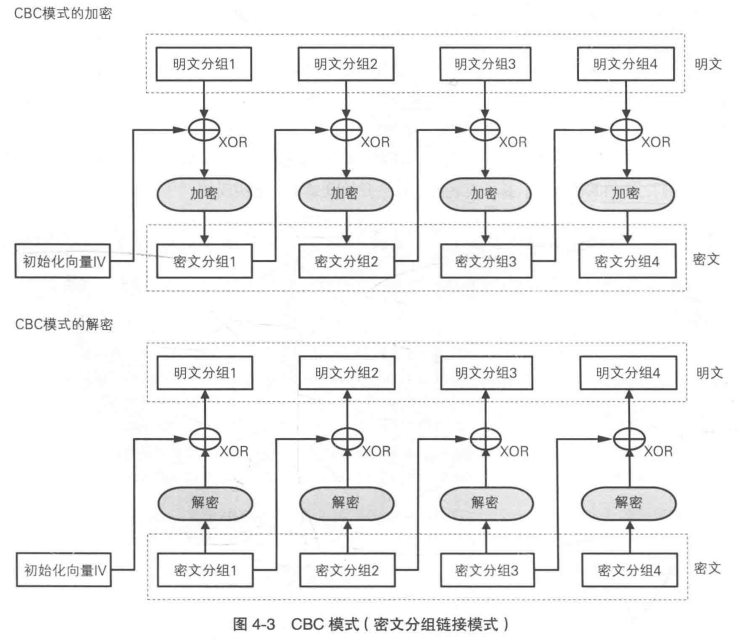
CBC
模式,即密文分组链接模式,特点是需要一个噪声(nonce),每次都与明文异或后再加密。
 cbc-mode
cbc-mode
选择密文
假设有这么一个 AES 预言机,
1
2
3
4
5
6
7
8
9
10
11
12
13
| from Crypto.Cipher import AES
class AESCBCOracle:
key = b"0123456789abcdef"
iv = b"qsdzyydsqsdzyyds"
@classmethod
def encrypt(cls, pt: bytes) -> bytes:
return AES.new(cls.key, AES.MODE_CBC, cls.iv).encrypt(pt)
@classmethod
def decrypt(cls, ct: bytes) -> bytes:
return AES.new(cls.key, AES.MODE_CBC, cls.iv).decrypt(ct)
|
其中的 key 是预言机内部状态,从解密的角度来看
1
2
3
4
| pt1 = D(ct1) ^ iv
pt2 = D(ct2) ^ ct1
pt3 = D(ct3) ^ ct2
...
|
如果说此时可以选择密文,令
ct1=ct2=0,那么解密流程就会变为
1
2
| pt1 = D(0) ^ iv
pt2 = D(0) ^ 0
|
也就是说,此时明文块 1 和 明文块 2 构成关系
pt1^pt2=iv,这样便从中泄露出了初始化向量。
1
2
3
4
| from Crypto.Util.strxor import strxor
pt = AESCBCOracle.decrypt(bytes(32))
iv = strxor(pt[:16], pt[16:])
|
比特反转攻击
由于密文和明文之间的关系总是保持为
1
2
3
4
| pt1 = D(ct1) ^ iv
pt2 = D(ct2) ^ ct1
pt3 = D(ct3) ^ ct2
...
|
此时如果说我对密文 ct1
的一个位进行了改变,那么相同的,pt2
的一个位也会进行改变。
这对初始化向量 iv 来说也是一样的。
一般来说,只要我们能够控制初始化向量 iv,那么明文
pt1
就受到了我们的控制,这对于其他密文块而言也是同理的。
CTR
加密流程
 ctr-mode
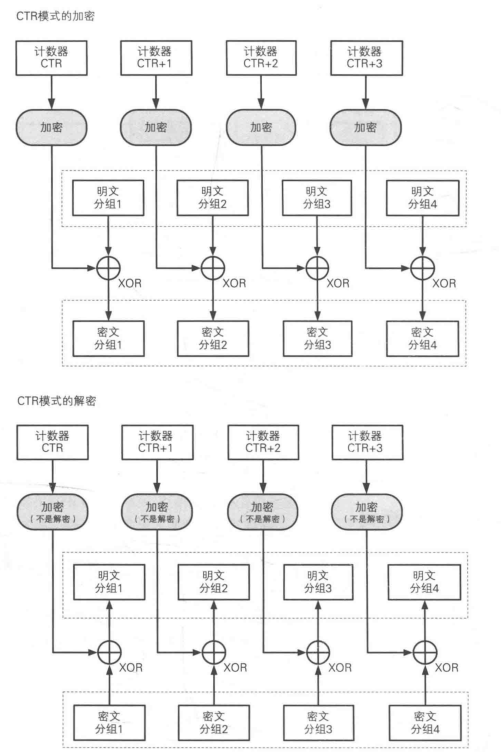
ctr-mode
特点:类似一次一密,每次加密明文与新的随机字节流进行异或,此时加密算法更像是随机数发生器。
选择明文
如果 CTR 中 Counter
的初始值恒定,那么我们每次投入的明文都会与同一组随机字节流异或,即 \[
m_1\oplus k=c_1\newline
m_2\oplus k=c_2
\] 考虑 \(m_1\)
是我们想要获得的消息,而 \(m_2\)
是我们可控的,那么就可以将两个密文异或得到 \[
c_1\oplus c_2=m_1\oplus m_2
\] 这样,我们再对其异或我们可控的 \(m_2\) 就得到了秘密消息。
多次一密
与选择明文类似,只是此时明文分段,得到 \[
m_1\oplus k=c_1\newline
m_2\oplus k=c_2\newline
\vdots\newline
m_l\oplus k=c_l
\] 此时退化成多次一密问题。
通用攻击方法
Padding Oracle(填充攻击)
通常情况下,明文的长度很可能不满足块加密算法所要求的固定块大小。因此,在进行块加密之前,需要采用一些方法对明文进行填充,以使其满足块加密算法的要求。
其中,最常见的填充算法是
PKCS#7(公钥密码学标准#7),其特点是填充内容的字节值等于需要填充的字节数。
如果要填充 4 个字节,那么填充的内容就会是
b'\x04\x04\x04\x04'。
PKCS#7
的好处是在解密时能够正确地识别和删除填充内容,从而还原出原始的明文数据。
但这也会使得 CBC 模式存在弱点,由于密文和明文之间的关系总是保持为
1
2
3
4
| pt1 = D(ct1) ^ iv
pt2 = D(ct2) ^ ct1
pt3 = D(ct3) ^ ct2
...
|
基于比特反转攻击和 PKCS#7
的特点,如果说解出的明文的最后一个字节不为填充字节,就会发生错误,那么可以通过控制
ct2 来控制 pt3,基于错误泄露明文。
我们没有解密机,只能通过服务端的返回判断解密是否发生了错误。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
class AESCBCOracle:
key = b"0123456789abcdef"
iv = b"qsdzyydsqsdzyyds"
@classmethod
def encrypt(cls, pt: bytes) -> bytes:
return AES.new(cls.key, AES.MODE_CBC, cls.iv).encrypt(pad(pt, len(cls.key)))
@classmethod
def try_decrypt(cls, ct: bytes) -> None:
unpad(AES.new(cls.key, AES.MODE_CBC, cls.iv).decrypt(ct), len(cls.key))
@classmethod
def known_ct(cls) -> bytes:
flag = b'flag{qsdz_yyds_dO_u_kn0w?Padd1ng_i5_vUln_in5tead!}'
ct = AESCBCOracle.encrypt(flag)
return ct
|
假设我们可以通过 known_ct 获取已知密文,通过
try_decrypt 判断解密是否成功。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| def try_once(ct: bytes) -> bool:
"""
尝试解密,如果错误返回False
Args:
ct (bytes): 尝试解密的密文
Returns:
bool: 是否发生错误
"""
try:
AESCBCOracle.try_decrypt(ct)
except:
return False
return True
def expose_block(ct_blocks: list[bytes], index: int, block_size: int = 16):
"""
尝试去Padding攻击一个块,需要实现try_once函数
Args:
ct_blocks (list[bytes]): 所有的密文块
index (int): 想要攻击的密文块索引,不能超过len(ct_blocks)-1
block_size (int, optional): 块大小. Defaults to 16.
Returns:
tuple[bytes, bytes]: 返回一个中间明文块和明文块
"""
ct_start = b''.join(ct_blocks[:index])
ct_end = ct_blocks[index+1]
chosen_ct = ct_blocks[index]
middle_ct = [0] * block_size
for i in range(block_size):
pad_byte = i + 1
idx = block_size - pad_byte
fake_ct = [c ^ pad_byte for c in middle_ct]
for try_byte in range(256):
fake_ct[idx] = try_byte
if try_once(ct_start + bytes(fake_ct) + ct_end):
middle_ct[idx] = try_byte ^ pad_byte
break
expose_pt = [c ^ m for c, m in zip(chosen_ct, middle_ct)]
return bytes(middle_ct), bytes(expose_pt)
ct = AESCBCOracle.known_ct()
print(f'{ct = }')
block_size = 16
ct_blocks = [ct[i:i+block_size] for i in range(0, len(ct), block_size)]
for i in reversed(range(len(ct_blocks) - 1)):
middle_ct, expose_ct = expose_block(ct_blocks, i, block_size=block_size)
print(f'{expose_ct = }')
|
与 SQL 注入中的基于布尔的盲注类似。
重用密钥和初始化向量
重用密钥和初始化向量会使得攻击者可以利用选择密文攻击或选择明文攻击,通过差异化计算出相关信息,一般建议在实际程序中随机化密钥和随机化初始化向量。


