模式识别-贝叶斯决策论笔记

发表于 2023-02-26 更新于 2023-04-20 本文字数： 22k 阅读时长 ≈ 20 分钟

有关贝叶斯决策论的简要笔记

模式识别

贝叶斯决策论

公式

贝叶斯概率是由贝叶斯提出的一种“逆概”的概念，计算正向概率的方法对于当时的人们而言是十分轻易的，例如“假设容器中有N个白球，M个黑球，随机抽取一个球，抽取的是白球的概率是多少”。但一个自然而然的问题是与正向概率相反的，例如“随机抽取一个（多个）球，知道了抽取的概率，那么容器内黑白球的比例是多少”。

这个问题是现实的，因为往往人们对一个事件进行评价的时候，无法掌握因，而只能知晓果，由果推因是人们常做的事情。

条件概率

要理解贝叶斯公式首先需要了解条件概率，定义 \(P(A|B)\) 为在事件 \(B\) 发生后，事件 \(A\) 发生的概率。

条件概率公式： \[ P(A|B)=\frac{P(AB)}{P(B)} \] 其中 \(P(A|B)\) 是条件概率，\(P(AB)\) 是两个事件共同发生的概率，\(P(B)\) 是事件 \(B\) 作为独立事件单独发生的概率。

例如掷骰子，掷出3点以上的概率为 \(P(\text{掷出3点以上})=1/2\)，而掷出3点以上又为偶数的概率为 \(P(\text{掷出3点以上又为偶数})=1/3\)，那么我们可以计算得到已经掷出3点以上后，点数为偶数的概率为 \[ P(\text{掷出3点以上}|\text{点数为偶数})=\frac{P(\text{掷出3点以上又为偶数})}{P(\text{掷出3点以上})}=2/3 \] 显然，符合我们通过古典概型计算得到的结果。

概率密度函数

定义连续型随机变量的概率密度为 \[ F(x)=\int^\infty_{-\infty}f(t)\mathrm{d}t \] 其中 \(F(x)\) 为随机变量 \(X\) 的分布函数，则称 \(f(x)\) 为 \(X\) 的概率密度函数，简称概率密度或密度函数。

而分布函数的定义为 \[ F(\xi)=P(X<\xi) \] 反之有 \[ f(x)=\frac{\mathrm{d}F(x)}{\mathrm{d}x} \]

全概率公式

\[ P(B)=P(B|A)P(A)+P(B|\bar{A})P(\bar{A}) \]

用于求贝叶斯公式中的无条件概率 \(P(B)\)，其中事件 \(\bar{A}\) 代表事件 \(A\) 不发生。

完整公式有 \[ \begin{align*} P(B)&=P(BA_1)+P(BA_2)+\cdots+P(BA_n)\\ &=P(B|A_{1}) P(A_{1})+P(B|A_{2})P(A_{2})+\cdots+P(B|A_{n})P(A_{n})\\ &=\sum^n_{i=1}P(A_i)P(B|A_i) \end{align*} \]

贝叶斯公式

通过条件概率公式变形，可以得到 \[ P(AB)=P(A)P(B|A)=P(B)P(A|B) \] 整理可得贝叶斯公式 \[ P(A|B)=P(A)\frac{P(B|A)}{P(B)} \] 其中我们把 \(P(A)\) 称作先验概率，即事件 \(A\) 发生的概率，称为先验是因为该概率并不考虑事件 \(B\) 的影响，即在事件 \(B\) 发生前，对事件 \(A\) 概率的一个评估。

\(P(A|B)\) 称作后验概率，即事件 \(B\) 发生后，事件 \(A\) 发生的概率，也是对事件 \(A\) 概率的重新评估。

而因子 \(P(B|A)/P(B)\) 称作可能性函数（likelihood），也是一个调整因子，使得预估概率更加接近真实概率。（\(P(B)\) 也称作证据概率（evidence probability））

\(P(B)\) 可用全概率公式求解。

故贝叶斯公式可以表达为：**后验概率=先验概率*可能性函数**

根据可能性函数的公式，我们可以知道：

当“可能性函数>1”时，先验概率被增强，事件 \(A\) 发生的概率增大；

当“可能性函数=1”时，意味着事件 \(B\) 无助于判断事件 \(A\) 发生的概率；

当“可能性函数<1”时，先验概率被削弱，事件 \(A\) 发生的概率减小。

贝叶斯公式的意义在于帮助我们在有限信息的情况下，尽量得到客观概率的近似值（先验概率由我们主观估计，通过可能性函数进行修正我们的先验概率得到后验概率，即客观概率的近似值）。

实际应用

已知两个一模一样的容器，容器 \(A_1\) 中有 30 个白球和 10 个黑球，而容器 \(A_2\) 中有 20 个白球和 20 个黑球，现在从中随机摸出一个球是白球，请问这个白球来自一号容器的概率是多少？

我们可以列出下面一个表：

容器/分类	\(A_1\)	\(A_2\)
白球	30	20
黑球	10	20

可以知道先验概率 \(P(A_1)=P(A_2)=0.5\)（不受摸出来的球的影响下，球来自哪个容器的概率）

假定事件 \(B\) 为摸出白球，有 \(P(B)=(30+20)/80=5/8\)

而已知在容器 \(A_1\) 中摸出白球的概率为 \(P(B|A_1)=30/40=3/4\)

那么我们要求的后验概率 \(P(A_1|B)=P(A_1)P(B|A_1)/P(B)=3/5\)，即在抽取的球为白球时，球来自容器 \(A_1\) 的概率为 0.6。

其中可能性函数 \(P(B|A_1)/P(B)=1.2\)，即先验概率被增强了。

举个更具体的例子，因为艾滋病潜伏期很长，所以即便感染了也可能在很长的一段时间，身体没有任何感觉，所以艾滋病检测的假阳性会导致被测人非常大的心理压力。

你可能会觉得，检测准确率都99%了，误测几乎可以忽略不计了吧？所以你觉得这人肯定没有患艾滋病了对不对？

让我们用贝叶斯定理算一下，就会发现你的直觉是错误的。

假设某种疾病的发病率是0.001，即1000人中会有1个人得病。现在有一种试剂可以检验患者是否得病，它的准确率是0.99，即在患者确实得病的情况下，它有99%的可能呈现阳性。它的误报率是5%，即在患者没有得病的情况下，它有5%的可能呈现阳性。

现在有一个病人的检验结果为阳性，请问他确实得病的可能性有多大？

病人的检验结果为阳性（新的信息）记为事件 \(B\)，他得病记为事件 \(A\)。

那么要求的问题就是 \(P(A|B)\)，也就是病人的检验结果为阳性 \(P(B)\)，他确实得病的概率 \(P(A)\)。

已知信息为这种疾病的发病率是 0.001，即 \(P(A)=0.001\)

试剂可以检验患者是否得病，准确率是 0.99，也就是在患者确实得病的情况下\(P(A)\)，它有 99% 的可能呈现阳性 \(P(B)\)，所以 \(P(B|A)=0.99\)

试剂的误报率是 5%，即在患者没有得病的情况下，它有 5% 的可能呈现阳性。得病我们记为事件 \(A\)，那么没有得病就是事件 \(A\) 的反面，记为 \(\bar{A}\)，所以这句话就可以表示为 \(P(B|\bar{A})=0.05\)

可能性函数为 \(P(B|A)/P(B)=19.4346\)，可以知道先验概率被增强，得到后验概率为 \(P(A|B)=0.0194\)，即筛查的准确率都到了 99% 了，通过体检结果有病（阳性）确实得病的概率也只有 1.94%。

由于发艾滋病实在是小概率事件，所以当我们对一大群人做艾滋病筛查时，虽说准确率有 99%，但仍然会有相当一部分人因为误测而被诊断为艾滋病，这一部分人在人群中的数目甚至比真正艾滋病患者的数目还要高。

造成这么不靠谱的误诊的原因，是无差别地给一大群人做筛查，而不论测量准确率有多高，因为正常人的数目远大于实际的患者，所以误测造成的干扰就非常大了。

根据贝叶斯定理，我们知道提高先验概率，可以有效的提高后验概率。

所以解决的办法倒也很简单，就是先锁定可疑的人群，比如10000人中检查出现问题的那10个人，再独立重复检测一次。因为正常人连续两次体检都出现误测的概率极低，这时筛选出真正患者的准确率就很高了，这也是为什么许多疾病的检测，往往还要送交独立机构多次检查的原因。

这也是为什么艾滋病检测第一次呈阳性的人，还需要做第二次检测，第二次依然是阳性的还需要送交国家实验室做第三次检测。

决策论

定义

我们首先定义 \(\boldsymbol{x}\) 为特征向量，假定 \(\boldsymbol{x}\) 是一个连续随机变量，其分布取决于类别状态，表示为 \(p(\boldsymbol{x}|\omega)\)，将该概率密度函数称作类条件概率密度（class-conditional probability），即类别状态为 \(\omega\) 时 \(\boldsymbol{x}\) 的概率密度函数，又叫做似然（likelihood）。通俗理解为分类作为概率密度函数的条件。

其中 \(p(\boldsymbol{x})\) 为证据概率（evidence probability），\(P(\omega_i|\boldsymbol{x})\) 为后验概率（posterior probability），而 \(P(\omega_i)\) 为先验概率（prior probability）。

贝叶斯分类

对一个模式（pattern）进行分类，只根据先验概率进行决策是不现实的，这会导致分类永远只有一个结果。

例如取 \(\omega_1,\omega_2\) 为鲈鱼和鲑鱼，可知鲑鱼要比鲈鱼稀有，仅从客观概率上来说，\(P(\omega_1)>P(\omega_2)\)，此时无论如何判决都会选取 \(\omega_1\) 而非 \(\omega_2\)。

为了更好的分类，我们需要引入模式的特征（feature），结合特征进行分类。

而贝叶斯分类就是结合特征和贝叶斯概率的结果进行决策。

根据贝叶斯公式： \[ P(\omega_j|\boldsymbol{x})=\frac{p(\boldsymbol{x}|\omega_j)P(\omega_j)}{p(\boldsymbol{x})} \] 我们可以通过观测 \(\boldsymbol{x}\) 的值将先验概率 \(P(\omega_j)\) 转化为后验概率，即假设特征向量已知的条件下，类别为 \(\omega_j\) 的概率。

其中 \(p(\boldsymbol{x})\) 和 \(p(\boldsymbol{x}|\omega_j)\) 是可以通过已知的部分信息学习得知的。

例如取特征向量 \(\boldsymbol{x}\) 为鱼的长度，我们可以通过样本（sample）计算其长度总的出现频率（证据概率密度，或者也可以使用全概率公式求解）和在类别为 \(\omega_1,\omega_2\) 时长度的出现频率（类条件概率密度）。

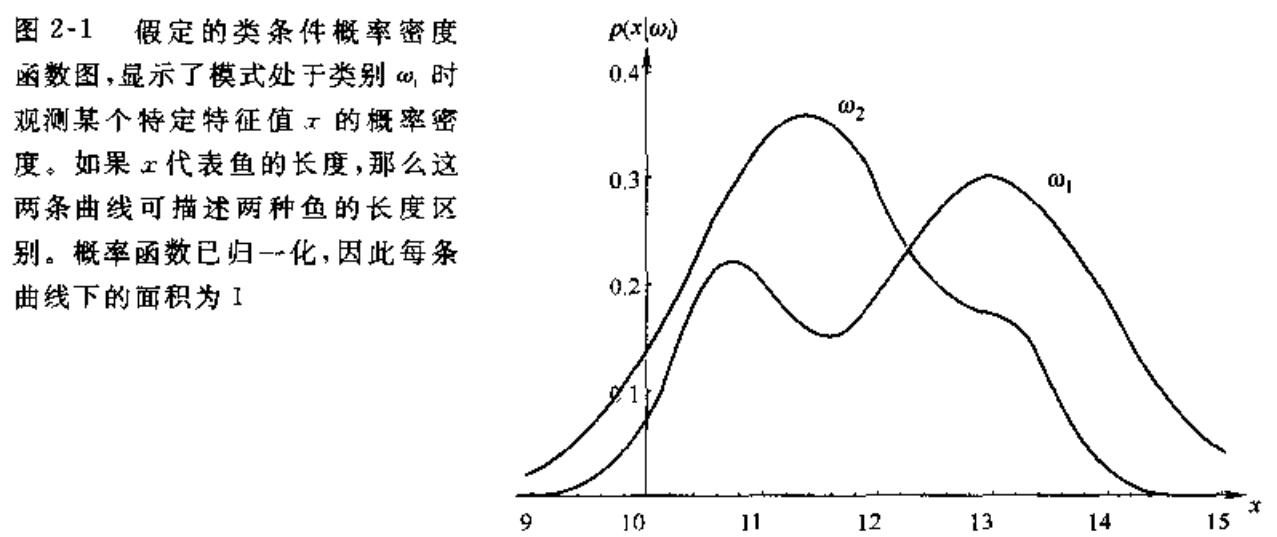
此时我们的判决规则为：

如果 \[ P(\omega_1|\boldsymbol{x})>P(\omega_2|\boldsymbol{x}) \] 则判决为 \(\omega_1\)。

正如贝叶斯概率的核心思想，我们通过先验概率（主观判断或客观事实）和已知信息（果或者似然）计算得到了后验概率（因或逆概）。

需要分清的是，\(p(\boldsymbol{x}|\omega_j)\) 是训练/学习（training/learning）计算得到的，而 \(P(\omega_j|\boldsymbol{x})\) 是用来预测（predict）的，在模式识别中是两个阶段。

连续特征下的决策论

将以上想法进一步正式化，推广为如下 4 种形式：

允许使用多于一个的特征
允许多余两种类别状态的情形
允许有其他行为而不仅仅是判定类别

其中，我们定义：

特征使用特征向量 \(\boldsymbol{x}\) 来描述多个特征
集合 \(\Omega=\{\omega_1,\omega_2\,\cdots,\omega_c\}\) 为有限的 \(c\) 个类别（state）集合
集合 \(A=\{\alpha_1,\alpha_2,\cdots,\alpha_a\}\) 为有限的 \(a\) 个可能的行动（action）集合

我们已知 \[ P(\omega_j|\boldsymbol{x})=\frac{p(\boldsymbol{x}|\omega_j)P(\omega_j)}{p(\boldsymbol{x})} \] 此时证据因子 \(p(\boldsymbol{x})\) 为 \[ p(\boldsymbol{x})=\sum^c_{j=1}p(\boldsymbol{x}|\omega_j)P(\omega_j) \] 对于简单化判决而言，判决规则是一个函数 \(\alpha(\boldsymbol{x})\)，值域为集合 \(\Omega\)。

最小误差概率决策

对于二分类问题，如果有某个观测值使得 \(P(\omega_1|\boldsymbol{x})>P(\omega_2|\boldsymbol{x})\)，那么我们自然的可以判断该模式来自于分类 \(\omega_1\)。

例如说，当先验概率 \(P(\omega_1)=2/3,P(\omega_2)=1/3\)，则后验概率 \(P(\omega_1 | \boldsymbol{x})\) 和 \(P(\omega_2|\boldsymbol{x})\) 如图所示

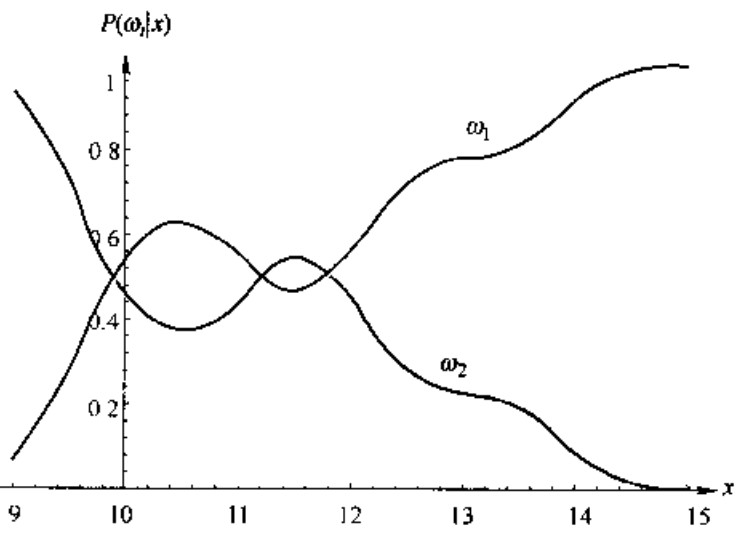
此时假定一个模式具有特征值 \(x=14\)，那么它属于 \(\omega_2\) 类的概率约为 0.08，属于 \(\omega_1\) 类的概率约为 0.92，在此次后验概率之和为 1.0，此时为最小化误差概率，故选择此模式属于 \(\omega_1\)。

同时该决策下的误差概率为： \[ P(error|\boldsymbol{x})=1-P(\omega_1|\boldsymbol{x}) \] 即有： \[ P(error|\boldsymbol{x})=\begin{cases} P(\omega_1|\boldsymbol{x})\text{,choose }\omega_2\\ P(\omega_2|\boldsymbol{x})\text{,choose }\omega_1 \end{cases} \] 可以验证，这种规则将平均误差概率最小化。

平均误差概率表示为 \[ P(error)=\int_{-\infty}^{\infty} P(error,x)\mathrm{d} x=\int_{-\infty}^{\infty} P(error|x) p(x)\mathrm{d}x \]

上述决策等价于，

若 \(P(\boldsymbol{x}|\omega_1)P(\omega_1)>P(\boldsymbol{x}|\omega_2)P(\omega_2)\)，则决策为 \(\boldsymbol{x}\in\omega_1\)；

若 \(P(\boldsymbol{x}|\omega_1)P(\omega_1)<P(\boldsymbol{x}|\omega_2)P(\omega_2)\)，则决策为 \(\boldsymbol{x}\in\omega_2\)。

即 \[ \frac{P(\boldsymbol{x}|\omega_1)}{P(\boldsymbol{x}|\omega_2)}>\frac{P(\omega_2)}{P(\omega_1)} \] 判决为 \(\omega_1\)。

其中， \[ \frac{P(\boldsymbol{x}|\omega_1)}{P(\boldsymbol{x}|\omega_2)} \] 称作似然比。

实例如下

某地区细胞识别中正常（\(\omega_1\)）和异常（\(\omega_2\)）两类的先验概率为 \(P(\omega_1)=0.9,P(\omega_2)=0.1\)，且知道两类的类概率密度函数 \(p(x|\omega_1),p(x|\omega_2)\)。

先有一细胞特征值为 \(x\)，查询类概率密度函数曲线有 \(P(x|\omega_1)=0.2,P(x|\omega_1)=0.4\)。

采用最小误差概率决策，得到 \[ P(x|\omega_1)/P(x|\omega_2)=1/2\\ P(\omega_2)/P(\omega_1)=1/9 \] 显然似然比大于先验概率反比，故判决为 \(x\in \omega_1\)，为正常细胞。

最小风险（损失）决策

基于最小误差概率的贝叶斯决策，仅考虑了最小化错误概率，未考虑决策所带来的损失，这是与实际应用不相符的，例如灭火系统、乙肝诊断等，总会存在一定的误判损失。

所以我们需要引入一个更一般的风险函数（loss function）来替代误差概率。

定义风险函数 \(\lambda(\alpha_i|\omega_j)\) 描述类别状态为 \(\omega_j\) 时，采取行动 \(\alpha_i\) 的风险（对风险的一个评估）。

或称为损失函数。

定义总风险 \(R\) 是与某一给定的判决规则相关的预期损失，且 \(R(\alpha_i|\boldsymbol{x})\) 是和行动 \(\alpha_i\) 相关的条件风险，总风险则表示为 \[ R=\int R(\alpha(\boldsymbol{x})|\boldsymbol{x})p(\boldsymbol{x})\mathrm{d}\boldsymbol{x} \]

\(\mathrm{d}\boldsymbol{x}\) 说明积分是在整个特征空间进行的。

可知，如果使得 \(R(\alpha_i|\boldsymbol{x})\) 对每个 \(\boldsymbol{x}\) 尽可能小，那么总风险 \(R\) 将被最小化。

故为了最小化总风险，对行动集合 \(A\) 计算条件风险 \[ R(\alpha_i|\boldsymbol{x})=\sum^c_{j=1}\lambda(\alpha_i|\omega_j)P(\omega_j|\boldsymbol{x}) \] 并选择行动 \(\alpha_i\) 使得 \(R(\alpha_i|\boldsymbol{x})\) 最小化。

最小化后的总风险值称为贝叶斯风险，记作 \(R^*\)。

对于二分类问题，可以将条件风险简化为 \[ R(\alpha_1|\boldsymbol{x})=\lambda_{11}P(\omega_1|\boldsymbol{x})+\lambda_{12}P(\omega_2|\boldsymbol{x})\\ R(\alpha_2|\boldsymbol{x})=\lambda_{21}P(\omega_1|\boldsymbol{x})+\lambda_{22}P(\omega_2|\boldsymbol{x}) \]

\(\lambda_{ij}\) 为简记 \(\lambda(\alpha_i|\omega_j)\)

判别的基本规则为当 \(R(\alpha_1|\boldsymbol{x})<R(\alpha_2|\boldsymbol{x})\) 时，则判为 \(\omega_1\)（描述为当决策为 \(\omega_1\) 的损失小于决策为 \(\omega_2\) 的损失时，判别为 \(\omega_1\)）。

化简为用后验概率的形式描述该公式：

如果 \[ (\lambda_{21}-\lambda_{11})P(\omega_1|\boldsymbol{x})>(\lambda_{12}-\lambda_{22})P(\omega_2|\boldsymbol{x}) \] 则判决为 \(\omega_1\)。

利用贝叶斯公式，改为用先验概率描述规则，则变更为：

如果 \[ (\lambda_{21}-\lambda_{11})p(\boldsymbol{x}|\omega_1)P(\omega_1)>(\lambda_{12}-\lambda_{22})p(\boldsymbol{x}|\omega_2)P(\omega_2) \] 则判决为 \(\omega_1\)。

另一种表示方式是，合理假设 \(\lambda_{21}>\lambda_{11}\) 的条件下：

如果 \[ \frac{p(\boldsymbol{x}|\omega_1)}{p(\boldsymbol{x}|\omega_2)}>\frac{\lambda_{12}-\lambda_{22}}{\lambda_{21}-\lambda_{11}}\frac{P(\omega_2)}{P(\omega_1)} \] 则判决为 \(\omega_1\)。

左式即为似然比。

这种判决规则的优势是，只依赖于 \(\boldsymbol{x}\) 的概率密度。

作出似然比函数，可以得知该种决策的判别边界与右式相关，当似然比大于判别边界时，判决为 \(\omega_1\)。

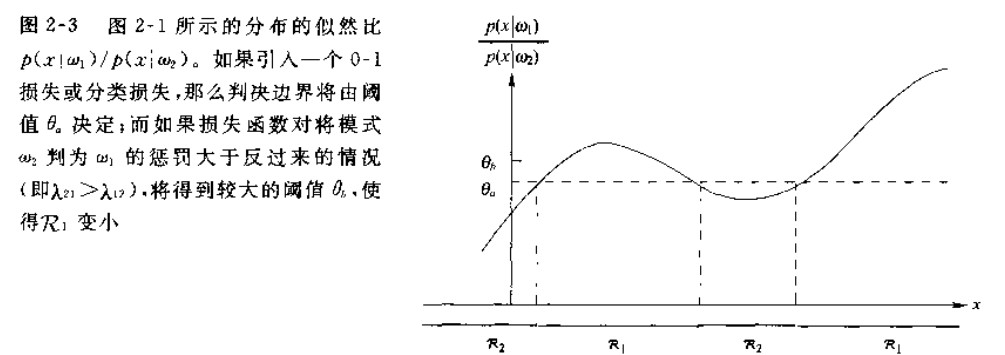
为方便判决，如上图，会选取一个阈值 \(\theta_m\) 使得 \[ \frac{p(\boldsymbol{x}|\omega_1)}{p(\boldsymbol{x}|\omega_2)}>\frac{\lambda_{12}-\lambda_{22}}{\lambda_{21}-\lambda_{11}}\frac{P(\omega_2)}{P(\omega_1)}>\theta_m \] 即为判决边界，如图虚线所示。

同时由公式可知，当 \(\lambda_{12}-\lambda_{22}=\lambda_{21}-\lambda_{11}\) 时，无论选择最小误差概率决策还是最小风险决策都是等价的。

实例如下

同最小误差概率决策中的实例，但此时给出损失表如下

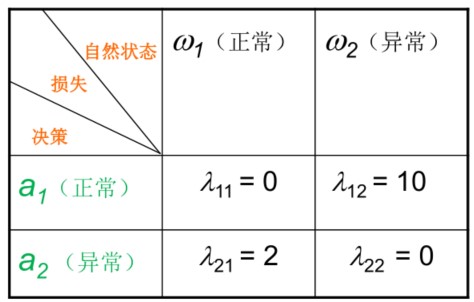
似然比为 0.5，计算损失比 \[ \frac{\lambda_{12}-\lambda_{22}}{\lambda_{21}-\lambda_{11}}=5 \] 显然 \[ \frac{1}{2}<5\times\frac{1}{9} \] 此时如果判决为 \(\omega_1\) 风险（损失）更大，故此时判决为 \(x\in \omega_2\)，为异常细胞。

最小误差率决策

如果要避免误判，自然要寻找一种判决规则使误判概率（即误差率）最小化。

这种情况下的损失函数就是所谓的“对称损失”或者“0-1 损失”函数： \[ \lambda(\alpha_i|\omega_j)=\begin{cases} 0,i=j\\ 1,i\neq j \end{cases} \] 其中要求 \(1<i,j<c\)。

从此简化模型可知，所有误判都是等代价的。

这个损失函数对应的条件风险就是平均误差概率，它的条件风险为： \[ \begin{align} R(\alpha_i|\boldsymbol{x})&=\sum^c_{j=1}\lambda(\alpha_i|\omega_j)P(\omega_j|\boldsymbol{x})\\ &=\sum_{i\neq j}P(\omega_j|\boldsymbol{x})\\ &=1-P(\omega_i|\boldsymbol{x}) \end{align} \] 其中 \(P(\omega_i|\boldsymbol{x})\) 是行为 \(\alpha_i\) 分类正确的条件概率。

这种情况下我们想最小化平均误差概率只要选取 \(i\) 使得后验概率 \(P(\omega_i|\boldsymbol{x})\) 最大即可。

或者说是最大化后验概率。

即有决策规则，对于任意 \(j\neq i\)，满足 \[ P(\omega_1|\boldsymbol{x})>P(\omega_j|\boldsymbol{x}) \] 则判决为 \(\omega_1\)。

实际应用

某人前往中高风险地区为特征 \(x\)，有表

分类	\(\alpha_1=\text{主动上报，自我隔离}\)	\(\alpha_2=\text{做核酸检测}\)	\(\alpha_1=\text{不上报，不做为}\)
\(\omega_1=\text{感染新冠}\)	5	50	10000
\(\omega_2=\text{未感染新冠}\)	60	3	0

知道 \(P(\omega_1|x)=0.01\)，\(P(\omega_2|x)=0.99\)

可以计算 \[ \begin{align} R(\alpha_1|x)&=\sum^2_{j=1}\lambda_{1j}P(\omega_j|x)\\ &=\lambda_{11}P(\omega_1|x)+\lambda_{12}P(\omega_2|x)\\ &=5\times0.01+60\times0.99\\ &=59.45\\ R(\alpha_2|x)&=3.47\\ R(\alpha_3|x)&=100\\ \end{align} \] 故可以得知，前往高风险地区时应采取的决策是做核酸（因为做核酸所导致的损失最低）。

分类器、判别函数与判别区域

判别函数

用后验概率与风险函数决策的方式，被称为模式分类器，有很多种方式来表示模式分类器，其中用的最多的是使用判别函数 \(g(\boldsymbol{x})\)。

使用单增函数嵌套的判决结果不变，即 \(f(g(\boldsymbol{x}))\) 对判决无影响，其中 \(f(\boldsymbol{x})\) 为单增函数

如果对于定 \(i\) 有任意的 \(j\) 满足 \[ g_i(\boldsymbol{x})>g_j(\boldsymbol{x}) \] 那么判决为 \(\omega_i\)。

此分类器可视为一个计算 \(c\) 个判别函数并选取最大判别值对应的类型的网络。

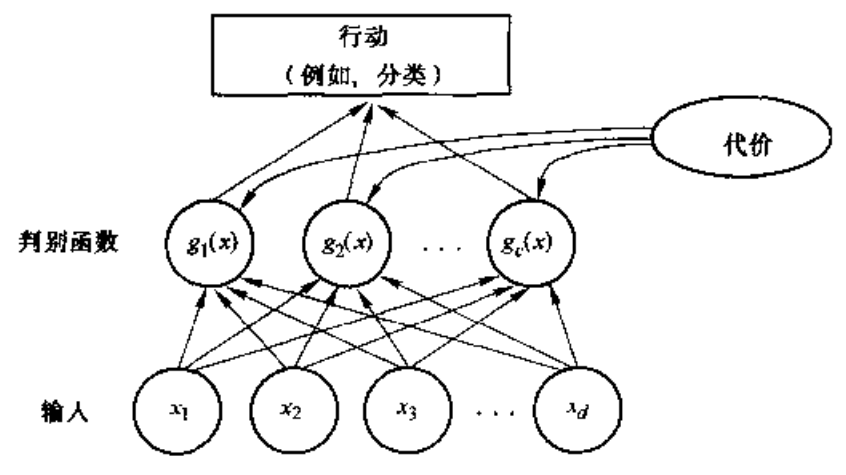
简单的判别函数可以表示为后验概率或者条件风险的负值，这样能让判别函数与最小的条件风险对应，判别函数的选择不是唯一的。

以下是常用的最小误差概率决策判别函数： \[ g_i(x)=P(\omega_i|\boldsymbol{x})\\ g_i(x)=p(\boldsymbol{x}|\omega_i)P(\omega_i)\\ g_i(x)=\ln p(\boldsymbol{x}|\omega_i)+\ln P(\omega_i) \] 还有最小风险决策判别函数： \[ g_i(x)=-R(\alpha_i|\boldsymbol{x}) \] 判决规则是相同的，每种判决规则均是将特征空间分成 \(c\) 个判决区域，\(R_1,R_2,\cdots,R_c\)。

如果对于所有的 \(j\neq i\) 有 \(g_i(\boldsymbol{x})>g_j(\boldsymbol{x})\)，那么 \(\boldsymbol{x}_i\) 属于 \(R_i\)。

此时该区域由判决边界来分割，其判决边界即判决空间中使判别函数值最大的曲面。

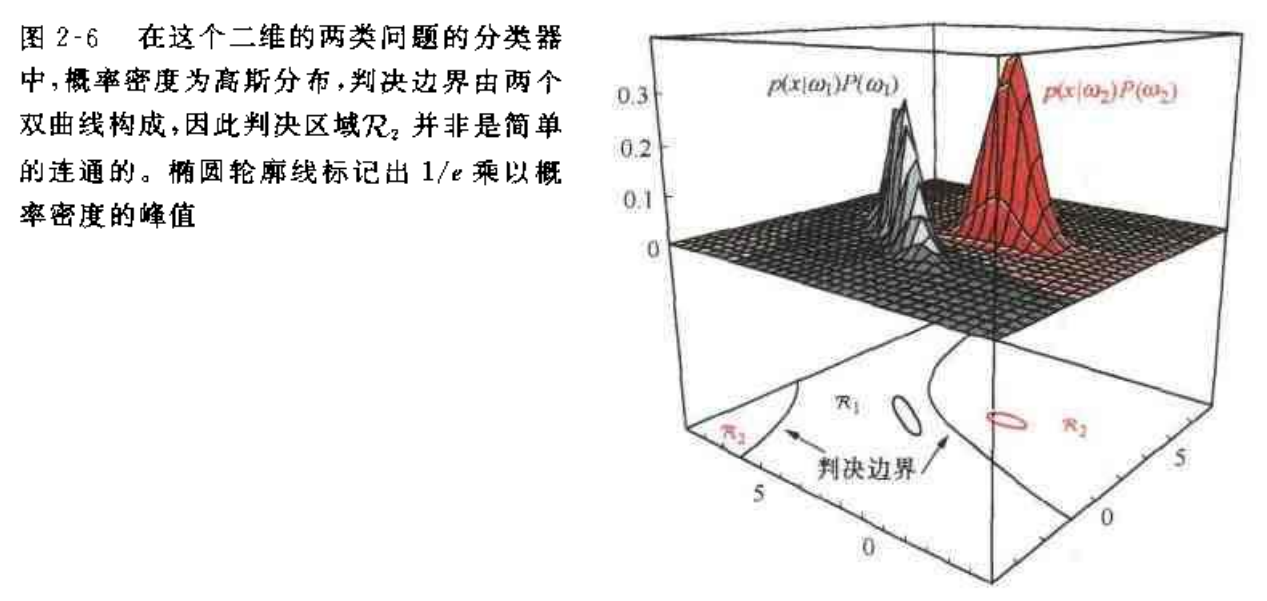
二类分类器

在该种情况下，使用判别函数 \[ g(\boldsymbol{x})=g_1(\boldsymbol{x})-g_2(\boldsymbol{x}) \] 判决规则为：

如果 \[ g(\boldsymbol{x})>0 \] 则判决为 \(\omega_1\)，否则判决为 \(\omega_2\)。

一般为简化会多使用以下形式： \[ g(\boldsymbol{x})=P(\omega_1|\boldsymbol{x})-P(\omega_2|\boldsymbol{x})\\ g(\boldsymbol{x})=\ln\frac{p(\boldsymbol{x}|\omega_1)}{p(\boldsymbol{x}|\omega_2)}+\ln\frac{P(\omega_1)}{P(\omega_2)} \]

朴素贝叶斯分类器

我们知道贝叶斯公式如下 \[ P(\omega|\boldsymbol{x})=\frac{P(\boldsymbol{x}|\omega)P(\omega)}{P(\boldsymbol{x})} \] 从中可以知道，估计后验概率 \(P(\omega_j|\boldsymbol{x})\) 的主要困难为：类条件概率 \(P(\boldsymbol{x}|\omega_j)\) 是所有属性上的联合概率，难以从有限的训练样本估计获得。

故采用“属性条件独立性假设”，即每个属性独立地对分类结果发生影响。

即 \(P(AB)=P(A)P(B)\)

基于属性条件独立性假设，可以将贝叶斯公式重写为 \[ P(\omega|\boldsymbol{x})=\frac{P(\boldsymbol{x}|\omega)P(\omega)}{P(\boldsymbol{x})}=\frac{P(\omega)}{P(\boldsymbol{x})}\prod^d_{i=1}P(x_i|\omega) \] 其中，\(d\) 为维度（属性数目），\(x_i\) 为 \(\boldsymbol{x}\) 在第 \(i\) 个维度（属性）上的取值。

其中条件风险函数为 \[ \begin{align} R(\alpha_i|\boldsymbol{x})&=\sum^c_{j=1}\lambda(\alpha_i|\omega_j)P(\omega_j|\boldsymbol{x})\\ &=\sum_{i\neq j}P(\omega_j|\boldsymbol{x})\\ &=1-P(\omega_i|\boldsymbol{x}) \end{align} \] 选择最小误差率决策，那么得到朴素贝叶斯分类的判别函数： \[ h(\boldsymbol{x})_{nb}=\arg\max_{\omega\in \Omega}{P(\omega)\prod^d_{i=1}P(x_i|\omega)} \] 即最大化后验概率。

朴素贝叶斯分类器的训练器的训练过程就是基于训练集 \(D\) 估计类先验概率 \(P(\omega)\) 并为每个属性估计条件概率 \(P(x_i|\omega)\)。

令 \(D_\omega\) 表示训练集 \(D\) 中 \(\omega\) 类样本组合的集合，若有重组的独立同分布样本，则可以容易估计出类先验概率： \[ P(\omega)=\frac{|D_\omega|}{D} \] 对离散属性而言，令 \(D_{\omega,x_i}\) 表示 \(D_\omega\) 中在第 \(i\) 个属性上取值为 \(x_i\) 的样本组成的集合，则条件概率 \(P(x_i|\omega)\) 可估计为 \[ P(x_i|\omega)=\frac{|D_{\omega,x_i}|}{|D_\omega|} \] 对于连续属性而言，可以考虑概率密度函数，假设 \(p(x_i|\omega)\sim N(\mu_{\omega,i},\sigma_{\omega,i}^2)\)，则 \[ P(x_i|\omega)=p(x_i|\omega) \] 此时 \(p(\boldsymbol{x}|\omega)\sim N(\boldsymbol{\mu}_\omega,\boldsymbol{\sigma}_\omega^2)\)，则参数的极大似然估计为 \[ \boldsymbol{\mu}_\omega=\frac{1}{|D_\omega|}\sum_{\boldsymbol{x}\in D_\omega}\boldsymbol{x}\\ \boldsymbol{\sigma}_\omega^2=\frac{1}{|D_\omega|}\sum_{\boldsymbol{x}\in D_\omega}(\boldsymbol{x}-\boldsymbol{\mu}_\omega)^2\\ \]

\((\boldsymbol{x}-\boldsymbol{\mu}_\omega)^2\) 表示向量积，即 \((\boldsymbol{x}-\boldsymbol{\mu}_\omega)(\boldsymbol{x}-\boldsymbol{\mu}_\omega)^T\)

正态分布下的贝叶斯分类

朴素贝叶斯分类过于简单，实际情况中无法满足属性条件独立性假设，往往属性之间具有相关性。

协方差

在统计学中，方差是用来度量单个随机变量的离散程度，而协方差一般用来刻画两个随机变量的相似程度（值越大越相似）。

方差的计算公式如下 \[ \sigma^2_x=\frac{1}{n}\sum^n_{i=1}(x_i-\bar{x})^2 \] 其中，\(n\) 表示样本量，\(\bar{x}\) 表示这一组随机数据的均值。

在此基础上，协方差的计算公式定义如下 \[ \sigma(x,y)=\frac{1}{n}\sum^n_{i=1}(x_i-\bar{x})(y_i-\bar{y}) \] 其中，\(\bar{x},\bar{y}\) 分别表示两个随机变量所对应的观测样本均值，由此可知，方差 \(\sigma_x^2\) 可视作随机变量 \(x\) 关于其自身的协方差 \(\sigma(x,x)\)。

给定 \(d\) 组随机变量（特征向量）\(\boldsymbol{x}_k,k=1,2,\cdots,d\)，则这些随机变量的方差为 \[ \sigma(\boldsymbol{x}_k,\boldsymbol{x}_k)=\frac{1}{n}\sum^n_{i=1}(x_{ki}-\bar{x}_k)^2,k=1,2,\cdots,d \] 其中 \(x_{ki}\) 代表特征向量的第 \(i\) 个维度的值，\(\bar{x}_k\) 代表该维度下的平均值。

而协方差为 \[ \sigma(\boldsymbol{x}_m,\boldsymbol{x}_k)=\frac{1}{n}\sum^n_{i=1}(x_{mi}-\bar{x}_m)(x_{ki}-\bar{x}_k),k=1,2,\cdots,d \] 因此，协方差矩阵定义为 \[ \Sigma=\left[\begin{array}{ccc} \sigma\left(x_{1}, x_{1}\right) & \cdots & \sigma\left(x_{1}, x_{d}\right) \\ \vdots & \ddots & \vdots \\ \sigma\left(x_{d}, x_{1}\right) & \cdots & \sigma\left(x_{d}, x_{d}\right) \end{array}\right] \in \mathbb{R}^{d \times d} \] 其中对角线上的元素为各随机变量的方差，非对角线上的元素为两两随机变量之间的协方差，且 \(\Sigma\) 为对称矩阵。

一维正态分布

对于一维正态分布，有密度函数 \[ p(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp{[{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}]} \] 其中均值 \[ \mu=E(x)=\int^{+\infty}_{-\infty}xp(x)\mathrm{d}x \] 方差 \[ \sigma^2=E[(x-\mu)^2]=\int^{+\infty}_{-\infty}(x-\mu)^2p(x)\mathrm{d}x \] 其中一维正态分布也可以简写为 \(p(x)\sim N(\mu,\sigma^2)\)。

一种分布的熵由下式给出 \[ H(p(x))=-\int p(x)\ln{p(x)}\mathrm{d}x \] 单位为奈特，如果对数换为 \(\log_2\)，则单位为比特。

可以证明正态分布在所有具有给定均值和方差的分布中具有最大熵。由中心极限定理所述，大量的小的、独立地随机分布的总和等效为正态分布。由于所有模式——鱼、手写字符、语音——都可以看成是由大量随机过程所组成的某个理想的模式或原型模式，所以实际上通常会选择正态分布作为实际的概率分布。

多维正态分布

设 \(d\) 维特征向量 \[ \boldsymbol{x}=(x_1,x_2,\cdots,x_d)^T \] 则 \(d\) 维正态分布定义为 \[ p(\boldsymbol{x})=\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}\exp[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})] \] 其中 \(\Sigma\) 是 \(d\) 维的协方差矩阵，\(|\Sigma|\) 代表行列式的值，\(\Sigma^{-1}\) 代表矩阵的逆，\((\boldsymbol{x}-\boldsymbol{\mu})^T\) 表示矩阵的转置（在这里是变为行向量）。

通常简写为 \[ p(\boldsymbol{x})=N(\boldsymbol{\mu},\boldsymbol{\Sigma}) \] 其中均值 \[ \boldsymbol{\mu}=E(\boldsymbol{x})=\int\boldsymbol{x}p(\boldsymbol{x})\mathrm{d}\boldsymbol{x} \] 协方差矩阵 \[ \Sigma=E[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^T]=\int (\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^Tp(\boldsymbol{x})\mathrm{d}\boldsymbol{x} \] 其中 \((\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^T\) 表示求向量内积。

其中某个向量的均值可以通过其属性的均值获得，即 \[ \begin{align} \mu_i&=E(x_i)\\ \sigma_{ij}^2&=E[(x_i-\mu_i)(x_j-\mu_j)]\\ &=\iint(x_i-\mu_i)(x_j-\mu_j)p(x_i,x_j)\mathrm{d}{x_i}\mathrm{d}{x_j} \end{align} \] 当 \(i=j\) 时（对角线元素），\(\sigma_{ij}\) 反映样本 \(x_i\) 在 \(d\) 维特征空间各方向的发散程度；

当 \(i\neq j\) 时，\(\sigma_{ij}\) 反映各特征间的统计相关性。

这里需要严格限定 \(\Sigma\) 是正定矩阵，使得其行列式为正值。

分类器

设各类样本的类概率密度均满足正态分布，即 \[ p(\boldsymbol{x}|\omega_i)\sim N(\boldsymbol{\mu},\boldsymbol{\Sigma}) \] 根据最小误差概率决策，判别函数为 \[ g_i(\boldsymbol{x})=p(\boldsymbol{x}|\omega_i)p(\omega_i)=\max_{1\leq j\leq c}{(p(\boldsymbol{x}|\omega_j),p(\omega_j))} \] 或者使用 \[ \begin{align} g_i(\boldsymbol{x})&=\ln{p(\boldsymbol{x}|\omega_i)}+\ln{p(\omega_i)}\\ &=-\frac{d}{2}\ln{2\pi}-\frac{1}{2}\ln{|\Sigma_i|}-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_i)^T\Sigma^{-1}_i(\boldsymbol{x}-\boldsymbol{\mu}_i)+\ln{P(\omega_i)} \end{align} \] 分以下三种情况讨论决策结果。

情况一：\(\Sigma=\sigma^2I\)

各类协方差矩阵相等，\(\Sigma_i=\Sigma_j=\Sigma\)
各特征统计独立，\(\sigma_{ij}^2=0,i\neq j\)
样本各方向的发散程度一致 \(\sigma_{ij}^2=\sigma^2,i=j\)

即 \[ \Sigma=\begin{bmatrix} \sigma^2 & 0 & \cdots & 0\\ 0 & \sigma^2 & \cdots & 0\\ \cdots & \cdots & \cdots & \cdots\\ 0 & 0 & \cdots & \sigma^2 \end{bmatrix} \] 此时 \(\Sigma=\sigma^2I\)，故 \(\Sigma^{-1}=\frac{1}{\sigma^2}I\)，其中 \(I\) 为单位矩阵。

故判别函数化简为 \[ \begin{align} g_i(\boldsymbol{x})&=-\frac{(\boldsymbol{x}-\boldsymbol{\mu}_i)^T(\boldsymbol{x}-\boldsymbol{\mu}_i)}{2\sigma^2}+\ln p(\omega_i)\\ &=-\frac{\begin{Vmatrix} \boldsymbol{x}-\boldsymbol{\mu}_i \end{Vmatrix}^2}{2\sigma^2}+\ln p(\omega_i) \end{align} \] 其中 \(\begin{Vmatrix} \boldsymbol{x}-\boldsymbol{\mu}_i \end{Vmatrix}\) 是求欧氏距离，即欧几里得范数。

故在此种决策函数下，只需计算 \(\boldsymbol{x}\) 到各类样本均值 \(\boldsymbol{\mu}_i\) 的范数，选择范数最小（在空间中称为距离最近）的类别即可。

情况一也称作最小距离分类器。

对判别函数重整，有 \[ g_i(\boldsymbol{x})=\frac{1}{2\sigma^2}(\begin{Vmatrix}\boldsymbol{x}\end{Vmatrix}^2-2\boldsymbol{\mu}_i^T\boldsymbol{x}+\begin{Vmatrix}\boldsymbol{\mu}\end{Vmatrix}^2)+\ln{p(\omega_i)} \] 其中 \(\begin{Vmatrix}\boldsymbol{x}\end{Vmatrix}^2\) 对于任意 \(i\) 是相等的，于是乎我们可以把上式等价于 \[ g_i(\boldsymbol{x})=\boldsymbol{w}_i^T \boldsymbol{x}+\omega_{i0} \] 其中 \[ \boldsymbol{w}_i=\frac{1}{\sigma ^2}\boldsymbol{\mu}_i\\ \omega_{i0}=-\frac{1}{2\sigma^2}\begin{Vmatrix}\boldsymbol{\mu}\end{Vmatrix}^2+\ln{p(\omega_i)} \] \(\omega_{i0}\) 又称作第 \(i\) 个方向的阈值或偏置。

使用线性判别函数的分类器称为“线性机器”。这类分类器有许多有趣的理论性质。

此处只需注意到一个线性机器的判定面是一些超平面，它们是由两类问题中可获得最大后验概率的线性方程 \(g_i(\boldsymbol{x})=g_j(\boldsymbol{x})\) 来确定。

上式可写为 \[ \boldsymbol{w}^T(\boldsymbol{x}-\boldsymbol{x}_0)=0 \] 其中 \[ \boldsymbol{w}=\boldsymbol{\mu}_i-\boldsymbol{\mu}_j \] 且 \[ \mathbf{x}_{0}=\frac{1}{2}\left(\boldsymbol{\mu}_{i}+\boldsymbol{\mu}_{j}\right)-\frac{\sigma^{2}}{\left\|\boldsymbol{\mu}_{i}-\boldsymbol{\mu}_{j}\right\|^{2}} \ln \frac{P\left(\omega_{i}\right)}{P\left(\omega_{j}\right)}\left(\boldsymbol{\mu}_{i}-\boldsymbol{\mu}_{j}\right) \] 此方程定义了一个通过 \(\boldsymbol{x}_0\) 且与向量 \(\boldsymbol{w}\) 正交的超平面。

如果 \(\sigma^2\) 相对于范数的平方较小，那么判决边界的位置相对于确切的先验概率值并不敏感。

情况二：\(\Sigma_i=\Sigma_j=\Sigma\)

各类方差相同，\(\Sigma_i=\Sigma_j=\Sigma\)

可以证明，此时判别函数仍满足线性关系，即 \[ g_i(\boldsymbol{x})=\boldsymbol{w}_i^T\boldsymbol{x}+\omega_{i0} \]

情况三：\(\Sigma_i\neq \Sigma_j\)

\(\Sigma_i\neq \Sigma_j\)

此时判别函数为 \[ g_i(\boldsymbol{x})=\boldsymbol{x}^TA_i\boldsymbol{x}+\boldsymbol{w}_i^T+\omega_{i0} \] 此分类器为非线性分类器（二次型分类器）。

实际计算

两类高斯分布所计算出的贝叶斯判决边界如下，每一类都基于 4 个数据点。

以 \(\omega_1\) 表示 4 个黑点的集合，\(\omega_2\) 表示红点集合。

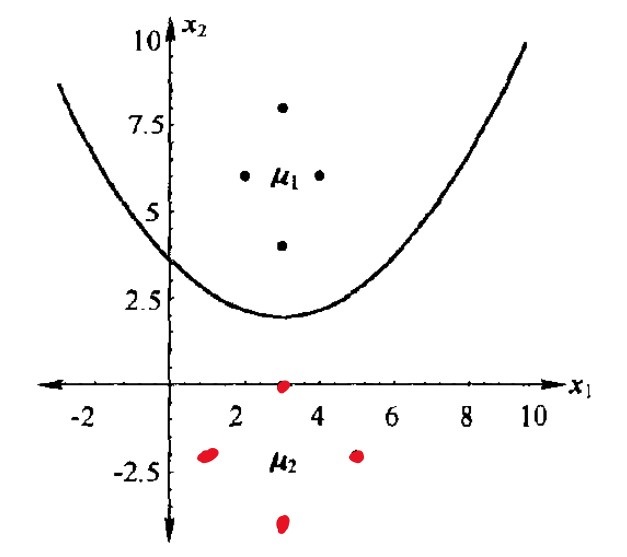
由图可知，\(\omega_1\) 的特征向量矩阵为 \[ X=\begin{bmatrix} 2 & 3 & 3 & 4\\ 6 & 8 & 4 & 6 \end{bmatrix} \] 可知特征向量维度 \(d=2\)

由均值公式 \[ \mu_k=\frac{1}{4}\sum^4_{i=1} x_{ki},k=1,2 \] 得均值向量为 \[ \boldsymbol{\mu}=\begin{bmatrix} 3\\ 6 \end{bmatrix} \] 由协方差公式 \[ \sigma(\boldsymbol{x}_k,\boldsymbol{x}_k)=\frac{1}{n}\sum^n_{i=1}(x_{ki}-\bar{x}_k)^2,k=1,2,\cdots,d \] 得协方差为 \[ \begin{align} \sigma\left(x_{1}, x_{1}\right)&=\frac{1}{4}\left\{\left(x_{11}-\bar{x}_{1}\right)\left(x_{11}-\bar{x}_{1}\right)+\left(x_{12}-\bar{x}_{1}\right)\left(x_{12}-\bar{x}_{1}\right)+\left(x_{13}-\bar{x}_{1}\right)\left(x_{13}-\bar{x}_{1}\right)+\left(x_{14}-\bar{x}_{1}\right)\left(x_{14}-\bar{x}_{1}\right)\right\} \\ &=\frac{1}{4}\{(2-3)(2-3)+(3-3)(3-3)+(3-3)(3-3)+(4-3)(4-3)\}\\ &=\frac{1}{2} \end{align} \]

此处 \(x_1=\begin{bmatrix}2&3&3&6\end{bmatrix},x_{11}=2,x_{12}=3,\bar{x}_1=3\)，同时忽略其他协方差的计算。

同理可得，协方差矩阵为 \[ \Sigma=\begin{bmatrix} \frac{1}{2} & 0\\ 0 & 2 \end{bmatrix} \] 对于另一组特征向量 \[ X=\begin{bmatrix} 1 & 3 & 3 & 5\\ -2 & 0 & -4 & -2 \end{bmatrix} \] 同理可得均值和方差。

记第一组数据的均值为 \(\mu_1\)，协方差矩阵为 \(\Sigma_1\)；第二组数据的均值为 \(\mu_2\)，协方差矩阵为 \(\Sigma_2\)： \[ \boldsymbol{\mu}_1=\begin{bmatrix} 3\\ 6 \end{bmatrix}, \boldsymbol{\mu}_2=\begin{bmatrix} 3\\ -2 \end{bmatrix} \\ \Sigma_1=\begin{bmatrix} \frac{1}{2} & 0\\ 0 & 2 \end{bmatrix}, \Sigma_2=\begin{bmatrix} 2 & 0\\ 0 & 2 \end{bmatrix} \] 可得逆矩为 \[ \Sigma_1^{-1}=\begin{bmatrix} 2 & 0\\ 0 & \frac{1}{2} \end{bmatrix}, \Sigma_2^{-1}=\begin{bmatrix} \frac{1}{2} & 0\\ 0 & \frac{1}{2} \end{bmatrix} \] 假定两类分布的先验概率相等，即 \(P(\omega_1)=P(\omega_2)=0.5\)，代入后可得 \(g_1(\boldsymbol{x})=g_2(\boldsymbol{x})\) 时的判决边界为 \[ x_2=3.514-1.125x_1+0.1875x_1^2 \]

这里由于各类协方差矩阵各不相同，于是套用情况三的公式

实际应用

拼写纠错检查

当用户输入了一个不在字典中的单词，我们需要去猜测：“这个家伙到底真正想输入的单词是什么呢？”用形式化的语言来叙述，就是我们需要求得： \[ P(\text{我们猜测他想输入的单词}|\text{他实际输入的单词}) \] 比如用户输入thew，那么猜测他到底想输入the，还是thaw，还是其他的单词？到底哪一个单词的可能性比较大？这时候我们就可以用贝叶斯去求出每个词语的可能性。

不妨把我们的猜测记为 \(h_1,h_2,\cdots,h_n\)，他们都属于一个有限且离散的猜测空间H（单词总共就只有那么多，\(H\) 代表 hypothesis），将用户实际输入的单词记为 \(D\)（\(D\) 代表 data，即观测数据），于是问题转为：

\(P(\text{我们的猜测1}|\text{他实际输入的单词})\) 可以表示为 \(P(h_1|D)\)，同理对于猜测2，则表示为 \(P(h_2|D)\)，我们需要计算这些概率值，取最大值。

将所有猜测统一记为 \(P(H|D)\)，运用贝叶斯公式可以得到 \[ P(H|D)=\frac{P(H)P(D|H)}{P(D)} \] 由于证据因子 \(P(D)\) 对我们的决策无影响，故计算时将公式简化为 \[ P(H|D)\propto P(H)P(D|H) \] 即用户实际想输入 the 的可能性大小取决于 the 本身在词汇表中被使用的可能性（频繁程度）大小和想打 the 却打成 thew 的可能性大小（似然）的乘积。

抽象理解为给定观测数据，猜测是好是坏取决于“这个猜测本身独立的可能性大小”（先验概率）和“这个猜测生成我们观测到的数据的可能性大小”（似然）的乘积。

有两种模型解决该问题：

最大似然：最符合观测数据的最有优势（即 \(P(D|H)\) 最大）
奥卡姆剃刀：先验概率 \(P(H)\) 较大的模型有较大的优势。

医生诊断

一个两类识别问题：医生根据病人血液中白细胞的浓度来判断病人是否患血液病。

根据医学知识和以往的经验，医生知道（先验知识）：

患病的人，白细胞的浓度服从均值2000，方差1000的正态分布；未患病的人，白细胞的浓度服从均值7000，方差3000的正态分布
一般人群中，患病的人数比例为0.5%

当一个人的白细胞浓度是3100，医生应该做出怎样的判断？

用 \(\Omega\) 表示分类集合，有 \(\omega_1\) 表示患病，\(\omega_2\) 表示未患病；

用 \(x\) 表示"白细胞浓度"这个随机变量，即选择其作为特征。

由先验知识我们可以得到先验概率：

\(P(\omega_1)=0.5\%,P(\omega_2)=99.5\%\)
白细胞浓度在两种类别下的类条件概率密度：\(p(x|\omega_1)\sim N(2000,1000),p(x|\omega_2)\sim N(7000,3000)\)

查表可以得到类条件概率： \[ P(3100|\omega_1)=2.1785\times10^{-4}\\ P(3100|\omega_2)=5.7123\times10^{-5}\\ \] 根据贝叶斯公式，计算得到后验概率： \[ \begin{align} P(\omega_1|3100)&=1.9\%\\ P(\omega_2|3100)&=98.1\% \end{align} \] 故判决为 \(\omega_2\)，即医生诊断为：未患病，体征正常。