模式识别-神经网络笔记

发表于 2023-06-01 更新于 2023-06-19 本文字数： 15k 阅读时长 ≈ 14 分钟

有关神经网络的简要笔记

模式识别

神经网络

神经元模型

神经网络中最基本的成分是神经元（neuron）模型，在 M-P 神经元模型中，每个神经元与 \(n\) 个其他神经元连接（connect），接受 \(n\) 个神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值（偏置）进行比较，然后通过“激活函数”（activation function）处理以产生神经元的输出。

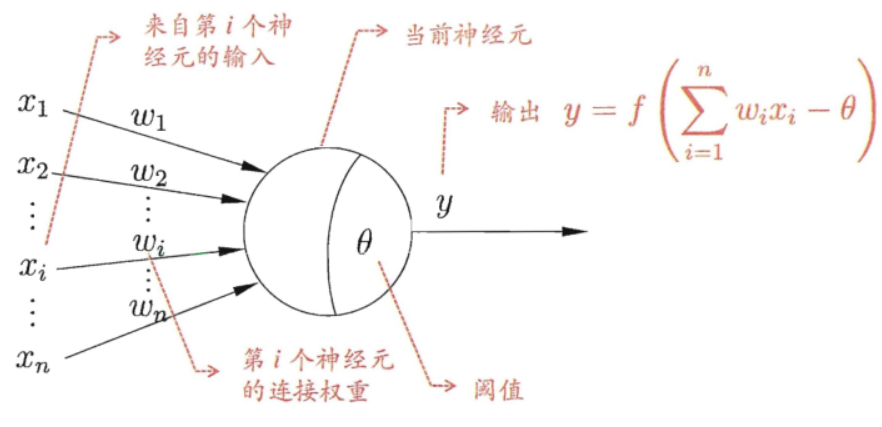
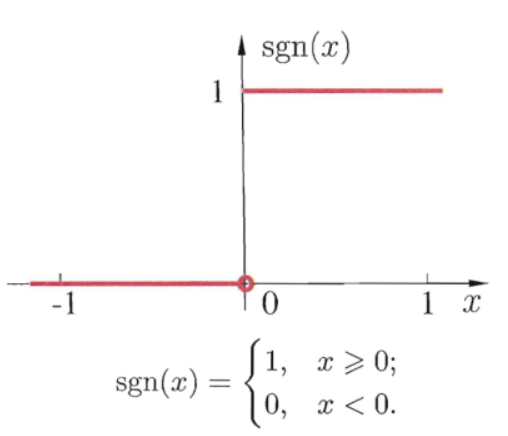
理想值的激活函数是阶跃函数 \(\mathrm{sgn}(x)\)，对于任意输入只有 0 和 1 的输出。

但由于阶跃函数具有不连续，不光滑等不太好的性质，因此常用 Sigmoid 或者 ReLU 函数作为激活函数（对于模型的训练常常使用的是类梯度下降法，而类梯度下降法要求函数必须连续光滑）。

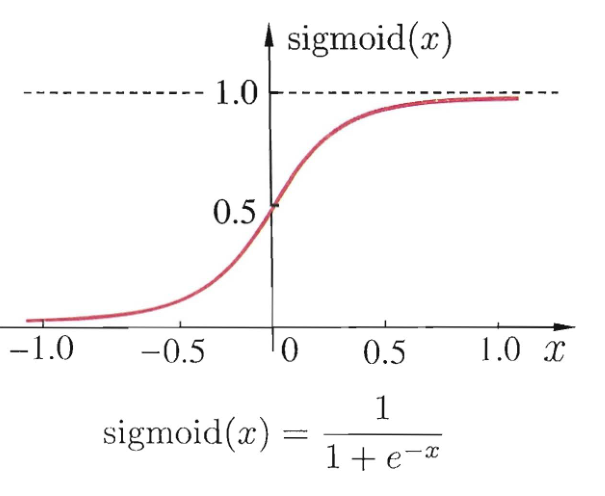
sigmoid 函数又叫挤压函数，它的作用是将任意值挤压到 \([0,1]\) 范围内。

把这样许多个神经元按一定层次结构连接起来，就得到了神经网络。

在现实应用中，往往会选择更合适的 ReLU 函数，即线性修正单元（Rectified Linear Unit），它的梯度仅能取 0 和 1，当输入小于 0 时，梯度为 0；当输入大于 0 时，梯度为 1。

好处是，ReLU 的梯度的连乘不会收敛到 0，连乘的结果也只可能是两个值：0 或 1。

此时，如果梯度值为 1，梯度保持值不变进行前向传播；如果值为 0，梯度从该位置停止前向传播。

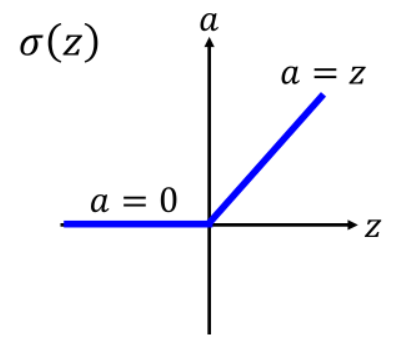
使用 ReLU 的好处是，梯度下降的速度快，而且模型更加仿生，同时可以避免梯度消失或者梯度爆炸问题。

但缺点是，神经元死亡问题。

当 ReLU 函数的输出值为 0 时，ReLU 的导数也为 0，因此会导致 \(\Delta w\) 一直为 0，进而导致 \(w\) 无法被更新，因此会导致这个神经元永久性死亡（一直输出 0）。

感知机

如果我们以神经网络的方式抽象感知器，可以发现它是由两层神经元组成的神经网络，如下图所示。

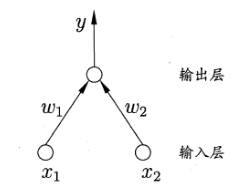
输入层接收外界输入信号后传递给输出层，输出层是 M-P 神经元。

感知机（Perceptron）能容易地实现逻辑与、或、非运算。

与：令 \(w_1=w_2=1,b=-2\)，则 \(y=f(1\cdot x_1+1\cdot x_2-2)\)，仅在 \(x_1=x_2=1\) 时，输出 \(y=1\)
或：令 \(w_1=w_2=1,b=-0.5\)，则 \(y=f(1\cdot x_1+1\cdot x_2-0.5)\)，仅在 \(x_1=11\) 或 \(x_2=1\) 时，输出 \(y=1\)
非：令 \(w_1=-0.6,w_2=0,b=0.5\)，则 \(y=f(-0.6\cdot x_1+0\cdot x_2+0.5)\)，仅在 \(x_1=1\) 时，输出 \(y=1\)；当 \(x_1=0\) 时，输出 \(y=0\)

更一般地，我们可以把阈值（偏置）看作是哑节点（dummy node），即像是线性分类中我们会增广权重矩阵，将偏置放入权重矩阵中，同样的哑节点也是一个固定输入的节点，这样我们就可以只训练权重而不用管阈值（偏置）。

感知机的学习规则非常简单，类似于感知器，对于训练样本 \((\boldsymbol{x},y)\)，若感知机输出为 \(\hat{y}\)（预测输出），则将权重调整 \[ w_i\gets w_i+\Delta w_i\\ \Delta w_i=\eta(y-\hat{y})x_i \] 其中 \(\eta\in (0,1)\) 称为学习率。

可以发现，如果说感知机对训练样本预测正确，即 \(y=\hat{y}\)，则感知器不发生变化；否则将根据错误程度进行权重调整。

我们可以将 \(w_1,w_2\) 写成权重的形式，则可以得知该感知机的分类平面为 \[ g(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+b \] 不难发现，感知机可以处理的问题都是线性可分问题，这与感知器算法相比毫无优势可言。

但感知机是多层神经网络的开始，可以从与、或、非问题中发现，其可以从中提取新特征。

多层网络

一个二输入两层感知机网络，在平面上可以做线性二分类问题。但是在处理非线性问题，如异或问题时，还是难以解决。

以异或问题举例，为了解决该问题，有人提出，一条线无法分类，那么我们使用两条线即可。

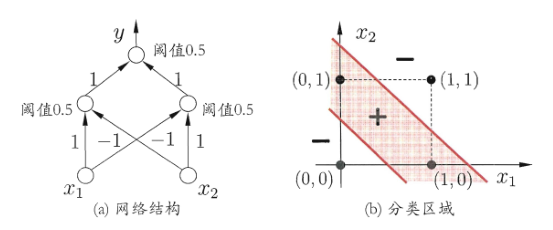
我们引入两个感知机，从两个角度解决原特征无法解决的问题，然后再通过输出层输出结果，这样我们就从单元线性的角度解决了整体非线性问题。

更一般的，常见的多层神经网络是如图所示的层级结构，每层神经元与下一层神经元全连接，神经元之间不存在同层连接也不存在跨层连接（现代神经网络模型中，残差网络 ResNet 存在跨层连接），我们把这样的神经网络模型成为多层前馈神经网络（multi-layer feedforward neural networks）。

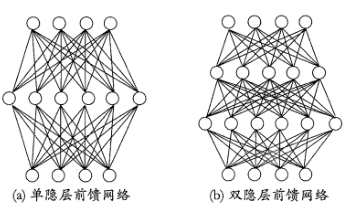
其中输入层神经元接收外界输入，隐层与输出层神经元对信号进行加工，最终结果由输出层神经输出；换言之，输入层神经元仅是接受输入，不进行函数处理，隐层与输出层包含功能神经元。

而神经网络的学习过程，就是根据训练数据来调整神经元之间的连接权重，以及每个功能神经元的阈值（偏置）。

或者说，神经网络学习到的东西都蕴含在连接权重和阈值（偏置）中。

全连接网络

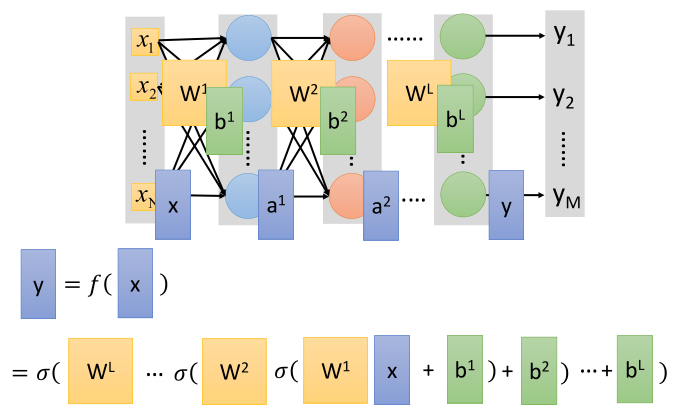
对于多层前馈神经网络，又称作是全连接网络，可以看作如下图所示的结构。

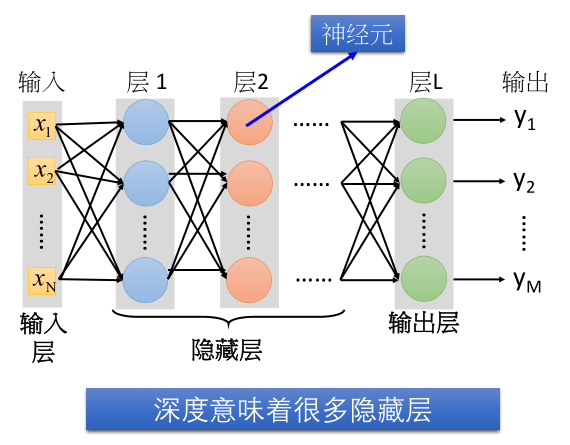
所谓深度网络，是指有许多的隐藏层的神经网络。

一个实际的计算例子示意图为

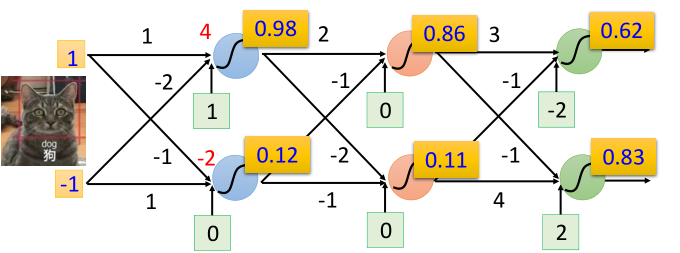
我们可以发现，输入向量 \(\boldsymbol{x}\) 会被传递给第一个隐藏层，然后每个神经元输出一个值，作为新的输入向量传递给下一个隐藏层。

不妨我们给每个神经元都定义一个权重 \(\boldsymbol{w}\) 和偏置 \(b\)，那么对于某一个神经元的输出可以写成 \[ y_i=\sigma(\boldsymbol{w}_i^T\boldsymbol{x}+b_i)=\sigma(z_i) \] 其中 \(\sigma(z)\) 是一个激活函数。

而对于同一个隐藏层，不难发现，如果把一个隐藏层看作是黑盒函数的话，那么它将是一个输入向量、输出向量的向量函数，即 \[ f(\boldsymbol{x})=\boldsymbol{y}=\begin{bmatrix} y_1\\ y_2\\ \vdots\\ y_l \end{bmatrix} \] 例如对于第一个隐藏层可以写作 \[ f(\begin{bmatrix}1\\-1\end{bmatrix})=\begin{bmatrix}\sigma(\boldsymbol{w}_1^T\boldsymbol{x}+b_1)\\\sigma(\boldsymbol{w}_2^T\boldsymbol{x}+b_2)\end{bmatrix}=\begin{bmatrix}\sigma(4)\\\sigma(-2)\end{bmatrix}=\begin{bmatrix}0.98\\0.12\end{bmatrix} \] 我们不妨以层为单位建立数学模型，可以发现每一层拥有一个权重矩阵和偏置向量。权重矩阵由同一层的所有神经元的权重向量组成，偏置向量由同一层的所有神经元的偏置组成。

即对于一个隐藏层，有偏置矩阵和偏置向量 \[ W=\begin{bmatrix} \boldsymbol{w}_1\\ \boldsymbol{w}_2\\ \vdots\\ \boldsymbol{w}_l \end{bmatrix},\boldsymbol{b}=\begin{bmatrix} b_1\\ b_2\\ \vdots\\ b_l \end{bmatrix} \] 那么一个隐藏层所代表的数学模型为 \[ f(\boldsymbol{x})=\sigma(W\boldsymbol{x}+\boldsymbol{b}) \] 这是一个向量函数，输入一个向量，输出一个向量。其中 \(\sigma\) 函数代表对每一行的值进行激活。

有时为了训练的方便，我们也会对输入向量进行增广化，使得偏置向量与权重矩阵堆叠，即 \[ f(\boldsymbol{x})=\begin{bmatrix}W\\\boldsymbol{b}\end{bmatrix}\begin{bmatrix}\boldsymbol{x}\\1\end{bmatrix}=A\begin{bmatrix}\boldsymbol{x}\\1\end{bmatrix} \] 其中， \[ A=\begin{bmatrix} \boldsymbol{w}_1\\ \boldsymbol{w}_2\\ \vdots\\ \boldsymbol{w}_l\\ \boldsymbol{b} \end{bmatrix} \] 基于 numpy 我们可以写出代码

Layer 神经网络层级描述代码

import numpy as np
from typing import Protocol

class Activation(Protocol):
    def active(self, x: np.float64) -> np.float64:
        ...
    
    def diff(self, x: np.float64) -> np.float64:
        ...

class Sigmoid:
    """
    激活函数 1/(1+e^(-x))
    """
    def active(self, x: np.float64) -> np.float64:
        return 1 / (1 + np.exp(-x))

    def diff(self, x: np.float64) -> np.float64:
        return self.active(x) * (1 - self.active(x))

class ReLU:
    """
    线性激活单元
    """
    def active(self, x: np.float64) -> np.float64:
        y = x
        y[x <= 0] = np.float64(0)
        return y

    def diff(self, x: np.float64) -> np.float64:
        y = np.ones(x.size, x.dtype)
        y[x <= 0] = np.float64(0)
        return y

class Layer:
    """
    神经网络层级类
    属性：
        weight: 该层级的权重矩阵，由该层级所包含的神经元的权重组成
        bias: 该层级的偏置向量，由该层级所包含的神经元的偏置组成
        activation: 该神经网络层级的所有神经元的激活函数
        eta: 学习率
        _next: 该层级所连接的下一层级
        _prev: 该层级所连接的上一层级
        _in: 该层级的上一次输入
        _out: 该层级的上一次输出
    """
    weight: np.ndarray
    bias: np.ndarray
    activation: Activation
    eta: np.float64
    _next: 'Layer'
    _prev: 'Layer'
    _in: np.ndarray
    _out: np.ndarray

    def __init__(self, weight: np.ndarray, bias: np.ndarray, _next: 'Layer' = None, _prev: 'Layer' = None, activation: Activation = Sigmoid(), eta: np.float64 = 1) -> None:
        """
        参数：
            weight: 该层级的权重矩阵，一个二维矩阵
                    第一个维度代表不同的神经元，第二个维度代表来自哪个神经元的输入
            bias: 该层级的偏置向量，一个向量
        """
        self.weight = np.array(weight, dtype = np.float64)
        self.bias = np.array(bias, dtype = np.float64)
        self._next = _next
        if _next is not None:
            self._next._prev = self
        self._prev = _prev
        if _prev is not None:
            self._prev._next = self
        self.activation = activation
        self.eta = eta
        self._in = np.array([], dtype = np.float64)
        self._out = np.array([], dtype = np.float64)

    def forward(self, x: np.ndarray):
        """
        正向传播
        参数：
            x: 输入向量
        """
        self._in = np.array(x, dtype = np.float64)
        self._out = self.activation.active(np.dot(self.weight, self._in) + self.bias)
        if self._next is not None:
            self._next.forward(self._out)
        return self
    
    def backward(self, delta: np.ndarray):
        """
        反向传播
        参数：
            delta: 误差
        """
        diff = self.activation.diff(np.dot(self.weight, self._in) + self.bias)
        if self._prev is not None:
            self._prev.backward(np.dot(self.weight.T, (delta * diff)))
        self.weight = self.weight - self.eta * np.dot((diff * delta).reshape(-1, 1), self._in.reshape((1, -1)))

    def __repr__(self):
        return f"Layer(weight={self.weight}, bias={self.bias}, in={self._in}, out={self._out}, activation={self.activation.__class__})"

Network 神经网络描述代码

class Network:
    """
    神经网络类
    属性：
        layers: 该神经网络所包含的所有层级
        _in: 该神经网络的上次输入
        _out: 该神经网络的上次输出
    """
    head_layer: Layer
    tail_layer: Layer

    def __init__(self, head_layer: Layer, tail_layer: Layer = None) -> None:
        """
        参数：
            head_layer: 该神经网络的第一个神经元层级
            tail_layer: 该神经网络的最后一个神经元层级（输出层级）
        """
        self.head_layer = head_layer
        if tail_layer is None:
            self.tail_layer = head_layer
            while self.tail_layer._next is not None:
                self.tail_layer = self.tail_layer._next
        else:
            self.tail_layer = tail_layer
        self._in = np.array([], dtype = np.float64)
        self._out = np.array([], dtype = np.float64)

    @classmethod
    def create(cls, layers: list[Layer]):
        """
        根据给定的层级参数，创建一个神经网络
        参数：
            layer_args: 给定的层级参数，每一个元素都是一个元组，元组元素为(权重矩阵，偏置向量)
        """
        head_layer = layers[0]
        layer = head_layer
        for l in layers[1:]:
            l._prev = layer
            layer._next = l
            layer = l
        return cls(head_layer, layer)
    
    @property
    def layers(self):
        """
        神经元的所有层级列表
        """
        _layers = [self.head_layer]
        while _layers[-1]._next is not None:
            _layers.append(_layers[-1]._next)
        return _layers

    def error(self, x: np.ndarray, y: np.ndarray):
        """
        获取该输入输出在该网络的均方误差
        """
        self.head_layer.forward(x)
        E = self.tail_layer._out - y
        return np.dot(E, E) / 2

    def forward(self, x: np.ndarray):
        """
        正向传播
        参数：
            x: 输入向量
        """
        self._in = np.array(x, dtype = np.float64)
        self.head_layer.forward(self._in)
        self._out = self.tail_layer._out
        return self._out
    
    def out_list(self):
        """
        获取所有层级的上一次输出
        """
        layer = self.head_layer
        out = []
        while layer is not None:
            out.append(layer._out)
            layer = layer._next
        return out
    
    def back_propagate(self, x: np.ndarray, y: np.ndarray):
        """
        反向传播
        参数：
            x: 输入向量
            y: 预期输出向量
        """
        x = np.array(x, dtype = np.float64)
        y = np.array(y, dtype = np.float64)
        self.head_layer.forward(x)
        E = self.tail_layer._out - y
        self.tail_layer.backward(E)
        return self
            
    def __repr__(self):
        _repr = f"Network(head_layer={self.head_layer}, tail_layer={self.tail_layer}, in={self._in}, out={self._out})"
        return _repr

其中使用 weight 描述权重矩阵，bias 描述偏置向量，_next 表示与该层连接的下一层，_prev 表示与该层连接的上一层。

在这里我们只关注正向传播算法，根据以上理论，输入一个向量 \(x\)，那么将输出权重矩阵乘以输入加上偏置的结果。

def forward(self, x: np.ndarray):
    """
    正向传播
    参数：
        x: 输入向量
    """
    self._in = np.array(x, dtype = np.float64)
    self._out = self.activation.active(np.dot(self.weight, x) + self.bias)
    if self._next is not None:
        self._next.forward(self._out)
    return self

如上代码，接受的输入向量将与该层的权重矩阵相乘，加上偏置后使用激活函数进行激活，得到该层的输出；如果该层与其他层相连接，那么将该层的输出作为下一层的输入传播下去；直到该层为最终层（输出层），结束传播。

我们通过代码创建一个三层的神经网络（不计算输入层），其中 create 的参数为一个列表，列表中每个元素都应该是一个二元元组，二元元组由每一层的权重矩阵和偏置组成，作为神经网络的参数。

network = Network.create([
    ([[1, -2], [-1, 1]], [1, 0]),
    ([[2, -1], [-2, -1]], [0, 0]),
    ([[3, -1], [-1, 4]], [-2, 2])
])

我们使用向量 (1,-1) 进行正向传播，结果与理论相符。

x = [1, -1]
network.forward(x)
print(network.out_list())
"""
[array([0.98201379, 0.11920292]), array([0.86351831, 0.11073744]), array([0.61770478, 0.82912398])]
"""

其中，out_list 函数是获取神经网络中层与层之间传递的输出向量。

对于整一个神经网络，我们也可以看作是一个向量函数，内部层与层做线性运算，即 \[ f(\begin{bmatrix}1\\-1\end{bmatrix})=\begin{bmatrix}0.62\\0.83\end{bmatrix},f(\begin{bmatrix}0\\0\end{bmatrix})=\begin{bmatrix}0.51\\0.85\end{bmatrix} \] 神经元的堆叠

反向传播算法

更新策略

在感知器模型中，我们会使用梯度下降算法来训练我们的模型，但神经网络是一个参数庞大的模型，如果正向的对所有神经元都计算梯度，那么毫无疑问计算量是巨大的。

为了更高效的计算梯度，我们使用反向传播算法（backpropagation）。

首先我们通过正向传播，我们可以得到我们的输出值（预测值）\(\hat{\boldsymbol{y}}\)，我们的目标是使输出值（预测值） \(\hat{\boldsymbol{y}}\) 与目标值（样本值）\(\boldsymbol{y}\) 相接近，使得神经网络可以正确地将输入映射到输出。

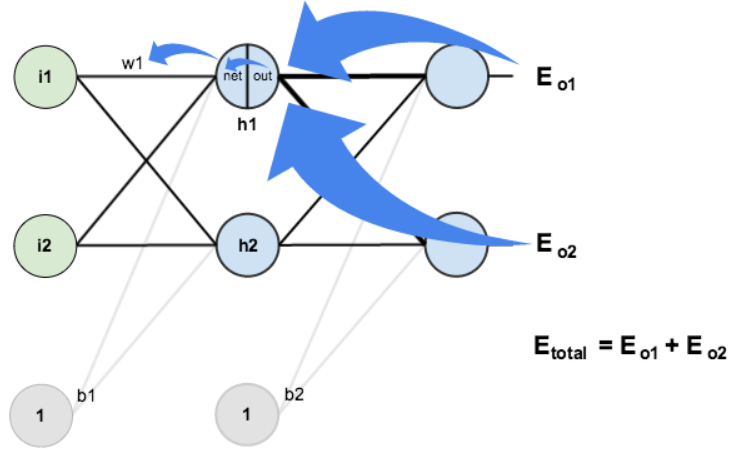
例如对于下图网络，我们输入向量 \((0.05,0.10)\)，网络输出向量 \((0.75,0.77)\)，但我们想要它输出目标向量 \((0.01,0.99)\)。

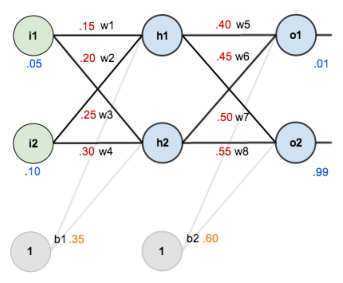
那么首先我们需要定义一个误差函数（损失函数），用于判断输出与目标的偏差，一般使用最常见的均方根误差函数 \[ E=\frac{1}{2}\sum^l_{i=1}(\hat{y}_i-y_i)^2=\frac{1}{2}(\hat{\boldsymbol{y}}-\boldsymbol{y})^T(\hat{\boldsymbol{y}}-\boldsymbol{y}) \] 其中 \(\hat{y}_i,y_i\) 代表向量 \(\hat{\boldsymbol{y}},\boldsymbol{y}\) 的第 \(i\) 个元素。

独立看待第 \(i\) 个输出的均方根误差函数，可以写成 \[ E_i=\frac{1}{2}(\hat{y}_i-y_i)^2 \] 以下推导部分，仅对向量的第 \(k\) 个元素指明小标，常量忽略小标。

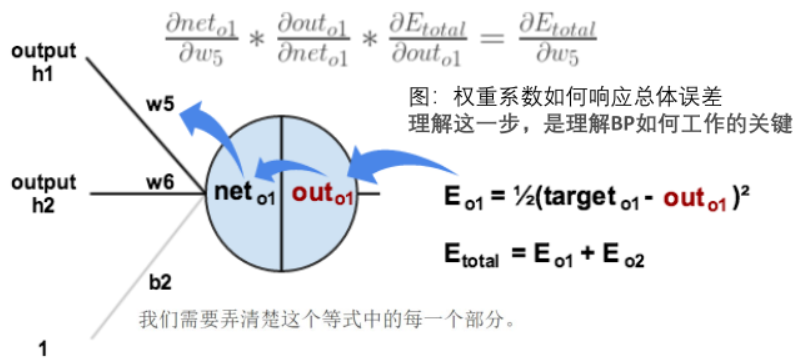
反向传播算法基于梯度下降策略，对于某一个连接权重而言，我们有 \[ w_k\gets w_k+\Delta w_k\\ \Delta w_k=-\eta\frac{\partial E}{\partial w_k} \] 输出层的计算

求误差对权重的梯度，那么根据链式法则，有 \[ \frac{\partial E}{\partial w_k}=\frac{\partial E}{\partial y}\frac{\partial y}{\partial z}\frac{\partial z}{\partial w_k} \]

单个输出的误差受该神经元的输出影响；该神经元的输出受激活函数的输入影响；激活函数的输入受权重（和偏置）的影响。

其中 \[ \frac{\partial E}{\partial y}=-(\hat{y}-y) \] 在输出时即可确定这个值； \[ y=\sigma(\boldsymbol{w}^T\boldsymbol{x}+b)=\sigma(z)\\ \frac{\partial y}{\partial z}=\frac{\partial \sigma}{\partial z}=\sigma'(z) \] 在正向传播时就可以确定这个值； \[ z=\boldsymbol{w}^T\boldsymbol{x}+b\\ \frac{\partial z}{\partial w_k}=x_k \] 即输入向量各分量之和。

那么，误差对权重的梯度即为 \[ \frac{\partial E}{\partial w_k}= -(\hat{y}-y)\sigma'(z)x_k \] 不妨定义 \(\delta=-(\hat{y}-y)=y-\hat{y}\)，即误差对权重的梯度可以写为 \[ \frac{\partial E}{\partial w_k}= \delta\sigma'(z)x_k \] 考虑到对于每一个神经元，都有权重向量 \[ \boldsymbol{w}=\begin{bmatrix} w_1\\ w_2\\ \vdots\\ w_l \end{bmatrix} \] 那么单个神经元的输出误差对其权重向量的梯度可以写为 \[ \frac{\partial E}{\partial \boldsymbol{w}}=\begin{bmatrix} \frac{\partial E}{\partial w_1}\\ \frac{\partial E}{\partial w_2}\\ \vdots\\ \frac{\partial E}{\partial w_l} \end{bmatrix} =\begin{bmatrix} \delta\sigma'(z)x_1\\ \delta\sigma'(z)x_2\\ \vdots\\ \delta\sigma'(z)x_l\\ \end{bmatrix} \] 其中 \(\sigma'(z)=\sigma'(\boldsymbol{w}^T\boldsymbol{x}+b)\)。

而一个神经层级的输出误差可以写成 \[ \boldsymbol{E}=\begin{bmatrix} E_1\\ E_2\\ \vdots\\ E_l \end{bmatrix} \] 那么其的误差可以定义为 \[ \Delta=\begin{bmatrix} \delta_1\\ \delta_2\\ \vdots\\ \delta_l \end{bmatrix} =\begin{bmatrix} y_1-\hat{y}_1\\ y_2-\hat{y}_2\\ \vdots\\ y_l-\hat{y}_l \end{bmatrix} \] 那么一个神经层级的输出误差对其权重的梯度可以写为 \[ \frac{\partial \boldsymbol{E}}{\partial W}=\begin{bmatrix} \frac{\partial E_1}{\partial \boldsymbol{w}^T_1}\\ \frac{\partial E_2}{\partial \boldsymbol{w}^T_2}\\ \vdots\\ \frac{\partial E_l}{\partial \boldsymbol{w}^T_l} \end{bmatrix} =\begin{bmatrix} \delta_1\sigma'(z_1)x_{1}& \delta_1\sigma'(z_1)x_{2}& \cdots& \delta_1\sigma'(z_1)x_{l}\\ \delta_2\sigma'(z_2)x_{1}& \delta_2\sigma'(z_2)x_{2}& \cdots& \delta_2\sigma'(z_2)x_{l}\\ \vdots&\vdots&\vdots&\vdots\\ \delta_l\sigma'(z_l)x_{1}& \delta_l\sigma'(z_l)x_{2}& \cdots& \delta_l\sigma'(z_l)x_{l} \end{bmatrix} \] 结果是一个跟权重矩阵同大小的矩阵，梯度矩阵的每一行是对每个神经元权重向量的更新，每一列是对上一层连接权重的更新。

误差逆传递

我们从上面的推导可以发现，梯度下降法中的重点是求解 \(\delta\)，这是因为 \(\sigma'(z)\) 和 \(x\) 都可以在正向传播中求得，而 \(\delta\) 却不行。

\(\delta=y-\hat{y}\)，即神经元输出减去对这个神经元的预期输出，显然，除了输出层神经元的预期输出是我们确定的以外，我们无法直接获取到隐藏层的神经元预期输出。

为了获取到隐藏层的误差，我们需要做一些数学推导。

首先需要明确的是，我们仅需要误差 \(\delta\) 而非 \(E,\hat{y}\)。

考虑单一隐藏层神经元，我们有 \[ \frac{\partial E}{\partial w_k}=\frac{\partial E}{\partial y}\frac{\partial y}{\partial z}\frac{\partial z}{\partial w_k} \] 但是特别的是，这里的隐藏神经元的误差由下一层的误差影响，即 \[ \frac{\partial E}{\partial y}=\frac{\partial (E_1+E_2+\cdots+E_l)}{\partial y} \]

注意，这里的用词是影响而非等于，所以仅仅是偏导相等。

其中，\(E_1,E_2,\cdots,E_l\) 是下一层的误差函数。

那么根据链式法则肯定有 \[ \frac{\partial E_i}{\partial y}=\frac{\partial E_i}{\partial z_i}\frac{\partial z_i}{\partial y} \] 其中，\(z_i=\boldsymbol{w}^T\boldsymbol{y}+b\)，\(y\) 是 \(\boldsymbol{y}\) 的其中一个元素（忽略了小标），\(z_i\) 是对于下一层第 \(i\) 个神经元的网络输入（乘以权重后的）。

下一层神经元的输出误差受下一层神经元的输入影响；下一层神经元的输入受该层神经元的输出影响。

那么有 \[ \frac{\partial E_i}{\partial z_i}=-(\hat{y}_i-y_i)\sigma'(z_i)=\delta_i\sigma'(z_i)\\ \frac{\partial z_i}{\partial y}=w_i \] 输出误差对输入的梯度可以由更新策略中的推导得到，而下一层的网络输入对这一层的输出的梯度是这两个神经元连接的权重系数。

那么 \[ \frac{\partial E_i}{\partial y}=\delta_i\sigma'(z_i)w_i\\ \frac{\partial E}{\partial y}=\delta_1\sigma'(z_1)w_1+\delta_2\sigma'(z_2)w_2+\cdots+\delta_l\sigma'(z_l)w_l \] 我们发现，下一层的误差被乘以权重和导数来反向传播到上一层了，故这也是为什么反向传播算法又称作误差逆传播算法。

总结

在神经网络中，每一层都可以看作是一个向量函数 \(f(\boldsymbol{x})=W\boldsymbol{x}+\boldsymbol{b}\)，我们不妨记每一层（隐藏层与输出层）依次为 \(f_1(\boldsymbol{x}),f_2(\boldsymbol{x}),\cdots,f_d(\boldsymbol{x})\)，其中 \(d\) 为网络深度；每一层的权重矩阵和偏置向量为 \(W_1,W_2,\cdots,W_d\) 和 \(\boldsymbol{b}_1,\boldsymbol{b}_2,\cdots,\boldsymbol{b}_d\)。

权重矩阵由同一层的所有神经元的权重向量组成，偏置向量由同一层的所有神经元的偏置组成。

即对于一个隐藏层，有偏置矩阵和偏置向量 \[ W=\begin{bmatrix} \boldsymbol{w}_1\\ \boldsymbol{w}_2\\ \vdots\\ \boldsymbol{w}_l \end{bmatrix},\boldsymbol{b}=\begin{bmatrix} b_1\\ b_2\\ \vdots\\ b_l \end{bmatrix} \] 我们有 \[ \boldsymbol{y}_1=f_1(\boldsymbol{x})\\ \boldsymbol{y}_2=f_2(\boldsymbol{y}_1)\\ \vdots\\ \boldsymbol{y}_d=f_d(\boldsymbol{y}_{d-1}) \] 其中，\(\boldsymbol{y}_d\) 即是神经网络的输出，以上行为即正向传播。

记输出层误差为 \(\boldsymbol{\delta}_d=\boldsymbol{y}_d-\boldsymbol{y}\)，其中 \(\boldsymbol{y}\) 为目标输出向量。

那么误差向前传递，\(\boldsymbol{\delta}_i=W_{i+1}^T\boldsymbol{\delta}_{i+1}\)，其中 \(i=0,1,\cdots,d-1\)。

权重矩阵从输出层向前递归，更新策略为 \[ W'_i=W_i+\eta\Delta W_i\\ \Delta W_i=\boldsymbol{\delta}_i\sigma'(\boldsymbol{z})\boldsymbol{x}_i\\ \sigma'(\boldsymbol{z}) =\begin{bmatrix} \sigma'(z_1)\\ \sigma'(z_2)\\ \vdots\\ \sigma'(z_l)\\ \end{bmatrix}\\ \] 在代码中，对于每一层写有 backward 函数，用于传递误差更新权重矩阵。

def backward(self, delta: np.ndarray):
    """
    反向传播
    参数：
        delta: 误差
    """
    diff = self.activation.diff(np.dot(self.weight, self._in) + self.bias)
    if self._prev is not None:
        self._prev.backward(np.dot(self.weight.T, (delta * diff)))
    self.weight = self.weight - self.eta * np.dot((diff * delta).reshape(-1, 1), self._in.reshape((1, -1)))

其中 delta 为误差值 \(\boldsymbol{\delta}\)，diff 为 \(\sigma'(\boldsymbol{z})\)。