SM系列算法

发表于 2023-05-01 更新于 2023-05-26 本文字数： 17k 阅读时长 ≈ 15 分钟

有关国密公布的SM系列算法的简要笔记

SM 系列算法

SM2

SM2 是椭圆曲线公钥密码算法，是基于 ECC 的非对称加密，又称作 SM2-ECDSA，主要应用于数字签名。

国密算法标准中推荐使用的默认值为

p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
Gx = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
Gy = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0

其中 \(p\) 为有限域规模，\((a,b)\) 为椭圆曲线参数，\(n\) 为这个椭圆曲线的阶数，\(G(G_x,G_y)\) 为基点。

国密标准规范来源：https://www.sca.gov.cn/sca/xxgk/2010-12/17/content_1002386.shtml

SM2公钥加密算法

符号

\(klen\) 指代消息长度，\(M\) 指代消息，标准推荐 \(\mathrm{KDF}\) 使用 SM3 算法，标准推荐 \(\mathrm{Hash}\) 使用 SM3 算法（输出必须为 32 字节），\(||\) 表示比特串拼接。

公钥与密钥

私钥 \(d\) 是 32 byte（256 bit）的随机数
公钥 \(P=d\cdot G\)

加密

产生随机数 \(k\in[1,n-1]\)
计算椭圆曲线点 \(C_1(x_1,y_1)=k\cdot G\)
计算椭圆曲线点 \(k\cdot P=(x_2,y_2)\)
计算 \(t=\mathrm{KDF}(x_2||y_2,klen)\)，如果 \(t\) 全为 0 比特串，则回到步骤一重新选取 \(k\)
计算椭圆曲线点 \(C_2=M\oplus t\)
计算椭圆曲线点 \(C_3=\mathrm{Hash}(x_2||M||y_2)\)
输出密文 \(C=C_1||C_2||C_3\)

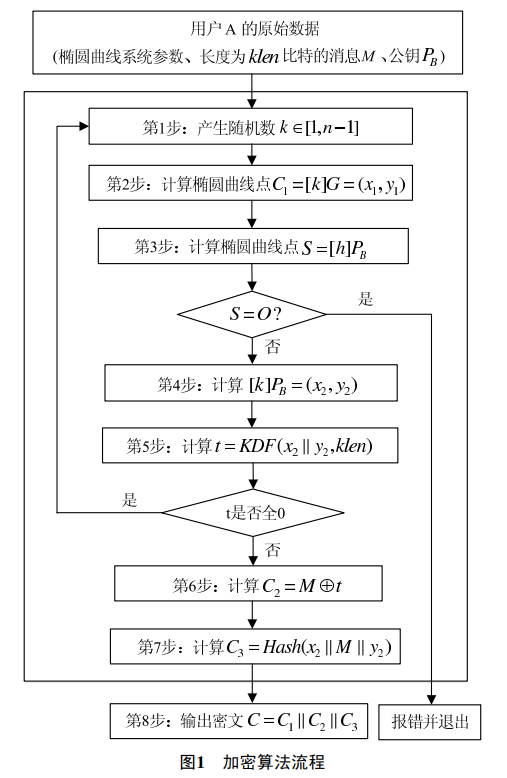
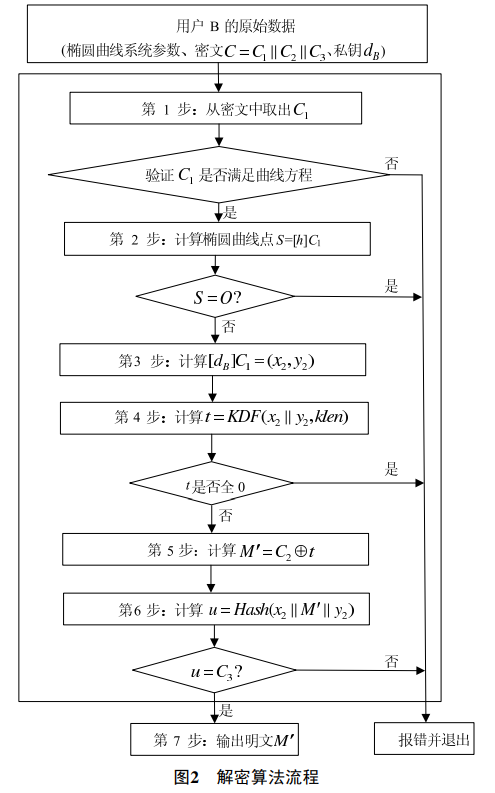
解密

从密文中获取 \(C_1\)，验证 \(C_1\) 是否满足曲线方程，不满足则报错推出
计算椭圆曲线点 \(dC_1=(x_2,y_2)\)
计算 \(t=\mathrm{KDF}(x_2||y_2,klen)\)，如果 \(t\) 全为 0 比特串，则报错退出
计算 \(M'=C_2\oplus t\)
计算 \(u=\mathrm{Hash}(x_2||M'||y_2)\)，验证 \(u=C_3\)，不正确则报错退出
输出明文 \(M'\)

代码

基于 Sagemath 的椭圆曲线的运算代码如下

from . import sm3
from typing import overload, Union
import random
from sage.rings.finite_rings.all import *
from sage.schemes.elliptic_curves.all import *

default_p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
default_n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
default_a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
default_b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
default_Gx = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
default_Gy = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0

def cathex(a: Union[int, bytes], b: Union[int, bytes], *args, byte_size = 32):
    """
    将多个字节串连接打包成 bytes
    """
    if not isinstance(a, bytes):
        a = int(a).to_bytes(byte_size, 'big')
    if not isinstance(b, bytes):
        b = int(b).to_bytes(byte_size, 'big')
    rst = a + b
    for c in args:
        if not isinstance(c, bytes):
            c = int(c).to_bytes(byte_size, 'big')
        rst += c
    return rst

class SM2:
    @overload
    def __init__(self, key: int, p: int = default_p, a: int = default_a, b: int = default_b, G: tuple[int, int] = (default_Gx, default_Gy), n: int = default_n):
        """
        SM2构造函数
        参数：
            private_key: 私钥
            p: 模数
            a: 椭圆曲线参数
            b: 椭圆曲线参数
            G: 基点
            n: 椭圆曲线阶数
        """
        ...
    
    @overload
    def __init__(self, key: tuple[int, int], p: int = default_p, a: int = default_a, b: int = default_b, G: tuple[int, int] = (default_Gx, default_Gy), n: int = default_n):
        """
        SM2构造函数
        参数：
            public_key: 公钥
            p: 模数
            a: 椭圆曲线参数
            b: 椭圆曲线参数
            G: 基点
            n: 椭圆曲线阶数
        """
        ...
    
    def __init__(self, key, p: int = default_p, a: int = default_a, b: int = default_b, G: tuple[int, int] = (default_Gx, default_Gy), n: int = default_n):
        self.__p = p
        self.__a = a
        self.__b = b
        self.__GF = GF(p)
        self.__E = EllipticCurve(self.__GF, [a, b])
        self.__E.set_order(n)
        if G is None:
            self.__G = self.__E.random_point()
        else:
            self.__G = self.__E(G)
        if type(key) is tuple:
            self.__private_key = None
            self.__public_key = self.__E(key)
        else:
            self.__private_key = key
            self.__public_key = self.__private_key * self.__G
    
    @property
    def private_key(self):
        """
        椭圆曲线私钥
        """
        return self.__private_key
    
    @property
    def d(self):
        """
        椭圆曲线私钥
        """
        return self.__private_key
    
    @property
    def public_key(self):
        """
        椭圆曲线公钥
        """
        return self.__public_key
    
    @property
    def P(self):
        """
        椭圆曲线公钥
        """
        return self.__public_key
    
    @property
    def a(self):
        """
        椭圆曲线参数
        """
        return self.__a
    
    @property
    def b(self):
        """
        椭圆曲线参数
        """
        return self.__b
    
    @property
    def p(self):
        """
        椭圆曲线模数
        """
        return self.__p

    @property
    def GF(self):
        """
        椭圆曲线有限域
        """
        return self.__GF
    
    @property
    def order(self):
        """
        椭圆曲线阶数
        """
        return self.E.order()
        
    @property
    def E(self):
        """
        椭圆曲线
        """
        return self.__E

    @property
    def G(self):
        """
        椭圆曲线基点
        """
        return self.__G

    def encrypt(self, M: bytes, k0: int = None):
        """
        椭圆曲线公钥加密
        参数：
            M: 消息
            k0: 指定加密随机数
        返回值：
            密文C=C1||C2||C3
        """
        klen = len(M)
        while True:
            if k0 is None:
                k = random.randint(1, self.order - 1)
            else:
                k = k0
                k0 = None
            C1 = k * self.G
            T1 = k * self.P
            t = sm3.KDF(cathex(T1[0], T1[1]), klen)
            if any(i > 0 for i in t):
                break
        C2 = [(Mi ^ ti) for Mi, ti in zip(M, t)]
        C3 = sm3.hash(cathex(T1[0], M, T1[1]))
        C = cathex(b"\x04", C1[0], C1[1], bytes(C2), C3)
        return C
    
    def decrypt(self, C: bytes):
        """
        椭圆曲线公钥解密
        参数：
            C: 以C1||C2||C3形式拼接的密文
        返回值：
            明文消息
        """
        if C[0] != 0x04:
            raise RuntimeError('SM2的密文起始必须是0x04')
        C = C[1:]
        klen = len(C) - 96
        C1 = (int.from_bytes(C[:32], 'big'), int.from_bytes(C[32:64], 'big'))
        if C1 not in self.E:
            raise RuntimeError('SM2的密文C1点必须是椭圆上的点')
        C1 = self.E(C1)
        C2 = C[64:-32]
        C3 = C[-32:]
        T1 = self.d * C1
        t = sm3.KDF(cathex(T1[0], T1[1]), klen)
        if all(i == 0 for i in t):
            raise RuntimeError('SM2的KDF计算结果错误')
        M = [(Ci ^ ti) for Ci, ti in zip(C2, t)]
        M = bytes(M)
        u = sm3.hash(cathex(T1[0], M, T1[1]))
        if u != C3:
            raise RuntimeError('SM2消息哈希验证错误')
        return M

SM2数字签名算法

符号

\(M\) 指代消息，标准推荐 \(\mathrm{KDF}\) 使用 SM3 算法，标准推荐 \(\mathrm{Hash}\) 使用 SM3 算法（输出必须为 32 字节）。

公钥与密钥

私钥 \(d\)
公钥 \(P=d\cdot G\)

用户信息

签名者具有可辨别标识 \(ID\)，记 \(ENTL\) 是可辩别表示的比特大小（占两字节），使用杂凑算法生成 32 字节的杂凑值 \(Z\)。标准推荐使用 SM3 算法作为杂凑算法。 \[ Z=\mathrm{Hash}(ENTL||ID||a||b||G_x||G_y||P_{x}||P_{y}) \]

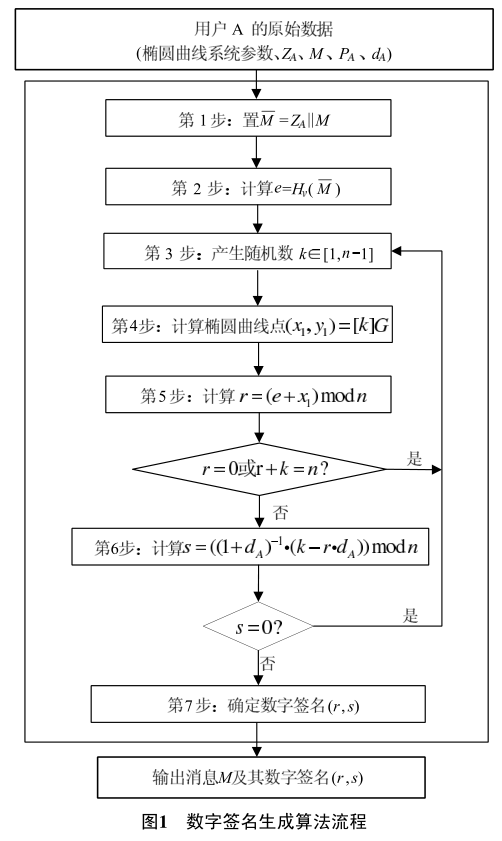
签名

计算 \(e=\mathrm{Hash}(Z||M)\)
产生随机数 \(k\in[1,n-1]\)
计算椭圆曲线点 \((x_1,y_1)=k\cdot G\)
计算 \(r=e+x_1\pmod{n}\)，若 \(r=0\) 或 \(r+k=n\) 则重新选取随机数
计算 \(s=(1+d)^{-1}\cdot(k-r\cdot d)\pmod{n}\)，若 \(s=0\) 则重新选取随机数
输出消息 \(M\) 的签名 \((r,s)\)

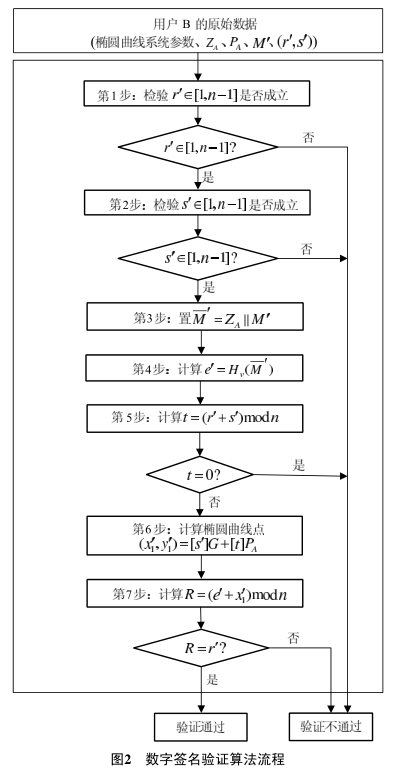
验证

接收到消息 \(M'\) 和数字签名 \((r',s')\)。

检验 \(r',s'\in[1,n-1]\)，如果错误则验证失败
计算 \(e'=\mathrm{Hash}(Z||M')\)
计算 \(t=r'+s'\pmod{n}\)，如果 \(t=0\) 则验证失败
计算椭圆曲线点 \((x_1',y_1')=s'G+tP\)
计算 \(R=e'+x_1'\pmod{n}\)，如果 \(R=r'\) 则验证通过；否则验证失败。

代码

def sign(self, e: bytes, k0: int = None):
    """
    椭圆曲线签名生成
    参数：
        e: 数据产生的哈希值
        k0: 指定加密随机数
    返回值：
        签名(r, s)
    """
    while True:
        if k0 is None:
            k = random.randint(1, self.order - 1)
        else:
            k = k0
            k0 = None
        T = k * self.G
        r = (int.from_bytes(e, 'big') + int(T[0])) % self.order
        if r == 0 or r + k == self.order:
            continue
        s = inverse_mod(1 + self.d, self.order) * (k - r * self.d) % self.order
        if s == 0:
            continue
        return (r, s)

def ZHash(self, ID: bytes):
    """
    产生32字节的杂凑值Z
    输入：
        ID: 可辩别标识
    输出：
        32字节的杂凑值Z
    """
    ENTL = len(ID) * 8
    return sm3.hash(cathex(int(ENTL).to_bytes(2, 'big'), ID, self.a, self.b, self.G[0], self.G[1], self.P[0], self.P[1]))

def raw_sign(self, M: bytes, ID: bytes, k0: int = None):
    """
    椭圆曲线签名生成
    参数：
        M: 消息
        ID: 可辩别标识
        k0: 指定加密随机数
    返回值：
        签名(r, s)
    """
    Z = self.ZHash(ID)
    e = sm3.hash(Z + M)
    return self.sign(e, k0)
    
def verify(self, e: bytes, r: int, s: int):
    """
    椭圆曲线签名验证
    参数：
        e: 数据产生的哈希值
        r, s: 数字签名
    返回值：
        验证是否通过
    """
    if r < 1 or r > self.order - 1:
        return False
    if s < 1 or s > self.order - 1:
        return False
    t = (r + s) % self.order
    if t == 0:
        return False
    T = s * self.G + t * self.P
    R = (int.from_bytes(e, 'big') + int(T[0])) % self.order
    if R != r:
        return False
    return True

def raw_verify(self, M: bytes, ID: bytes, r: int, s: int):
    """
    椭圆曲线签名验证
    参数：
        M: 消息
        ID: 可辩别标识
        r, s: 数字签名
    返回值：
        验证是否通过
    """
    Z = self.ZHash(ID)
    e = sm3.hash(Z + M)
    return self.verify(e, r, s)

SM3

SM3 密码杂凑算法，即哈希算法。

SM3 适用于商用密码应用中的数字签名和验证，是在 SHA-256 基础上改进实现的一种算法，其安全性和 SHA-256 相当。SM3 和 MD5 的迭代过程类似，也采用 Merkle-Damgard 结构。消息分组长度为 512 位，摘要值长度为 256 位。

整个算法的执行过程可以概括成四个步骤：消息填充、消息扩展、迭代压缩、输出结果。

国密标准规范来源：https://www.sca.gov.cn/sca/xxgk/2010-12/17/content_1002389.shtml

常数与函数

初始值

1	IV = [0x7380166f, 0x4914b2b9, 0x172442d7, 0xda8a0600, 0xa96f30bc, 0x163138aa, 0xe38dee4d, 0xb0fb0e4e]

常量

1	T = [0x79cc4519] * 16 + [0x7a879d8a] * 48

布尔函数

def FF(X: int, Y: int, Z: int):
    """
    FFj 布尔函数，调用方式 FF[j](X, Y, Z)
    """
    ...
FF = [lambda X, Y, Z: X ^ Y ^ Z] * 16 + [lambda X, Y, Z: (X & Y) | (X & Z) | (Y & Z)] * 48

def GG(X: int, Y: int, Z: int):
    """
    GGj 布尔函数，调用方式 GG[j](X, Y, Z)
    """
    ...
GG = [lambda X, Y, Z: X ^ Y ^ Z] * 16 + [lambda X, Y, Z: (X & Y) | ((~X) & Z)] * 48

置换函数

ROTL = lambda X, P: ((X << P) | (X >> (32 - P))) & 0xFFFFFFFF
def P0(X: int):
    """
    置换函数 P0
    """    
    return X ^ ROTL(X, 9) ^ ROTL(X, 17)

def P1(X: int):
    """
    置换函数 P1
    """    
    return X ^ ROTL(X, 15) ^ ROTL(X, 23)

算法描述

消息填充

假设消息 \(m\) 的长度为 \(l\) 比特，将比特 1 添加到消息末尾，后填充比特 0 直到消息长度为 \(l' =448\pmod{512}\)，最后填充比特长度 \(l\) 的 64 位比特串到末尾。

def padding(msg: bytes):
    """
    消息填充
    参数：
        msg: 消息
    返回值：
        填充后的消息，长度为512的倍数
    """
    pad_length = (448 - len(msg) * 8) % 512 // 8 - 1
    return msg + b'\x80' + bytes(pad_length) + int(len(msg) * 8).to_bytes(8, 'big')

消息扩展

将 512 位的消息分组扩展为 132 字节的 \(W_0,W_1,\cdots,W_{67},W_0',\cdots,W_{63}'\)，用于压缩函数 \(CF\)。

def expand(Bi: bytes):
    """
    消息扩展
    参数：
        Bi: 64字节512位的消息块
    返回值：
        [W[0],...,W[67]],[W_[0],...,W_[63]]
    """
    W = [int.from_bytes(Bi[i:i+4], 'big') for i in range(0, len(Bi), 4)] + [0] * 52
    for j in range(16, 68):
        W[j] = P1(W[j - 16] ^ W[j - 9] ^ ROTL(W[j - 3], 15)) ^ ROTL(W[j - 13], 7) ^ W[j - 6]
    W_ = [0] * 64
    for j in range(0, 64):
        W_[j] = W[j] ^ W[j + 4]
    return W, W_

消息压缩

将消息分组 \(B_i\) 扩展后压缩为 16 字节的杂凑值

def CF(Vi: bytes, Bi: bytes):
    """
    消息压缩
    参数：
        Vi: 16字节64位的杂凑值
        Bi: 64字节512位的消息块
    返回值：
        Vi+1: 16字节64位的杂凑值
    """
    A, B, C, D, E, F, G, H = Vi
    W, W_ = expand(Bi)
    for j in range(64):
        SS1 = ROTL((ROTL(A, 12) + E + ROTL(T[j], j % 32)) & 0xFFFFFFFF, 7)
        SS2 = SS1 ^ ROTL(A, 12)
        TT1 = (FF[j](A, B, C) + D + SS2 + W_[j]) & 0xFFFFFFFF
        TT2 = (GG[j](E, F, G) + H + SS1 + W[j]) & 0xFFFFFFFF
        D = C
        C = ROTL(B, 9)
        B = A
        A = TT1
        H = G
        G = ROTL(F, 19)
        F = E
        E = P0(TT2)
    Vii = [A, B, C, D, E, F, G, H]
    return [(i ^ j) for i, j in zip(Vi, Vii)]

杂凑迭代

对填充过的消息分块后迭代压缩，最终杂凑值为 \(V_{i+1}\)。

def hash(msg: bytes):
    """
    哈希函数
    参数：
        msg: 消息
    返回值：
        32字节256比特的杂凑值（哈希值）
    """
    msg = padding(msg)
    hash_count = len(msg) // 64
    B = [msg[i:i+64] for i in range(0, len(msg), 64)]
    V = [IV] + [0] * hash_count
    for i in range(hash_count):
        V[i + 1] = CF(V[i], B[i])
    return b''.join(int(j).to_bytes(4, 'big') for j in V[i + 1])

基于 SM3 的 KDF

输入基密钥字节串 \(Z\) 和派生密钥字节长度 \(klen\)，输出派生密钥。

初始化 4 字节 32 比特计数器 ct=0x00000001
从 1 到 klen，计算 \(Ha=Ha||\mathrm{Hash}(Z||ct)\)

def KDF(Z: bytes, klen: int):
    """
    密钥派生算法（非标准实现，基于字节流实现）
    参数：
        Z: 基密钥字节串
        klen: 派生的密钥字节长度
    """
    assert klen < (2 ** 32 - 1) * 32
    ct = int(0x00000001)
    Ha = b''
    for _ in range(klen // 32 + 1):
        msg = Z + ct.to_bytes(4, 'big')
        Ha = Ha + hash(msg)
        ct += 1
    return Ha[0:klen]

SM4

SM4 分组密码算法，也是无线局域网标准的分组数据算法，是一种对称加密流密码，密钥长度和分组长度均为 128 比特 16 字节。

加密算法与密钥扩展算法都采用 32 轮非线性迭代结构，是典型的 Feistel 密码结构。

密钥及密钥参量

加密密钥长度 128 比特 16 字节，每组 32 比特 4 字节（标准 int32），共 4 组，表示为 \(MK=(MK_0,MK_1,MK_2,MK_3)\)。

轮密钥每组 32 比特 4 字节，共 32 组，表示为 \(rk=(rk_0,rk_1,\cdots,rk_{31})\)，轮密钥用于加密密钥生成。

\(FK=(FK_0,FK_1,FK_2,FK_3)\)，每组 32 比特 4 字节，共 4 组，为系统参数；

\(CK=(CK_0,CK_1,\cdots,CK_{31})\)，每组 32 比特 4 字节，共 32 组，为固定参数，二者都用于密钥扩展算法。

轮函数

轮函数结构

设输入为 128 比特 16 字节，每组 32 比特 4 字节，即 \((X_0,X_1,X_2,X_3)\)，轮密钥为 \(rk\)（32 组轮密钥中的一个），那么轮函数运算为 \[ F(X_0,X_1,X_2,X_3,rk)=X_0\oplus T(X_1\oplus X_2\oplus X_3\oplus rk) \]

合成置换

\(T\) 变换为可逆变换，由非线性变换 \(\tau\) 和线性变换 \(L\) 复合而成，即 \(T(X)=L(\tau(X))\)。

非线性变换 \(\tau\)

\(\tau\) 由四个并行的 S 盒构成。 \[ \tau(a_0,a_1,a_2,a_3)=(\mathrm{Sbox}(a_0),\mathrm{Sbox}(a_1),\mathrm{Sbox}(a_2),\mathrm{Sbox}(a_3)) \] 其中 \((a_0,a_1,a_2,a_3)\) 是每组 8 比特 1 字节的输入，且 \(\mathrm{Sbox}\) 的数据如下

Sbox = [
    0xd6, 0x90, 0xe9, 0xfe, 0xcc, 0xe1, 0x3d, 0xb7, 0x16, 0xb6, 0x14, 0xc2, 0x28, 0xfb, 0x2c, 0x05,
    0x2b, 0x67, 0x9a, 0x76, 0x2a, 0xbe, 0x04, 0xc3, 0xaa, 0x44, 0x13, 0x26, 0x49, 0x86, 0x06, 0x99,
    0x9c, 0x42, 0x50, 0xf4, 0x91, 0xef, 0x98, 0x7a, 0x33, 0x54, 0x0b, 0x43, 0xed, 0xcf, 0xac, 0x62,
    0xe4, 0xb3, 0x1c, 0xa9, 0xc9, 0x08, 0xe8, 0x95, 0x80, 0xdf, 0x94, 0xfa, 0x75, 0x8f, 0x3f, 0xa6,
    0x47, 0x07, 0xa7, 0xfc, 0xf3, 0x73, 0x17, 0xba, 0x83, 0x59, 0x3c, 0x19, 0xe6, 0x85, 0x4f, 0xa8,
    0x68, 0x6b, 0x81, 0xb2, 0x71, 0x64, 0xda, 0x8b, 0xf8, 0xeb, 0x0f, 0x4b, 0x70, 0x56, 0x9d, 0x35,
    0x1e, 0x24, 0x0e, 0x5e, 0x63, 0x58, 0xd1, 0xa2, 0x25, 0x22, 0x7c, 0x3b, 0x01, 0x21, 0x78, 0x87,
    0xd4, 0x00, 0x46, 0x57, 0x9f, 0xd3, 0x27, 0x52, 0x4c, 0x36, 0x02, 0xe7, 0xa0, 0xc4, 0xc8, 0x9e,
    0xea, 0xbf, 0x8a, 0xd2, 0x40, 0xc7, 0x38, 0xb5, 0xa3, 0xf7, 0xf2, 0xce, 0xf9, 0x61, 0x15, 0xa1,
    0xe0, 0xae, 0x5d, 0xa4, 0x9b, 0x34, 0x1a, 0x55, 0xad, 0x93, 0x32, 0x30, 0xf5, 0x8c, 0xb1, 0xe3,
    0x1d, 0xf6, 0xe2, 0x2e, 0x82, 0x66, 0xca, 0x60, 0xc0, 0x29, 0x23, 0xab, 0x0d, 0x53, 0x4e, 0x6f,
    0xd5, 0xdb, 0x37, 0x45, 0xde, 0xfd, 0x8e, 0x2f, 0x03, 0xff, 0x6a, 0x72, 0x6d, 0x6c, 0x5b, 0x51,
    0x8d, 0x1b, 0xaf, 0x92, 0xbb, 0xdd, 0xbc, 0x7f, 0x11, 0xd9, 0x5c, 0x41, 0x1f, 0x10, 0x5a, 0xd8,
    0x0a, 0xc1, 0x31, 0x88, 0xa5, 0xcd, 0x7b, 0xbd, 0x2d, 0x74, 0xd0, 0x12, 0xb8, 0xe5, 0xb4, 0xb0,
    0x89, 0x69, 0x97, 0x4a, 0x0c, 0x96, 0x77, 0x7e, 0x65, 0xb9, 0xf1, 0x09, 0xc5, 0x6e, 0xc6, 0x84,
    0x18, 0xf0, 0x7d, 0xec, 0x3a, 0xdc, 0x4d, 0x20, 0x79, 0xee, 0x5f, 0x3e, 0xd7, 0xcb, 0x39, 0x48
]

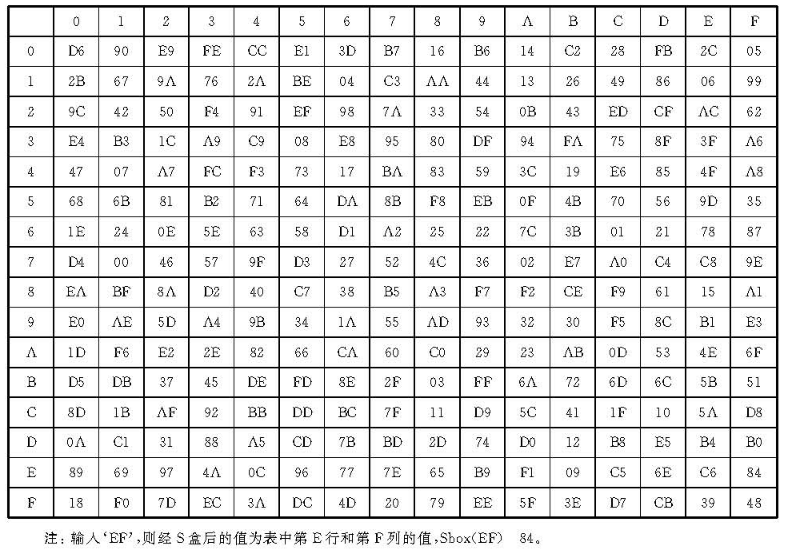
线性变换 \(L\)

非线性变换 \(\tau\) 的输出是线性变换 \(L\) 的输入。 \[ L(X)=X\oplus (X<<<2)\oplus(X<<<10)\oplus (X<<<18)\oplus(X<<<24) \] 其中 \(X\) 是 32 比特 4 字节的输入，\(<<<\) 代表循环左移。

加密

设明文输入为 \((X_0,X_1,X_2,X_3)\)，每组 32 比特 4 字节；

密文输出为 \((Y_0,Y_1,Y_2,Y_3)\)，每组 32 比特 4 字节；

轮密钥为 \(rk_i,i=0,1,\cdots,31\)。

运算过程如下：

32 次迭代运算：\(X_{i+4}=F(X_i,X_{i+1},X_{i+2},X_{i+3},rk_i),i=0,1,\cdots,31\)
反序变换：\((Y_0,Y_1,Y_2,Y_3)=(X_{35},X_{34},X_{33},X_{32})\)

解密

将轮密钥反序即可，即 \(rk'=(rk_{31},rk_{30},\cdots,rk_0)\)。

密钥扩展

轮密钥生成过程为

计算 \((K_0,K_1,K_2,K_3)=(MK_0\oplus FK_0,MK_1\oplus FK_1,MK_2\oplus FK_2,MK_3\oplus FK_3)\)
轮密钥 \(rk_i=K_{i+4}=K_i\oplus T'(K_{i+1}\oplus K_{i+2}\oplus K_{i+3}\oplus CK_i),i=0,1,\cdots,31\)

其中，\(T'\) 是将线性变换 \(L\) 变为 \(L'\)： \[ L'(X)=X\oplus (X<<<13)\oplus (X<<<23) \] 系统参数 \(FK\) 为

1	FK = [0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc]

固定参数 \(CK_i\) 为

CK = [
    0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
    0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
    0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
    0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
    0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
    0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
    0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
    0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279
]

SM9

SM9 是标识密码算法（Identity-base cryptogrphy），又称作身份基密码.

标准规范来源：http://www.gmbz.org.cn/main/bzlb.html

数字签名算法

标准推荐参数

使用 256 位的 BN 曲线，椭圆曲线方程为 \[ y^2=x^3+b \] 曲线参数为：

参数 \(t\)：0x600000000058F98A

迹 \(tr(t)=6t^2+1\)：0xD8000000019062ED0000B98B0CB27659

基域特征 \(q(t)=36t^4+36t^3+24t^3+6t+1\)：0xB640000002A3A6F1D603AB4FF58EC74521F2934B1A7AEEDBE56F9B27E351457D

方程参数 \(b\)：0x05

群的阶 \(N(t)=36t^4+36t^3+18t^2+6t+1\)：0xB640000002A3A6F1D603AB4FF58EC74449F2934B18EA8BEEE56EE19CD69ECF25

余因子 \(cf=1\)

嵌入次数 \(k=12\)

扭曲线的参数 \(\beta=\sqrt{-2}\)

\(k\) 的因子 \(d_1=1,d_2=2\)

曲线识别符 \(cid\)：0x12

群 \(G_1\) 的生成元 \(P_1\)：P1=(0x93DE051D62BF718FF5ED0704487D01D6E1E4086909DC3280E8C4E4817C66DDDD, 0x21FE8DDA4F21E607631065125C395BBC1C1C00CBFA6024350C464CD70A3EA616)

群 \(G_2\) 的生成元 \(P_2\)：

P2x=(0x85AEF3D078640C98597B6027B441A01FF1DD2C190F5E93C454806C11D8806141, 0x3722755292130B08D2AAB97FD34EC120EE265948D19C17ABF9B7213BAF82D65B)

P2y=(0x17509B092E845C1266BA0D262CBEE6ED0736A96FA347C8BD856DC76B84EBEB96, 0xA7CF28D519BE3DA65F3170153D278FF247EFBA98A71A08116215BBA5C999A7C7)

双线性对的识别符 \(eid\)：0x04

扩域相关：

二次扩张的约化多项式为 \(x^2+2\)

四次扩张的约化多项式为 \(x^2-\sqrt{-2}\)

十二次扩张的约化多项式为 \(x^3-(-2)^{1/6}\)

基于 Sagemath 的参数如下

t = 0x600000000058F98A
tr = 6 * t ** 2 + 1
q = 36 * t ** 4 + 36 * t ** 3 + 24 * t ** 2 + 6 * t + 1
b = 0x05
N = 36 * t ** 4 + 36 * t ** 3 + 18 * t ** 2 + 6 * t + 1
cf = 1
k = 12

Fq.<x> = GF(q)[]
E = EllipticCurve(Fqd1, [0, b])
Fq2.<u> = GF(p^2, modulus = x ^ 2 + 2)
# beta = sqrt(Fq2(-2))
beta = u
E2 = EllipticCurve(Fqd2, [0, b * beta])

P1x = 0x93DE051D62BF718FF5ED0704487D01D6E1E4086909DC3280E8C4E4817C66DDDD
P1y = 0x21FE8DDA4F21E607631065125C395BBC1C1C00CBFA6024350C464CD70A3EA616
P1 = E((P1x, P1y))

P2x = 0x85AEF3D078640C98597B6027B441A01FF1DD2C190F5E93C454806C11D8806141 * u + 0x3722755292130B08D2AAB97FD34EC120EE265948D19C17ABF9B7213BAF82D65B
P2y = 0x17509B092E845C1266BA0D262CBEE6ED0736A96FA347C8BD856DC76B84EBEB96 * u + 0xA7CF28D519BE3DA65F3170153D278FF247EFBA98A71A08116215BBA5C999A7C7
P2 = E2((P2x, P2y))

eid = 0x04

符号

加密主密钥

加密主密钥（encryption master key）处于标识密码密钥分层结构最顶层的密钥，内容为加密主私钥和加密主公钥，其中加密主公钥是公开的，而加密主私钥由密码生成中心（KGC）秘密保存。KGC 使用加密主私钥和用户的标识（ID）生成用户的加密私钥。

标识

标识（ID）由实体无法否认的信息组成，如电子邮箱、身份证号、电话号码等。

曲线识别符 cid

用于区分不同椭圆曲线的标识。

0x10 表示 \(F_p\) 上的常曲线，\(p\) 是素数，\(p>2^{191}\)
0x11 表示 \(F_p\) 上的超奇异曲线
0x12 表示 \(F_p\) 上的常曲线及其扭曲线

标准使用的是 BN 曲线（\(a=0,b=5\)），cid=0x12。

双线性对识别符 eid

0x01 表示 Tate 对
0x02 表示 Weil 对
0x03 表示 Ate 对
0x04 表示 R-ate 对

系统签名主密钥和用户签名密钥的产生

KGC 产生随机数 \(ks\in[1,N-1]\) 作为签名主私钥，计算群 \(G_2\) 中的元素 \(P_{pub-s}=ks\cdot P_2\) 作为签名主公钥，则签名主密钥对为 \((ks,P_{pub-s})\)。

KGC 秘密保存 \(ks\)，公开 \(P_{pub-s}\)。

KGC 选择并公开用一个字节表示签名私钥生成函数识别符 \(hid\)。

用户 A 的标识为 \(ID\)，KGC 在有限域 \(F_N\) 上计算 \(t_1=H_1(ID||hid,N)+ks\)，若 \(t_1=0\) 则重新计算签名主私钥、更新签名主密钥对；

随后计算 \(t_2=ks\cdot t^{-1}\pmod{N}\)；

最后计算签名私钥 \(ds=t_2\cdot P_1\)。

辅助函数

密码杂凑函数

标准推荐使用 SM3 密码杂凑算法，输出 256 比特 32 字节。

SM 系列算法

SM2

SM2公钥加密算法

符号

公钥与密钥

加密

解密

代码

SM2数字签名算法

符号

公钥与密钥

用户信息

签名

验证

代码

SM3

常数与函数

初始值

常量

布尔函数

置换函数

算法描述

消息填充

消息扩展

消息压缩

杂凑迭代

基于 SM3 的 KDF

SM4

密钥及密钥参量

轮函数

轮函数结构

合成置换

非线性变换 \(\tau\)

线性变换 \(L\)

加密

解密

密钥扩展

SM9

数字签名算法

标准推荐参数

符号

加密主密钥

标识

曲线识别符 cid

双线性对识别符 eid

系统签名主密钥和用户签名密钥的产生

辅助函数

密码杂凑函数

密码函数 \(H_1\)