模式识别-非参数技术笔记

发表于 更新于 本文字数： 6.7k 阅读时长 ≈ 6 分钟
有关非参数技术的简要笔记

非参数技术

K 最近邻算法

原理

K 最近邻算法（KNN）的原理很简单，我们考虑我们已知数据

橙子还是柚子？

这是我们现有的数据，假如说存在一个神秘的水果

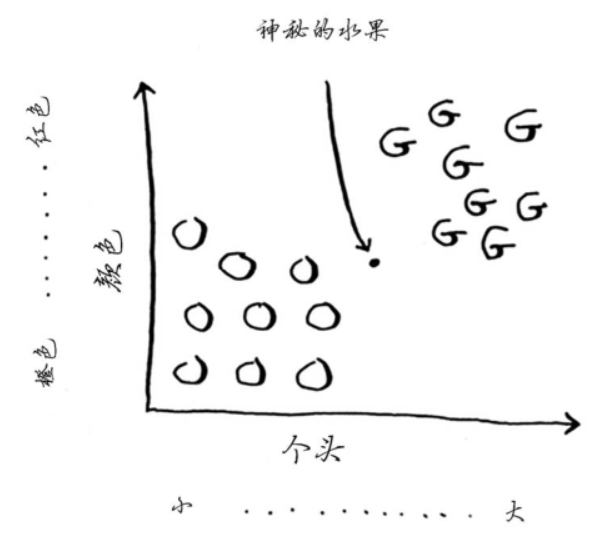
神秘的水果

我们判断它是橙子还是柚子的依据就是，来看谁是它最多的邻居。

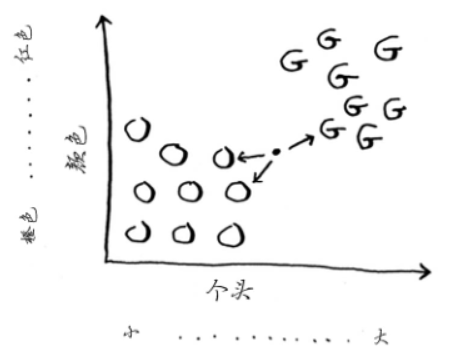
最多的邻居

我们可以计算得到，在三个邻居范围内，橙子比柚子多，所以，这个水果很有可能是橙子。

这就是 KNN 算法的基本原理，K 是其中的三。

距离度量

闵可夫斯基距离公式为 \[ L_p(\boldsymbol{x}_i,\boldsymbol{x}_j)=(\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^p)^{\frac{1}{p}} \] 如果 \(p=2\)，那么就是欧式距离 \[ L_2(\boldsymbol{x}_i,\boldsymbol{x}_j)=(\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^2)^{\frac{1}{2}} \] 如果 \(p=1\)，那么就是曼哈顿距离 \[ L_1(\boldsymbol{x}_i,\boldsymbol{x}_j)=\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}| \] 如果 \(p=\infin\)，那么就是切比雪夫距离 \[ L_\infin(\boldsymbol{x}_i,\boldsymbol{x}_j)=\max|x_i^{(l)}-x_j^{(l)}| \] 但是考虑到样本各个特征属性之间的尺度并不一定，相关性也不一定，特别是各个维度之间的分布（方差）不同，此时就需要使用马氏距离。

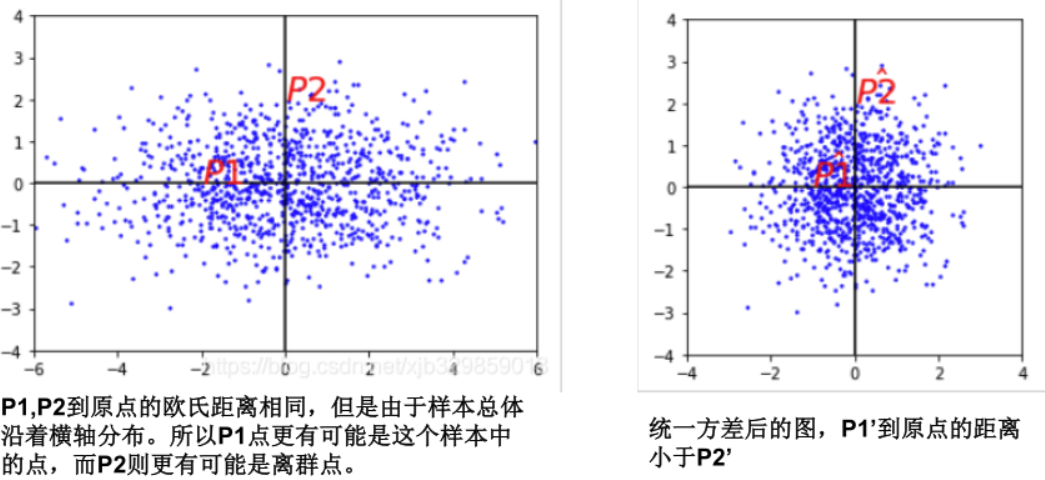
马氏距离解决问题

马氏距离公式为 \[ d_{Mahalanobis}=\sqrt{(\boldsymbol{x}-\boldsymbol{y})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{y})} \] 其中，\(\Sigma\) 是协方差矩阵。

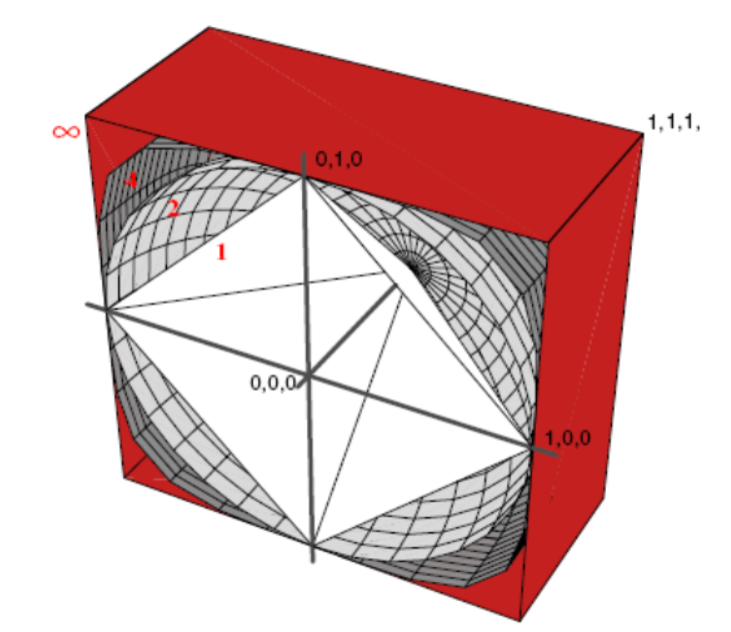
几种距离度量之间的关系

每一个彩色的平面由距离原点为 1 的点所形成。

代码

仅考虑两类样本，借助 numpy 计算闵可夫斯基距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import numpy as np

def distance(x: list, y: list):
    """
    计算闵可夫斯基距离
    """
    assert len(x) == len(y)
    p = len(x)
    return np.linalg.norm(np.array(x, np.float64) - np.array(y, np.float64), ord = p)

def KNN(omega1: list[list], omega2: list[list], x: list, K: int):
    """
    参数：
        omega1: 第一类样本，一个二维矩阵，行是单个样本
        omega2: 第二类样本，一个二维矩阵，行是单个样本
        x: 待分类样本
        K: k近邻
    """
    dis = []
    # 计算所有待分类样本与已知样本的距离
    for o1 in omega1:
        dis.append((distance(x, o1), "o1"))
    for o2 in omega2:
        dis.append((distance(x, o2), "o2"))
    # 按距离排序，取K个邻居
    kdis = sorted(dis, key = lambda x: x[0])[:K]
    # 获取这K个邻居的类别
    komega = [d[1] for d in kdis]
    # 计算K个邻居中为omega1的个数
    nn = komega.count("o1")
    # K-nn即omega2的个数
    if nn > K - nn:
        return "omega1"
    else:
        return "omega2"

omega1 = [
    [1, 0], [0, 1], [0, -1]
]
omega2 = [
    [0, 0], [0, 2], [0, -2], [-2, 0]
]
x = [1, 2]
KNN(omega1, omega2, x, 3)

优缺点

如果 K 推向正无穷，那么就会利用全部的训练样本做训练，哪一类样本多就属于哪一类，会导致欠拟合，训练误差加大。

如果 K 值小，则模型复杂度较高，容易发生过拟合，而且预测结果对近邻实例点非常敏感，容易被噪声（noise）影响。

在应用中，通常采用交叉验证法来选取最优的 K 值，一般取奇数（保证不会出现两类邻居数量相等）。

KNN 不对样本做任何假设和分布估计，是一种懒惰算法，常用于作为一个基准分类器，比较容易解决多雷问题，且足够多训练数据下，KNN 可以实现任意分布数据的贝叶斯误差收敛（泛一致性）。

简言之，足够多训练数据下，KNN 分类器收敛到贝叶斯分类器（误差收敛）。

缺点是计算空间大，需要存储全部训练样本的信息，且计算开销大，需要计算测试样本与每一个训练样本的距离，同时同样容易陷入维数灾难，较少的训练样本性能一般也不太好。

主成分分析

简介

主成分分析（Principal Component Analysis, PCA）是统计学上常用的方法，通常是为了找出数据中最主要的元素和结构，去除噪音和冗余，将原有的复杂数据降维，揭示隐藏在复杂数据背后的简单结构。

PCA 的功能是简化复杂数据到低维空间，从而发现数据中隐藏的简单结构。

其简单且无参数限制，被誉为应用线性代数最价值的结果之一。

PCA 的目标是去除冗余，并发现重要特征。

不同于 LDA（最小化类内散度和最大化类间距离），它是单纯的降维。

方差

一般来说，方差是对于全体而言的，即 \[ \sigma^2=\frac{1}{n}\sum_{i=1}^n(x_i-\mu)^2 \] 其中，\(\mu\) 是全体均值，\(n\) 是全体数量。

但是考虑到，如果要计算所有的数据，负担太大，所以我们一般采用随机采样，然后计算这部分样本的方差，即样本方差 \[ s^2=\frac{1}{n-1}\sum^n_{i=1}(x_i-\mu)^2 \] 其中，\(n-1\) 是贝塞尔矫正，为了平衡自由度降低导致计算得到的样本方差减低。

但对于多维数据，我们并不能直接使用方差公式，此时需要改为用协方差 \[ Cov(\boldsymbol{x},\boldsymbol{y})=\frac{1}{n-1}\sum^n_{i=1}(x_i-\bar{x})(y_i-\bar{y}) \] 协方差矩阵用于描述多维度之间的相关性。

协方差绝对值越大，其相关关系越明显。

而方差的大小决定了数据在某一方向上的分散程度。

考虑一组数据

房价（百万元） 面积（百平米）
10 10
2 2
1 1
7 7
3 3

那么我们可以写出代码

1
2
3
4
5
6
7
8
9
10
11
import numpy as np

data = [
    [10, 2, 1, 7, 3],
    [10, 2, 1, 7, 3]
]
np.cov(data)
"""
array([[14.3, 14.3],
       [14.3, 14.3]])
"""

可以发现，两类样本之间相关程度大，且在 \(x\) 和 \(y\) 方向分散程度一致。

基变换

考虑原坐标系为直角坐标系，则其的基（basis）为 \[ \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} \] 考虑我们想将坐标 \((3,2)\) 转换到新正交基坐标系 \[ \begin{bmatrix} 1/\sqrt{2}&1/\sqrt{2}\\ -1/\sqrt{2}&1/\sqrt{2} \end{bmatrix} \] 那么仅需计算 \[ \begin{bmatrix} 1/\sqrt{2}&1/\sqrt{2}\\ -1/\sqrt{2}&1/\sqrt{2} \end{bmatrix}\begin{pmatrix} 3\\ 2 \end{pmatrix}=\begin{pmatrix} 5/\sqrt{2}\\ -1/\sqrt{2} \end{pmatrix} \] 同样的如果对三个点 \((1,1),(2,2),(3,3)\) 变换到新坐标系下，则计算 \[ \begin{bmatrix} 1/\sqrt{2}&1/\sqrt{2}\\ -1/\sqrt{2}&1/\sqrt{2} \end{bmatrix}\begin{pmatrix} 1&2&3\\ 1&2&3 \end{pmatrix}=\begin{pmatrix} 2/\sqrt{2}&4/\sqrt{2}&6/\sqrt{2}\\ 0&0&0 \end{pmatrix} \] 因此，基变换（坐标变换）可以被表示为矩阵相乘，使用矩阵对向量空间进行旋转（向量旋转）。

PCA 算法

基本数学工具是矩阵对角化。

考虑房价与面积的数据，我们对矩阵进行矩阵对角化，得到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np

data = [
    [10, 2, 1, 7, 3],
    [10, 2, 1, 7, 3]
]
C = np.cov(data)
eig_val, eig_vec = np.linalg.eig(C)
eigC = np.diagflat(eig_val)
eigC
"""
array([[28.6,  0. ],
       [ 0. ,  0. ]])
"""

可以发现，矩阵对角化后显然仅有第一列数据是有意义的，而第二列数据的方差为 0，其是无意义的。

算法步骤如下：

  1. 将原始数据按列组成 \(n\times m\) 矩阵 \(X\)
  2. 将 \(X\) 的每一行进行去中心化（零均值化），即减去这一行的均值
  3. 求出协方差矩阵 \(C=\frac{1}{m}XX^T\)（除以 \(m-1\) 或者忽略都可以）
  4. 求出协方差矩阵的特征值和特征向量
  5. 将特征向量按特征值大小从上到下按行排列成矩阵，取前 \(k\) 行组成矩阵 \(P\)，即将矩阵从 \(n\) 维降低到 \(k\) 维。
  6. \(Y=PX\) 即为降维到 \(k\) 维后的数据。

示例

考虑 5 个二维样本 \[ X=\begin{bmatrix} -1&-1&0&2&0\\ -2&0&0&1&1 \end{bmatrix} \] 去中心化（样本本身已经中心化了）。

求协方差矩阵 \[ C=\frac{1}{5}\begin{bmatrix} -1&-1&0&2&0\\ -2&0&0&1&1 \end{bmatrix}\begin{bmatrix} -1&-2\\ -1&0\\ 0&0\\ 2&1\\ 0&1 \end{bmatrix}=\begin{bmatrix} 1.2&0.8\\ 0.8&1.2 \end{bmatrix} \] 求特征值及特征向量 \[ \lambda_1=2,\lambda_2=0.4\\ c_1=(1,1)^T,c_2=(-1,1)^T \] 那么可以得到标准化正交基（标准化需要向量长度为 1）为 \[ P=\begin{bmatrix} 1/\sqrt{2}&1/\sqrt{2}\\ -1/\sqrt{2}&1/\sqrt{2} \end{bmatrix} \] 只选取特征值最大投影方向进行降维，那么 \[ Y=\begin{pmatrix} -3/\sqrt{2}&-1/\sqrt{2}&0&3/\sqrt{2}&-1/\sqrt{2} \end{pmatrix} \]

这里是计算 \(Y'=PX\)，随后仅取第一行，因为第一行的特征值为 2，是最大值。

使用 numpy 可以写出代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np

X = [
    [-1, -1, 0, 2, 0],
    [-2, 0, 0, 1, 1]
]
C = np.cov(X)
eig_val, eig_vec = np.linalg.eig(C)
print(eig_val)
Y = eig_vec @ X
Y = Y[0]
print(Y)
"""
[2.5 0.5]
[ 0.70710678 -0.70710678  0.          0.70710678 -0.70710678]
"""

聚类

原理

聚类目标：将数据集中的样本划分为若干个通常不相交的子集。

聚类既可以作为一个单独过程（用于找寻数据内在的分布结构），也可作为分类等其他学习任务的前驱过程。

K 均值算法

K 均值算法又称 K-means 算法，K 是聚类算法中类的个数，means 是均值算法，故算法本身是采用均值算法把数据分成 K 类的算法。

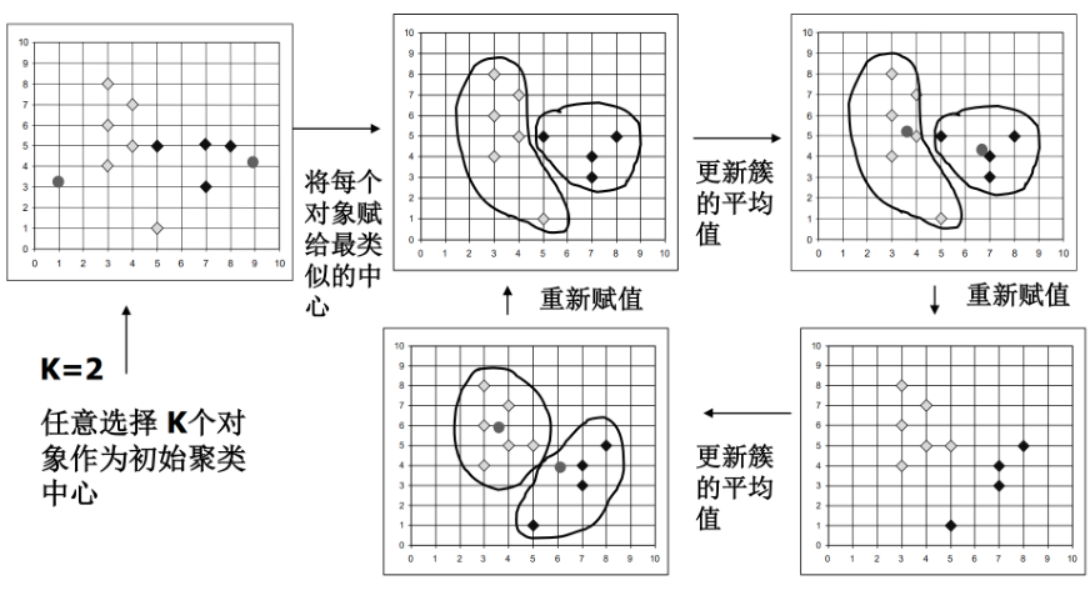
K均值算法流程

在聚类任务中，我们通常定义一个聚类准则函数来评价聚类结果的质量，可以类比线性分类中的损失函数。

如果聚类质量不满足要求，就要重复执行聚类过程，以优化结果。

最常用的是误差平方和准则 \[ J_c=\sum^c_{j=1}\sum^{n_j}_{k=1}\|x_k-m_j\|^2 \] 其中 \(m_j=\frac{1}{n_j}\sum^{n_j}_{j=1}x_j\)，是该集合的中心，用来代表 K 个类型。

而 \(J_c\) 是样本和集合中心的函数，在样本集 \(X\) 给定的情况下，\(J_c\) 的取值取决于 \(c\) 个集合中心。

试验样本聚合成 \(c\) 个类型时，所产生的总误差平方和 \(J_c\) 越小越好。

考虑以下西瓜数据集，来运行 K 均值算法。

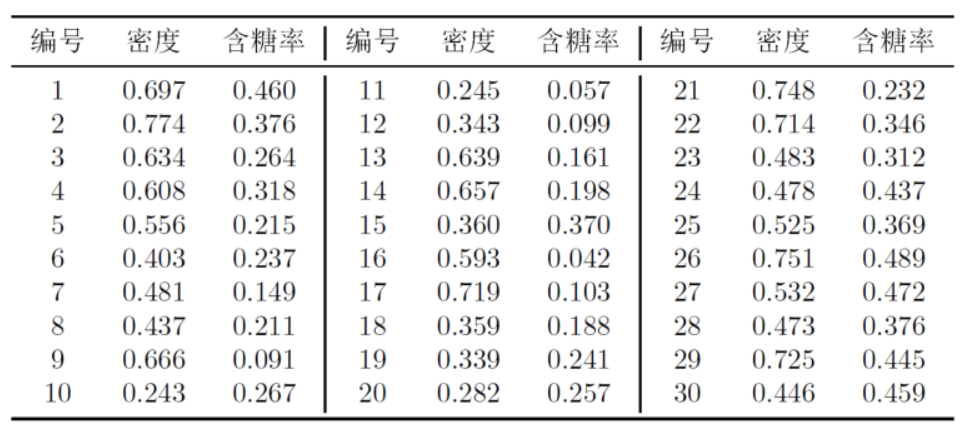
西瓜数据集 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import numpy as np
import random
from matplotlib import pyplot as plt

def distance(x: list, y: list):
    """
    计算闵可夫斯基距离
    """
    p = len(x)
    return np.linalg.norm(np.array(x, np.float64) - np.array(y, np.float64), ord = p)

def Kmeans(X: list[tuple[int, int]], K: int, round: int = 1):
    mu = random.choices(X, k = K)
    colors = random.choices('bgrcmyk', k = K)
    # mu = [X[5], X[11], X[26]]

    for i in range(round):
        omegas = [[] for _ in range(K)]
        for x in X:
            dis = [distance(x, m) for m in mu]
            idx = np.argmin(dis)
            omegas[idx].append(x)
        mu = [np.mean(omega, axis=0, dtype = np.float64) for omega in omegas]
        plt.subplot(round, 1, i + 1)
        for c, omega in zip(colors, omegas):
            plt.scatter([p[0] for p in omega], [p[1] for p in omega], c = c, s = 20)
    return omegas
X = [
    (0.697, 0.46), (0.774, 0.376), (0.634, 0.264), (0.608, 0.318), (0.556, 0.215),
    (0.403, 0.237), (0.481, 0.149), (0.437, 0.211), (0.666, 0.091), (0.243, 0.267),
    (0.245, 0.057), (0.343, 0.099), (0.639, 0.161), (0.657, 0.198), (0.36, 0.37),
    (0.593, 0.042), (0.719, 0.103), (0.359, 0.188), (0.339, 0.241), (0.282, 0.257),
    (0.748, 0.232), (0.714, 0.346), (0.483, 0.312), (0.478, 0.437), (0.525, 0.369),
    (0.751, 0.489), (0.532, 0.472), (0.473, 0.376), (0.725, 0.445), (0.446, 0.459)
]
Kmeans(X, 3, round = 5)