z变换与z域分析
\(z\) 变换与 \(z\) 域分析
幂级数
定义
标准幂级数是指形如 \[ \sum^{\infin}_{i=0}a_ix_i \] 的一系列级数。
收敛
等比级数 \[ \sum^\infin_{i=0}x^n \] 在 \((-1,1)\) 内收敛,有和函数 \[ \sum^\infin_{i=0}x^n=\frac{1}{1-x} \]
\(z\) 变换
定义
\(z\) 变换的定义是基于拉氏变换推导的,其中定义 \(z=e^{s}\),是一个复变量。
与拉氏变换相似,\(z\) 变换也有单边和双边之分。
对于序列 \(x(n)\) 的单边 \(z\) 变换定义为 \[ X(z)=\mathscr{Z}[x(n)]=\sum^\infin_{n=0}x(n)z^{-n} \]
在复变函数里,这是一个洛朗级数。
而对于双边序列 \(x(n)\),可以定义双边 \(z\) 变换为 \[ X(z)=\mathscr{Z}[x(n)]=\sum^{\infin}_{-\infin}x(n)z^{-n} \] 如果 \(x(n)\) 是因果序列,则双边变换与单边变换是等价的。
典型序列的 \(z\) 变换
单位样值函数
\[ \delta(n)\to \sum^{\infin}_{n=0}\delta(n)z^{-n}=1 \]
可见类似单位冲激函数的拉氏变换。
单位阶跃序列
\[ u(n)\to \sum^\infin_{n=0}u(n)z^{-n}=\sum^\infin_{n=0}z^{-n} \]
这是一个典型洛朗幂级数,可以知道这个级数在 \(|z|>1\) 时收敛,收敛为 \[ u(n)\to \frac{1}{1-z^{-1}}=\frac{z}{z-1} \]
斜变序列
\[ nu(n)=\sum^\infin_{n=0}nz^{-n} \]
考虑对收敛半径为 \(|z|>1\) 的洛朗级数求导 \[ \sum^\infin_{n=0}z^{-n}=\frac{1}{1-z^{-1}}\\ \sum^\infin_{n=0}n(z^{-1})^{n-1}=\frac{1}{(1-z^{-1})^2} \] 两边同乘 \(z^{-1}\) 即得到斜变序列的 \(z\) 变换 \[ nu(n)\to \sum^\infin_{n=0}nz^{-n}=\frac{z}{(z-1)^2} \] 该级数的收敛于也是 \(|z|>1\)。
再往下推导,可以知道 \[ n^2u(n)\to \frac{z(z+1)}{(z-1)^3}\\ n^3u(n)\to \frac{z(z^2+4z+1)}{(z-1)^3}\\ \cdots \]
指数序列
\[ x(n)\to \sum^\infin_{n=0}a^nz^{-n} \]
显然对于该洛朗级数,收敛半径为 \(|z|>|a|\),收敛结果为 \[ x(n)\to \frac{z}{z-a} \]
对两边求导也可以得到 \[ na^nu(n)\to \frac{az}{(z-a)^2}\\ n^2a^nu(n)\to \frac{az(z+a)}{(z-a)^3}\\ \cdots \]
正弦与余弦序列
由指数序列的 \(z\) 变换可得 \[ e^{bn}u(n)\to\frac{z}{z-e^b} \] 该级数的收敛半径为 \(|z|>|e^b|\)。
那么就有 \[ e^{\mathrm{j}\omega_0n}u(n)\to \frac{z}{z-e^{\mathrm{j}\omega_0}}\\ e^{-\mathrm{j}\omega_0n}u(n)\to \frac{z}{z-e^{-\mathrm{j}\omega_0}} \] 两式相加相减即可得到正、余弦序列的 \(z\) 变换 \[ \cos{(\omega_0n)}u(n)\to\frac{1}{2}(\frac{z}{z-e^{\mathrm{j}\omega_0}}+\frac{z}{z-e^{-\mathrm{j}\omega_0}})\\ \sin{(\omega_0n)}u(n)\to\frac{1}{2\mathrm{j}}(\frac{z}{z-e^{\mathrm{j}\omega_0}}-\frac{z}{z-e^{-\mathrm{j}\omega_0}}) \] 即 \[ \cos{(\omega_0n)}u(n)\to\frac{z(z-\cos\omega_0)}{z^2-2z\cos\omega_0+1}\\ \sin{(\omega_0n)}u(n)\to\frac{z\sin\omega_0}{z^2-2z\cos\omega_0+1} \] 这两个级数的收敛半径都为 \(|z|>1\)。
\(z\) 变换收敛域
首先需要明确,只有级数收敛的时候 \(z\) 变换才有意义。
级数收敛的充分条件
在复变函数中,级数收敛必须满足 \[ \sum^\infin_{-\infin}|x(n)z^{-n}|<\infin \] 一般转化为证明 \[ \lim_{n\to\infin}S(n)<\infin \] 即该级数的前 \(n\) 项和在 \(n\) 趋近于 \(\infin\) 时是有极限的。
级数收敛的必要条件
\[ \lim_{n\to \infin}|x(n)z^{-n}|=0 \]
即级数的通项在 \(n\) 趋近于 \(\infin\) 时是趋于零的。
级数审敛法
比值审敛法
对于正向级数 \(\sum|a_n|\),如果后项与前项比值的极限等于 \(\rho\) \[ \lim_{n\to\infin}\left|\frac{a_{n+1}}{a_n}\right|=\rho \] 如果 \(\rho<1\),那么级数收敛;
如果 \(\rho>1\),那么级数发散;
如果 \(\rho=1\),那么级数可能收敛可能发散。
根值审敛法
对于正向级数 \(\sum|a_n|\),如果通项开 \(n\) 次根号的极限等于 \(\rho\) \[ \lim_{n\to\infin}\sqrt[n]{a_n}=\rho \] 如果 \(\rho<1\),那么级数收敛;
如果 \(\rho>1\),那么级数发散;
如果 \(\rho=1\),那么级数可能收敛可能发散。
收敛域
\(z\) 变换的结果实际上是一个洛朗级数,可以分为两边 \[ \sum^\infin_{-\infin}x(n)z^{-n}=\sum^{-1}_{n=-\infin}x(n)z^{-n}+\sum^\infin_{n=0}x(n)z^{-n} \] 左半边级数(\(z^1+z^2+\cdots\))的收敛域为 \(|z|<R_2\);
右半边级数(\(z^0+z^{-1}+\cdots\))的收敛域为 \(|z|>R_1\);
重叠部分就是双边级数的收敛域 \(R_1<|z|<R_2\)。
在审敛法的基础上,
对于左半边级数,收敛域应该为 \(|z|<\frac{1}{\rho}\);
对于右半边级数,收敛域应该为 \(|z|>\frac{1}{\rho}\)。
逆 \(z\) 变换
定义
\[ x(n)=\mathscr{Z}^{-1}[X(z)]=\frac{1}{2\pi\mathrm{j}}\oint_CX(z)z^{n-1}\mathrm{d}z \]
这是一个复积分。
围线积分法(留数法)
即使用复变函数中的留数定理 \[ x(n)=\frac{1}{2\pi\mathrm{j}}\oint_CX(z)z^{n-1}\mathrm{d}z =\sum^m_{i=1}Res[X(z)z^{n-1},p_i] \] 留数公式为 \[ Res[X(z)z^{n-1},p_i]=\frac{1}{(p_i-1)!}\lim_{z\to p_i}\frac{\mathrm{d}^{p_i-1}}{\mathrm{d}z^{p_i-1}}[(z-p_i)X(z)z^{n-1}] \] 例如求以下复序列的逆变换 \[ X(z)=\frac{z^2}{(z-1)(z-0.5)},|z|>1 \] 首先记作新序列 \[ T(z)=X(z)z^{n-1}=\frac{z^{n+1}}{(z-1)(z-0.5)},|z|>1 \] 当 \(n\geq -1\) 时,可以知道该复序列有两个极点 \(p_1=1,p_2=0.5\),那么求该极点留数 \[ Res[T(z),1]=\lim_{z\to 1}\frac{z^{n+1}}{z-0.5}=2\\ Res[T(z),0.5]=\lim_{z\to 0.5}\frac{z^{n+1}}{z-1}=-(0.5)^n \] 那么可以写出 \[ x(n)=[2-(0.5)^n]u(n+1) \] 当 \(n<-1\) 时,可以知道该复序列新增 \(n+1\) 阶极点 \(p_3=0\),计算得到最终结果为 \(x(n)=0\)。
由于 \(x(-1)=0\),故可以写成 \[ x(n)=[2-(0.5)^n]u(n) \]
幂级数展开法(长除法)
考虑把 \(z\) 变换看作是幂级数,那么 \(x(n)\) 就是幂级数的系数。

部分分式展开法
\(z\) 变化的基本形式是 \(\frac{z}{z-z_m}\),考虑展开 \(\frac{X(z)}{z}\),然后每个分式乘以 \(z\),那么对于一阶极点可以展开成基本形式。
考虑使用部分分式展开法求解逆变换。 \[ X(z)=\frac{z^2}{z^2-1.5z+0.5},|z|>1 \] 可以变形为 \[ X(z)=\frac{z^2}{(z-1)(z-0.5)} \] 只包含一阶极点 \(z_1=0.5,z_2=1\),考虑展开为 \[ \frac{X(z)}{z}=\frac{A_1}{z-0.5}+\frac{A_2}{z-1} \] 使用(拉普拉斯变换中的)留数法可得 \[ A_1=\lim_{z\to1}\frac{z}{z-0.5}=2\\ A_2=\lim_{z\to0.5}\frac{z}{z-1}=-1 \] 那么有 \[ X(z)=\frac{2z}{z-1}-\frac{z}{z-0.5} \] 那么可以得到 \[ x(n)=(2-0.5^n)u(n) \] 更一般地,\(X(z)\) 表达式为 \[ X(z)=\frac{N(z)}{D(z)}=\frac{\sum^r_{j=0}b_jz^j}{\sum^k_{i=0}a_iz^i} \] 与拉普拉斯变换中的部分分式展开法一致,不再赘述。
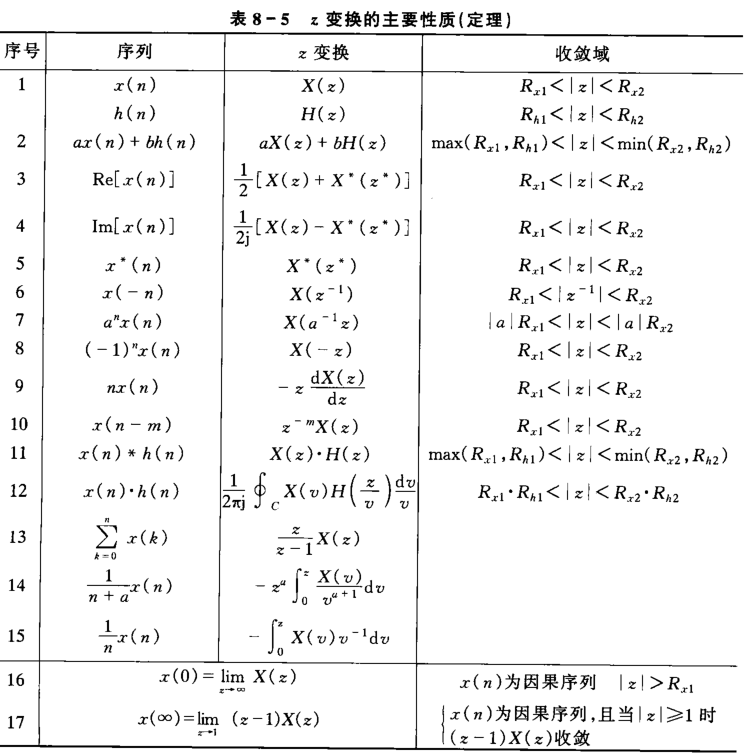
基本性质
线性
\[ ax(n)+by(n)\to aX(z)+bY(z) \]
位移性
对于双边 \(z\) 变换 \[ x(n-m)\to z^{-m}X(z) \] 对于单边 \(z\) 变换,要将多余的部分减掉 \[ x(n+m)\to z^m[X(z)-\sum^{m-1}_{k=0}x(k)z^{-k}] \]
序列线性加权(\(z\) 域微分)
\[ nx(n)\to -z\frac{\mathrm{d}}{\mathrm{d}z}X(z) \]
如果是连续微分,那么 \[ n^2x(n)\to-z\frac{\mathrm{d}}{\mathrm{d}z}[-z\frac{\mathrm{d}}{\mathrm{d}z}X(z)] \]
序列指数加权(\(z\) 域尺度变换)
\[ a^nx(n)\to X(\frac{z}{a}) \]
初值定理
\[ x(0)=\lim_{z\to \infin}X(z) \]
终值定理
\[ \lim_{z\to \infin}x(n)=\lim_{z\to 1}[(z-1)X(z)] \]
时域卷积
\[ x(n)*h(n)=X(z)H(z) \]
主要性质
\(z\) 变换与拉氏变换的关系
指数函数 \(e^{-at}u(t)\)
的拉氏变换为 \[
\frac{1}{s+a}
\] 对其进行 \(z\) 变换,得到
\[
X(z)=\frac{1}{1-z^{-1}e^{-aT}}=\frac{z}{z-e^{-aT}}
\] 特别地,对于阶跃信号即 \(a=0\) 时的特殊情况,有 \[
F(s)=\frac{1}{s+1}\newline
X(z)=\frac{z}{z-1}
\] 而对于正弦信号 \(\sin{(\omega_0t)}u(t)\) 的拉氏变换为 \[
\frac{\omega_0}{s^2+\omega_0^2}
\] 可以求得 \(z\) 变换为 \[
X(z)=\frac{z\sin{(\omega_0T)}}{z^2-2z\cos{(\omega_0T)}+1}
\] 