离散时间系统
离散时间系统
高中数学——数列
基本概念
在高中数学中,曾学过概念数列,数列是一组序列,即有序数的列表,例如 \[ \{x_0,x_1,\cdots,x_n\} \] 其中有无穷数列、有穷数列的区分,又有周期数列、非周期序列的区分。
如果一个数列可以用表达式描述,那么记作 \[ a_n=f(n) \] 其中,\(n\in\Zeta\)。
而在高中阶段,研究的最多的是等差数列和等比数列。
等差数列
考虑一个数列,其前一个值与后一个值的差值是恒定的,记作 \[ a_{n+1}-a_n=d \] 其中,\(d\) 是恒定常数。
那么我们把这样一个组合的数列称作是等差数列,这样的一个数列为 \[ \{a_0,a_0+d,\cdots,a_0+nd\} \] 很自然,我们可以使用一个表达式描述它,即 \[ a_n=a_0+nd \] \(a_0\) 是数列首项元素,\(d\) 是数列公差。
等差数列的求和也是容易的,我们记 \(S_n\) 为一个数列的前 \(n\) 项元素和,对等差数列而言,有 \[ S_n=a_0+a_1+\cdots+a_n=\frac{(a_0+a_n)n}{2} \] 描述为,等差数列的前 \(n\) 项和为首项加末项的和,乘以 \(n\) 除以 \(2\)。
等比数列
考虑一个数列,其前一个值与后一个值的比值是恒定的,记作 \[ \frac{a_{n+1}}{a_n}=q \] 其中,\(q\) 是恒定常数。
那么我们把这样一个组合的数列称作是等差数列,这样的一个数列为 \[ \{a_0,a_0q,\cdots,a_0q^{n-1}\} \] 很自然,我们可以使用一个表达式描述它,即 \[ a_n=a_0q^{n-1} \] \(a_0\) 是数列首项元素,\(q\) 是数列公比。
等比数列的求和也是容易的,我们记 \(S_n\) 为一个数列的前 \(n\) 项元素和,对等比数列而言,有 \[ S_n=a_0+a_1+\cdots+a_n=\frac{a_1(1-q^n)}{(1-q)} \] 这里需要注意的是,公比 \(q>1\) 才成立,如果公比 \(q=1\),这也是一个等比数列,但此时其前 \(n\) 项和为 \(S_n=na_0\)。
离散时间信号
序列
离散时间信号可以看作是连续时间信号的采样结果,它是时间上不连续的序列,通常给出函数值的离散时刻间隔是均匀的。如果该时间间隔为 \(T\),那么定义以 \(x(nT)\) 描述该离散时间信号,一般为方便描述会取 \(nT\) 为整数,那么可以简写为 \[ x(n)=\{\cdots,x_{-1},x_0,x_1,\cdots\} \] 这与高中的数列知识类似的,只是扩展了负整数域。
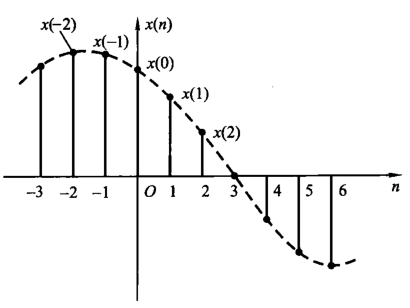
其中,虚线是沿着序列值描绘的一条曲线,一般称作是离散时间信号的包络线。
性质
与连续时间信号一样的,离散时间信号也有一些基本的性质。
线性性
\[ z(n)=x(n)+y(n) \]
可以看作是两个序列对应值相加,最终得到新序列。 \[ z(n)=x(n)y(n) \] 数学上的理解,可以将 \(x(n),y(n)\) 描述成一个多项式,然后对它们进行多项式乘法,得到的新的多项式就是新序列。
平移性
\[ z(n)=x(n-m) \]
这表示了让 \(x(n)\) 序列向右平移(后移) \(m\) 个单位,其中 \(m\in\Zeta\)。
同样的,向左移动(前移)\(m\) 个单位为 \[ z(n)=x(n+m) \]
左加右减。
反褶
\[ z(n)=x(-n) \]
这表示将序列图像沿着 \(y\) 轴做对称。
尺度变化
\[ z(n)=x(an) \]
\(a\) 必须是一个整数,这代表将 \(x(n)\) 压缩,这会使得某些点(序列值)去除。
同样的,我们也可以将 \(x(n)\) 扩展,即 \[ z(n)=x(\frac{n}{a}) \] 这会使得某些点(序列值)补 \(0\)。
因此,这种运算也称作是序列的重排。
例如序列 \(x(n)\) 为阶梯序列,即 \[ x(n)=\{0,1,2,\cdots,n\} \] 那么对其进行尺度变化 \(x(2n),x(\frac{n}{2})\)。

经典序列
单位样值信号
单位样值信号(unit sample / unit impulse),即单位取样、单位脉冲、单位冲激。 \[ \delta(n)=\begin{cases} 1&(n=0)\\ 0&(n\neq 0) \end{cases} \] 即强定义 \(\delta(0)=1\),其余点均为 \(0\)。
单位阶跃序列
\[ u(n)=\begin{cases} 1&(n\geq 0)\\ 0&(n<0) \end{cases} \]
其中需要注意的是,连续时间信号中 \(u(0)\) 处一般不定义或定义为 \(\frac{1}{2}\),但在离散时间信号中,强定义为 \(u(0)=1\)。
矩形序列
\[ R_N(n)=\begin{cases} n&(0\leq n\leq N-1)\\ 0&(n<0,n\geq N) \end{cases} \]
即从 \(n=0\) 开始,到 \(n=N-1\) 处,共有 \(N\) 个幅度为 \(1\) 的数值,其余点皆为零,即共有 \(N\) 个为 \(1\) 的序列点。
同样的可以用单位阶跃序列描述,即 \[ R_N(n)=u(n)-u(n-N) \]
斜变序列
\[ x(n)=nu(n) \]
即序列 \[ \{\cdots,0,0,1,2,\cdots\} \] 它的包络线是斜变函数 \(f(t)=t\)。
指数序列
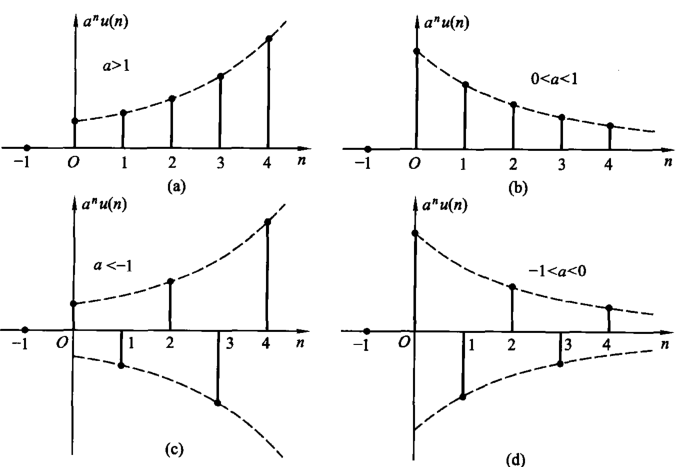
\[ x(n)=a^nu(n) \]
需要注意的是,如果 \(a<0\),那么将会出现正负跳变的序列图像。
正弦序列
\[ x(n)=\sin{(n\omega_0)} \]
其中,\(\omega_0\) 是正弦序列的频率,它反映序列值周期性重复的速率。
当 \(T=\frac{2\pi}{\omega_0}\) 为整数时,代表正弦序列值每 \(T\) 个后就重复;当 \(T\) 为有理数时,写成 \(T=\frac{p}{q}\) 形式,代表代表正弦序列值每 \(pq\) 个后就重复。这两种情况称正弦序列 \(x(n)\) 具有周期性。
无论正弦序列是否具有周期性,都固有称 \(\omega_0\) 为它的频率。
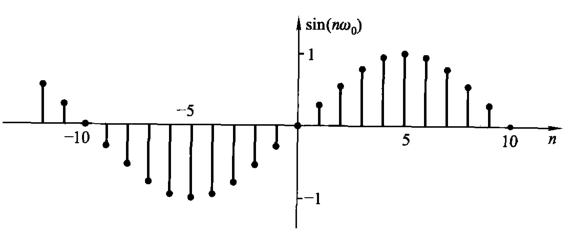
而正弦序列的得来是从正弦波中抽样,考虑连续信号为 \[ f(t)=\sin{(\Omega_0t)} \] 那么抽样值写作 \[ x(n)=f(nT)=\sin{(n\Omega_0T)} \] 此时我们称,\(T\) 是抽样间隔时间,\(f_s=\frac{1}{T}\) 是抽样频率,\(\omega_0=\frac{\Omega_0}{f_s}\) 是正弦序列的频率。
与正弦序列相对应的还有余弦序列 \[ x(n)=\cos{n\omega_0} \]
复指数序列
序列也可以取复数值,称为复序列。
复指数序列定义为 \[ x(n)=e^{\mathrm{j}\omega_0n}=\cos{(\omega_0n)}+\mathrm{j}\sin{(\omega_0n)} \] 对于单位复指数序列,有 \[ |x(n)|=1\\ \arg[x(n)]=\omega_0n \]
信号的分解
最常见的离散信号分解是将其变为任意冲激序列的加权、延迟之和 \[ x(n)=\sum^{\infin}_{m=-\infin}x(m)\delta(n-m) \]
数学模型
数学模型
一个离散时间系统,其激励信号 \(x(n)\) 是一个序列,响应信号 \(y(n)\) 是另一个序列,图解可看作

同样在离散时间系统中我们也仅考虑线性、时不变系统,即 LTI 系统。
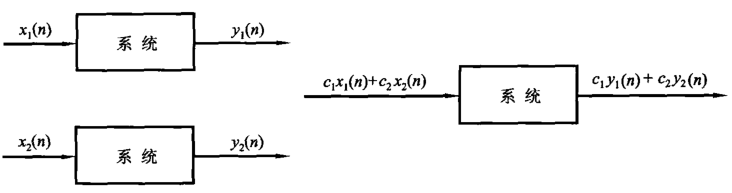
均匀性与叠加性
若输入为 \[
c_1x_1(n)+c_2x_2(n)
\] 那么输出为 \[
c_1y_1(n)+c_2y_2(n)
\] 
差分方程
在连续时间信号中,微分方程由连续信号的积分和微分线性叠加组成。
而在离散时间信号中,使用差分方程描述系统,其中差分方程由平移信号线性叠加组成,如 \(x(n+1),x(n+2),\cdots,x(n-1),x(n-2),\cdots\)。
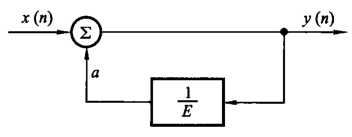
如图所示系统,我们可以写出差分方程 \[ y(n)-ay(n-1)=x(n) \] 这是一个常系数线性差分方程(difference equation),或称递归关系式(recurrence relation)。
一般情况下,差分方程等式左端由未知序列 \(y(n)\) 及其移位序列 \(y(n-1),y(n-2),\cdots\) 线性叠加组成。
标准化最高项为 \(y(n)\),如果方程移位项存在 \(y(n-N)\),\(N\) 最大,那么我们就称作这个差分方程为 \(N\) 阶差分方程。
微分
考虑对与连续时间系统,有 \[ \frac{\mathrm{d}}{\mathrm{d}t}y(t)\approx \frac{y[(n+1)T]-y(nT)}{T},T\approx0 \] 即当 \(T\) 较小时,满足连续时间模型的微分约等于差分方程形式。
即,在离散时间系统中,有 \[ \frac{y(n+1)-y(n)}{T}\approx Ay(n)+x(n) \]
常系数线性差分方程的求解
方程表示
常系数线性差分方程的一般形式可表示为 \[ a_0y(n)+a_1y(n-1)+\cdots+a_{N-1}y(n-N+1)+a_Ny(n-N)=\\ b_0x(n)+b_1x(n-1)+\cdots+b_{N-1}x(n-N+1)+b_Nx(n-N)\\ \sum^N_{k=0}a_ky(n-k)=\sum^M_{r=0}b_rx(n-r) \]
迭代法
依次迭代,通过数学归纳法得到解。
例如差分方程 \[ y(n+1)=ay(n)+x(n)\\ x(n)=\delta(n) \] 已知 \(n\geq 0\) 开始有信号。
那么,根据迭代法从 \(0\) 至 \(n\) 有 \[ y(0)=ay(-1)+1=1\\ y(1)=ay(0)+0=a\\ y(2)=ay(1)+0=a^2\\ \vdots\\ y(n)=ay(n-1)+0=a^n \] 因此可以归纳出 \[ y(n)=a^nu(n) \]
时域经典法
求解齐次解和特解,然后代入边界条件求解。
或者是求解零输入响应与零状态响应,利用卷积的方法求零状态响应即可。
首先,提取差分方程的特征方程,即 \[ a_0\lambda^N+a_1\lambda^{N-1}+\cdots+a_{N-1}\lambda+a_N=0 \] 我们将特征方程的解 \(\lambda_1,\lambda_2,\cdots,\lambda_N\) 称为差分方程的特征根。
在没有重根的情况下,差分方程的其次解为 \[ C_1\lambda_1^n+C_2\lambda_2^n+\cdots+C_N\lambda_N^n \] 如果存在重根,那么对于 \(K\) 阶重根的部分将改写为 \[ (C_1n^{K-1}+C_2n^{K-2}+\cdots+C_{K-1}n+C_K)\lambda_1^n \] 如果存在共轭复根 \(\lambda_1=\sigma+\mathrm{j}\omega,\lambda_2=\sigma-\mathrm{j}\omega\),那么将对共轭复根改写成 \[ e^{\sigma x}(C_1\cos{\omega x}+C_2\sin{\omega x}) \] 例如 \[ y(n)-2y(n-1)+2y(n-2)-2y(n-3)+y(n-4)=0 \] 列出特征方程 \[ \lambda^4-2\lambda^3+2\lambda^2-2\lambda+1=0\\ (\lambda-1)^2 (\lambda^2+1)=0 \] 求得 \[ \lambda_1=\lambda_2=1\\ \lambda_3=\mathrm{j},\lambda_4=-\mathrm{j} \] 可以写出齐次解形式 \[ y(n)=(C_1n+C_2)(1)^n+P\cos(\frac{n\pi}{2})+Q\sin{(\frac{n\pi}{2})} \] 特解的形式一般由激励信号决定,比如说差分方程 \[ y(n)+2y(n-1)=x(n)-x(n-1) \] 激励函数是 \(x(n)=n^2\)。
将激励函数代入,可得右端为 \[ 2n-1 \] 那么由系数一一对应可得,左端形式应该为 \[ D_1n+D_2 \] 代入比较系数可得 \[ 3D_1=2\\ 3D_2-2D_1=-1 \] 解得 \[ D_1=\frac{2}{3},D_2=\frac{1}{9} \] 零状态响应即 \(n<0\) 时,\(y(n)=0\) 的响应。
零输入响应与齐次解的形式相同,代入系统状态即可。