自动控制原理-线性系统的时域分析与校正
自动控制原理
线性系统的时域性能指标
时域分析法中的典型输入信号
动态性能
系统的动态性能是以系统阶跃响应为基础来衡量的。
| 动态性能指标 | 含义 | 图示 |
|---|---|---|
| 延迟时间 \(t_d\) | 阶跃响应第一次达到终值 \(h(\infty)\) 的 \(50\%\) 所需的时间 |  |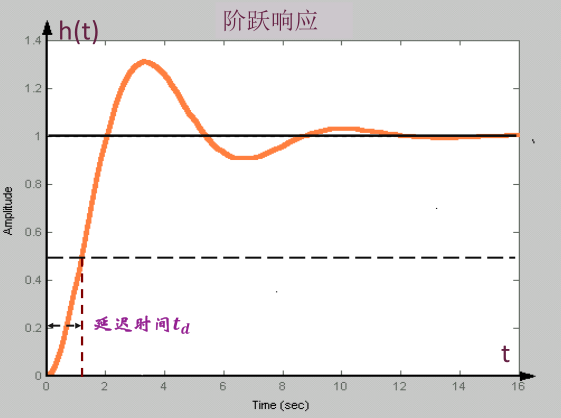
| 上升时间 \(t_r\) | 阶跃响应从终值的 \(10\%\) 上升到终值的 \(90\%\) 所需的时间；对有振荡的系统，也可以定义为从 0 到第一次达到终值所需的时间 |  |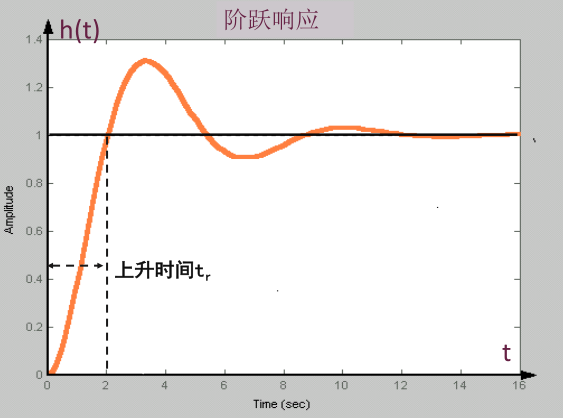
| 峰值时间 \(t_p\) | 阶跃响应越过终值 \(h(\infty)\) 达到第一个峰值所需的时间 |  |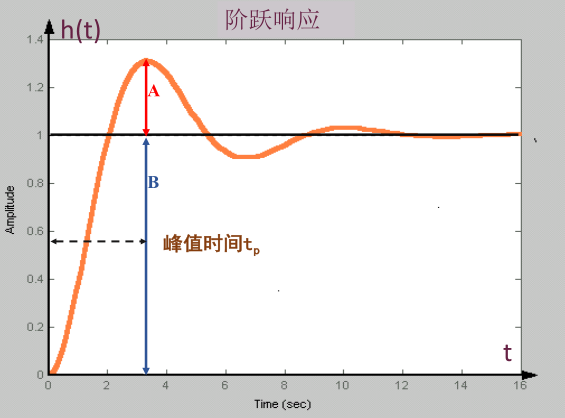
| 调节时间 \(t_s\) | 阶跃响应到达并保持在终值 \(h(\infty)\) 的 \(\pm5\%\) 误差带内所需的最短时间；有时也用终值的 \(\pm2\%\) 误差带来定义调节时间 |  |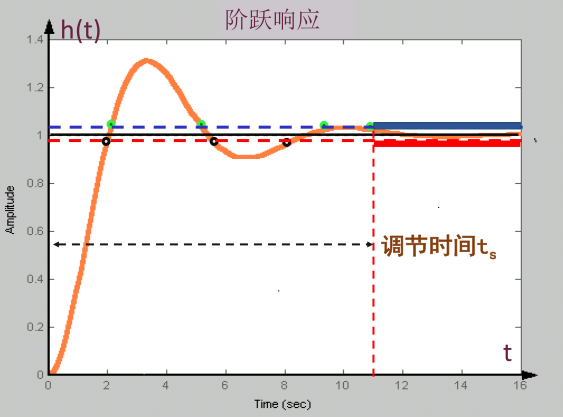
| 超调量 \(\sigma\%\) | 峰值 \(h(t_p)\) 超出终值 \(h(\infty)\) 的百分比 |  |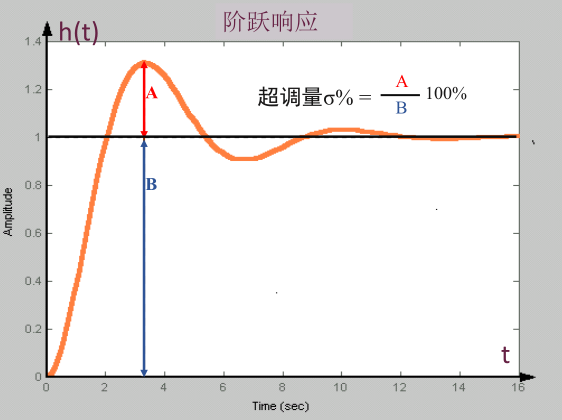
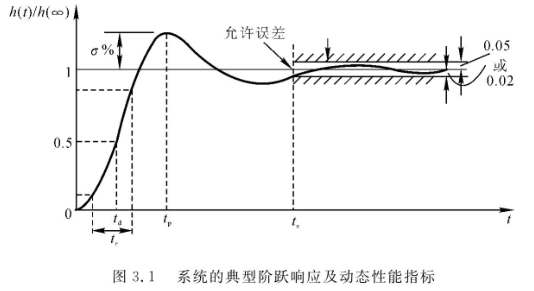
一阶系统时间响应及动态性能
传递函数标准型
开环传递函数 \[ G(s)=\frac{K}{s} \] 闭环传递函数 \[ \Phi(s)=\frac{\frac{K}{s}}{1+\frac{K}{s}}=\frac{1}{Ts+1},T=\frac{1}{K} \] 单位阶跃响应 \[ C(s)=\Phi(s)R(s)=\frac{1}{Ts+1}\frac{1}{s}=\frac{1}{s}-\frac{1}{s+1/T} \] 时域下的单位阶跃响应 \[ h(t)=\mathscr{L}^{-1}[C(s)]=1-e^{-\frac{t}{T}} \] 其中，\(K\) 称作开环增益，\(T\) 称作一阶系统的时间常数，系统特征根 \(\lambda=-1/T=-K\)。
动态性能指标计算
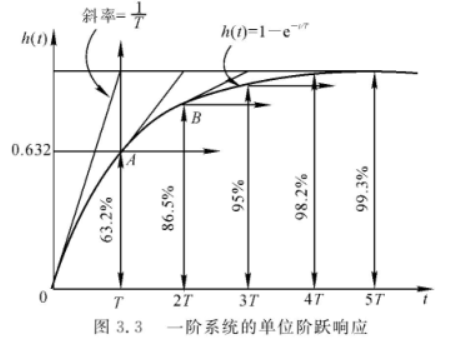
通过时域下单位阶跃响应的表达式，可知
\[
\begin{cases}
h(0)=0\\
h(\infty)=1\\
h'(0)=\frac{1}{T}\\
h'(t)=\frac{1}{T}e^{-\frac{t}{T}}
\end{cases}
\] 故一阶系统的调节时间 \(t_d\)： \[
h(t_s)=1-e^{-\frac{t_s}{T}}=0.95
\] 可解得 \[
t_s=3T
\] 同时可知系统超调量 \(\sigma\%\) 为 0。
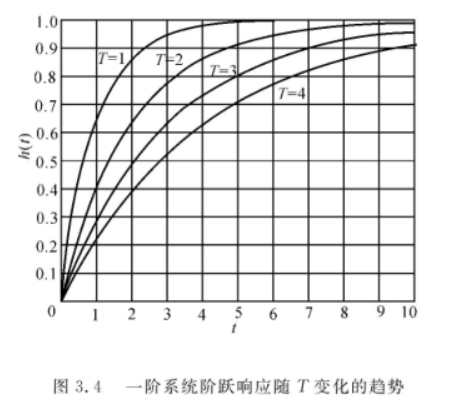
同时我们也知道，当 \(T\) 越大，调节时间越长，到达极点的时间越久。
一阶系统典型输入响应
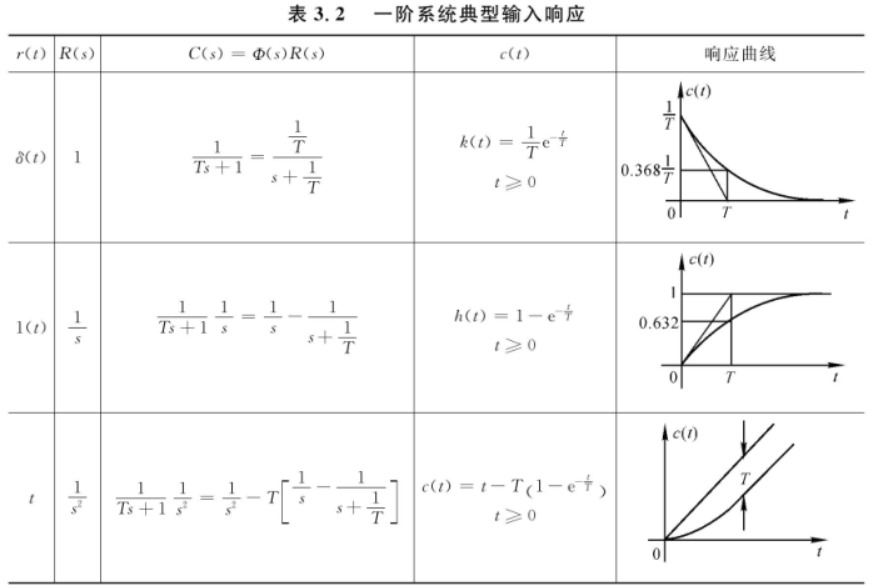
计算示例
示例一
原系统传递函数为 \[ G(s)=\frac{10}{0.2s+1} \] 采用下图的反馈方式，欲将反馈系统的调节时间减小为原来的 0.1，并且保证放大倍数不变，试确定参数 \(K_0,K_1\)。
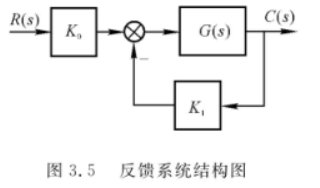
由原系统传递函数可得，
调节时间 \(t_s=0.6\)，系统增益 \(K=10\)。
改造后的系统调节时间 \(t'_s=0.1t_s=0.06=3T',K'=K=10\)。
可得现反馈系统的传递函数为 \[ \Phi(s)=\frac{K_0G(s)}{1+K_1G(s)}=\frac{\frac{10K_0}{1+10K_1}}{\frac{0.2}{1+10K_1}s+1} \] 有 \[ \begin{cases} \frac{10K_0}{1+10K_1}=K’=10\\ \frac{0.2}{1+10K_1}=T'=0.02 \end{cases} \] 解得 \[ \begin{cases} K_0=10\\ K_1=0.9 \end{cases} \]
示例二
已知单位反馈系统的单位阶跃响应 \(h(t)=1-e^{-at}\)，求解系统闭环传递函数 \(\Phi(s)\)，单位脉冲响应 \(k(t)\)，开环传递函数 \(G(s)\)。
我们知道单位脉冲响应就是单位阶跃响应的微分，即 \[ k(t)=h'(t)=ae^{-at} \] 而单位脉冲响应拉氏变换后便是系统的传递函数，即 \[ \Phi(s)=\mathscr{L}[k(t)]=\frac{a}{s+a} \] 又知道传递函数表达式为 \[ \Phi(s)=\frac{G(s)}{1+G(s)} \] 可以得到 \[ G(s)=\frac{\Phi(s)}{1-\Phi(s)}=\frac{a}{s} \]
二阶系统典型输入响应
传递函数标准型
开环传递函数 \[ G(s)=\frac{\omega_n^2}{s(s+2\xi\omega_n)} \] 闭环传递函数 \[ \begin{align} \Phi(s)&=\frac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2} & \text{(首1型)}\\ &=\frac{1}{T^2s^2+2T\xi s+1} & \text{(尾1型)} \end{align} \] 我们称，\(\xi\) 为阻尼比，\(\omega_n\) 为无阻尼自然频率，且满足 \[ T=\sqrt{\frac{T_0}{K}}\\ \omega_n=\frac{1}{T}\\ \xi=\frac{1}{2}\sqrt{\frac{1}{KT_0}} \] 首1标准型传递函数常用于时域分析中；尾1标准型常用于频域分析中。
我们知道，二阶系统闭环特征方程为 \[ D(s)=s^2+2\xi\omega_ns+\omega_n^2=0 \] 可以计算出不同的特征根 \(\lambda\)，按阻尼比 \(\xi\) 进行分类，得到
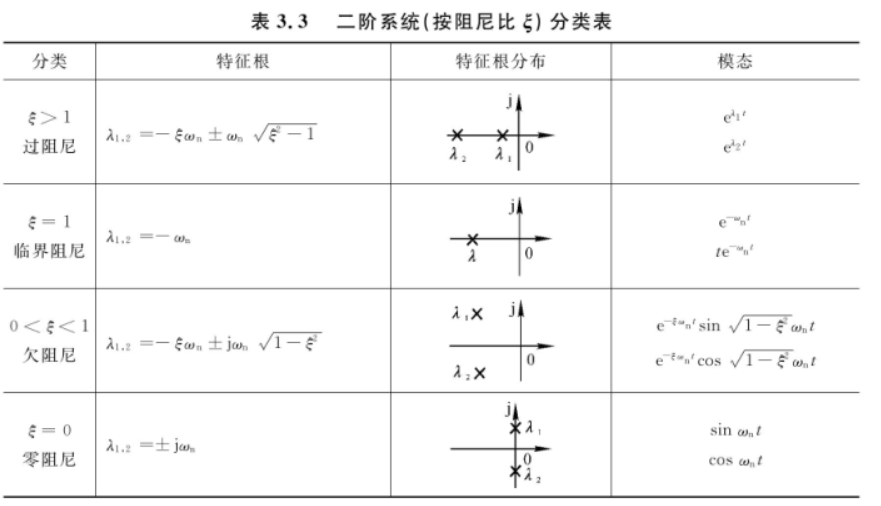
过阻尼动态性能指标计算
计算 \(D(s)=0\) 得到 \[ \lambda_1=-\frac{1}{T_1}=-(\xi-\sqrt{\xi^2-1})\omega_n\\ \lambda_2=-\frac{1}{T_2}=-(\xi+\sqrt{\xi^2-1})\omega_n\\ (T_1>T_2) \] 那么得到单位阶跃响应为 \[ C(s)=\Phi(s)R(s)=\frac{\omega_n^2}{(s+1/T_1)(s+1/T_2)}\frac{1}{s} \] 拉氏反变换得到 \[ h(t)=1+\frac{e^{-\frac{t}{T_1}}}{\frac{T_2}{T_1}-1}+\frac{e^{-\frac{t}{T_2}}}{\frac{T_1}{T_2}-1} \] 求解调节时间，即 \[ h(t_s)=1+\frac{1}{\frac{T_2}{T_1}-1}e^{-\frac{t_s}{T_1}}+\frac{1}{\frac{T_1}{T_2}-1}e^{-\frac{T_1}{T_2}\frac{t_s}{T_1}}=0.95 \] 我们可以计算得到 \[ \xi=\frac{1+T_1/T_2}{2\sqrt{T_1/T_2}} \] 根据 \(h(t_s)\) 绘制 \(t_s/T_1-T_1/T_2\) 图
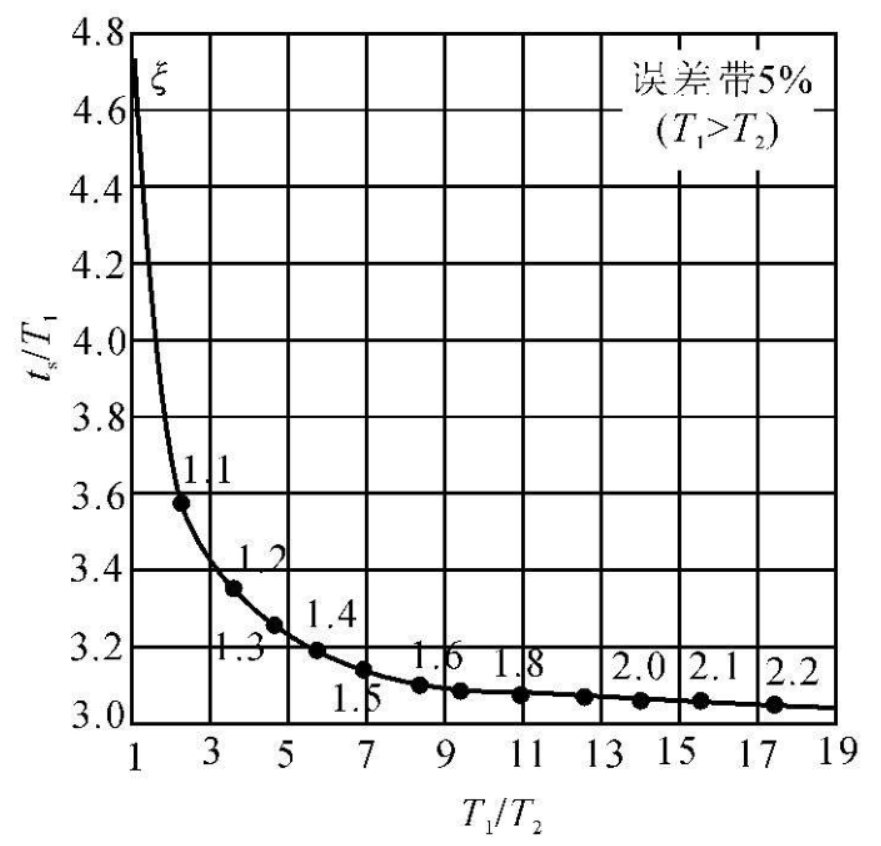
根据图，我们便可求出 \(t_s\)。
计算示例
示例一
已知闭环传递函数 \[ \Phi(s)=\frac{16}{s^2+10s+16} \] 计算系统动态性能指标。
由系统闭环传递函数可得， \[ \Phi(s)=\frac{16}{(s+2)(s+8)}\\ \omega_n=\sqrt{16}=4\\ T_1=\frac{1}{2}\\ T_2=\frac{1}{8}\\ T_1/T_2=4\\ \xi=\frac{1+4}{2\times\sqrt{4}}=1.25>1\\ \] 由图可知，\(t_s/T_1=3.3\)，故 \[ t_s=3.3T_1=1.65\ \mathrm{s} \]
临界阻尼性能指标计算
当 \(\xi=1\) 时，系统处于临界阻尼状态，此时闭环极点是一对相等实根，即 \[ \lambda_1=\lambda_2=-\omega_n=-1/T_1 \] 其中，单位阶跃响应为 \[ C(s)=\Phi(s)R(s)=\frac{\omega_n^2}{(s+\omega_n)^2}\frac{1}{s} \] 故时域下 \[ h(t)=1-(1+\omega_nt)e^{-\omega_nt} \] 可以求解得到调节时间 \(t_s=4.75T_1\)。
欠阻尼性能指标计算
欠阻尼系统的极点可以用两种形式表示。
直角坐标表示 \[ \lambda=\sigma\pm\mathrm{j}\omega_d=-\xi\omega_n\pm\mathrm{j}\sqrt{1-\xi^2}\omega_n \]
极坐标表示 \[ \begin{cases} |\lambda|=\omega_n\\ \angle \lambda=\beta \end{cases}, \begin{cases} \cos\beta=\xi\\ \sin\beta=\sqrt{1-\xi^2} \end{cases} \]
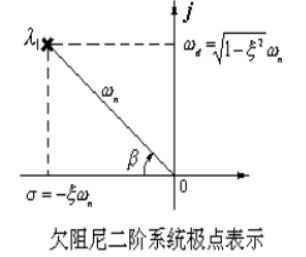
单位阶跃响应可得 \[ h(t)=1-\frac{e^{-\xi\omega_nt}}{\sqrt{1-\xi^2}}\sin(\sqrt{1-\xi^2}\omega_nt+\beta) \] 其曲线被上下包络线 \(1+\frac{e^{-\xi\omega_nt}}{\sqrt{1-\xi^2}}\) 和 \(1-\frac{e^{-\xi\omega_nt}}{\sqrt{1-\xi^2}}\) 包络。
计算调节时间变为计算上下包络线进入 \(5\%\) 误差带的时间 \[ \left|1-(1-\frac{e^{-\xi\omega_nt}}{\sqrt{1-\xi^2}})\right|=\frac{e^{-\xi\omega_nt}}{\sqrt{1-\xi^2}}=0.05 \] 计算可得 \[ t_s=\frac{3.5}{\xi\omega_n} \]
当 \(0.3<\xi<0.8\) 时才可用。
当 \(\xi=0.707(\beta=45\degree)\) 时，\(t_s\approx2T\)，故被称作最佳阻尼比。
峰值时间 \[
t_p=\frac{\pi}{\sqrt{1-\xi^2}\omega_n}
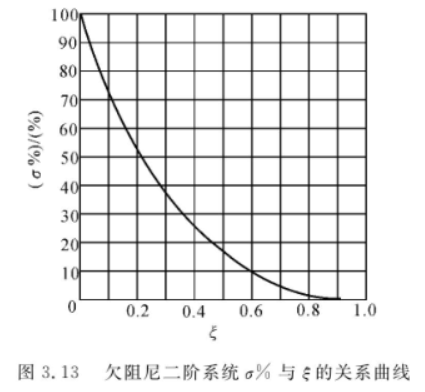
\] 超调量 \[
\sigma\%=e^{-\xi\pi/\sqrt{1-\xi^2}}\times100\%
\] 