自动控制原理-控制系统数学模型

发表于 2023-04-07 更新于 2023-06-22 本文字数： 10k 阅读时长 ≈ 9 分钟

有关control-system-mathematical-model的简要笔记

自动控制原理

控制系统的数学模型

一般来说，可以使用数学模型解决的问题普遍为线性时不变系统（定常系统）。

即一般只考虑微分方程为以下形式 \[ a_n\frac{\mathrm{d}^nr(t)}{\mathrm{d}t^n}+a_{n-1}\frac{\mathrm{d}^{n-1}r(t)}{\mathrm{d}t^{n-1}}+\cdots+a_0r(t)=b_n\frac{\mathrm{d}^nc(t)}{\mathrm{d}t^n}+b_{n-1}\frac{\mathrm{d}^{n-1}c(t)}{\mathrm{d}t^{n-1}}+\cdots+b_0c(t) \] 其中 \(r(t)\) 为输入，\(c(t)\) 为输出。

对非线性定常系统我们通常使用神经网络、机器学习的手段进行建模。

时域数学模型

线性系统

建立

根据系统的具体工作情况，确定系统或原部件的输入、输出变量
从输入开始，按照信号传递顺序，依据各变量所遵循的物理（或化学）定律，写出各元件的动态方程，通常是微分方程
联立方程消去中间变量，写出关于输入、输出变量的微分方程式
将微分方程标准化（即写成左输出右输入的形式，构建标准微分方程）

R-L-C 无源网络

写出输入电压 \(u_\tau\) 与输出电压 \(u_c\) 之间的微分方程。

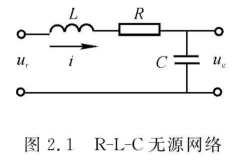
R-L-C 无源网络

由基尔霍夫定律写出电路的电压平衡方程： \[ u_{r}(t)=L \frac{\mathrm{d} i(t)}{\mathrm{d} t}+R i(t)+u_{c}(t) \] 可知 \[ i(t)=C\frac{\mathrm{d}u_c(t)}{\mathrm{d}t} \] 联立后消去中间变量 \(i(t)\) 可得： \[ LC\frac{\mathrm{d}^{2} u_{c}(t)}{\mathrm{d} t^{2}}+RC\frac{\mathrm{d} u_{c}(t)}{\mathrm{d} t}+u_{c}(t)=u_{r}(t) \] 可知最终表达式为二阶线性常系数微分方程。

弹簧-质量-阻尼器系统

\(K\) 为弹簧的弹性系数，\(f\) 为阻尼器的阻尼系数，\(m\) 表示小车质量。忽略小车与地面的摩擦，写出输入外力 \(F(t)\) 与输出位移 \(y(t)\) 的系统微分方程。

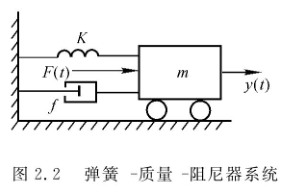
受力分析得：

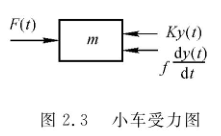
由牛顿第二定律可得： \[ F(t)-f \frac{\mathrm{d} y(t)}{\mathrm{d} t}-K y(t)=m \frac{\mathrm{d}^{2} y(t)}{\mathrm{d} t^{2}} \] 整理可得： \[ \frac{\mathrm{d}^{2} y(t)}{\mathrm{d} t^{2}}+\frac{f}{m} \frac{\mathrm{d} y(t)}{\mathrm{d} t}+\frac{K}{m} y(t)=\frac{F(t)}{m} \] 可知最终表达式为二阶线性常系数微分方程。

直流电动机转速闭环控制系统

取给定电压 \(u_r(t)\) 为输入量，转速 \(\omega(t)\) 为输出量。

从产生偏差的元件开始，按信号流动方向依次写出回路中各元件的微分方程。

（1）测量元件

测速发电机（图中以 TG 标注）作为测量元件，将系统输出角速度 \(\omega(t)\) 转换成相应的电压 \(u_f(t)\) 进行反馈，有 \[ u_f(t)=K_t\omega(t) \] 其中，\(K_t\) 是测速发电机的传递函数。

（2）比较电路

比较电路的作用是将测速发电机的反馈电压 \(u_f(t)\) 与给定电压 \(u_r(t)\) 进行比较，产生偏差电压 \(u_e(t)\)，即 \[ u_e(t)=u_r(t)-u_f(t) \] （3）放大部件

包括两级运算放大器喝一级功率放大器，用于放大偏差电压 \(u_e(t)\)，各级放大器方程分别为

第一级放大器： \[ u_{1}(t)=\frac{R_{2}}{R_{1}} u_{e}(t) \]
第二级放大器： \[ u_{2}(t)=\frac{R_{4}}{R_{3}} u_{1}(t) \]
功率放大器： \[ u_{a}(t)=K_{3} u_{2}(t) \]

不妨简写成 \[ u_a(t)=K_Au_e(t) \] 其中 \[ K_{A}=\frac{R_{2} R_{4}}{R_{1} R_{3}} K_{3} \] （4）直流发电机

直流发电机将电枢电压 \(u_a(t)\) 转换成电动机转子轴的角速度 \(\omega_m(t)\)，即 \[ T_{m} \frac{\mathrm{d} \omega_{m}(t)}{\mathrm{d} t}+\omega_{m}(t)=K_{a} u_{a}(t) \] （5）减速器

用于降低发电机的输出转速，增大转矩。减速器方程为 \[ \frac{\omega(t)}{\omega_m(t)}=\frac{1}{i} \] 其中，\(i\) 是减速器的传动比。

联立以上式子，消去中间变量可得 \[ \frac{\mathrm{d}\omega(t)}{\mathrm{d}t}+\frac{i+K_AK_aK_t}{T_mi}\omega(t)=\frac{K_AK_a}{T_mi}u_r(t) \] 可知最终表达式为一阶线性常系数微分方程。

总结

将以上具有相同数学模型的不同物理系统称为相似系统，相似原理揭示了不同物理现象的相似关系，为控制系统的分析、设计和计算机仿真奠定了基础。

非线性系统

严格地说，实际系统的数学模型一般都是非线性的，例如弹簧的刚度和形变有关，不一定是常数；而电阻、电感、电容等参数值与温度、压力、电流等有关系。所以一般情况下，会将非线性系统在合理、可能的条件下简化为线性系统。

铁芯线圈系统

写出以电压 \(u_r\) 为输入，电流 \(i\) 为输出的铁芯线圈的线性化方程。

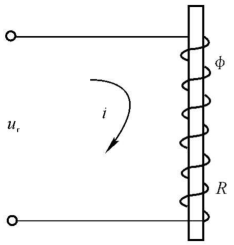
根据基尔霍夫定律，有 \[ u_r=u_1+Ri \] 其中 \(u_1\) 为线圈的感应电动势，由法拉第电磁感应效率可知 \[ u_1=K_1\frac{\mathrm{d}\phi(i)}{\mathrm{d}t}=K_1\frac{\mathrm{d}\phi(i)}{\mathrm{d}i}\frac{\mathrm{d}i}{\mathrm{d}t} \] 其中 \(K_1\) 为比例常数（线圈匝数）。

知晓磁通 \(\phi\) 与电流 \(i\) 不构成线性函数，可能的图如下：

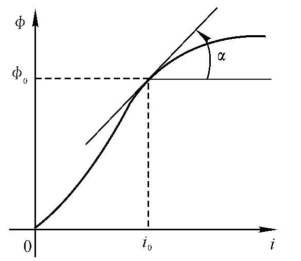
如果在工作范围内，仅取 \(\mathrm{d}i\) 的变化，（在工作点 \((i_0,\phi_0)\)）得到 \(\phi\) 的近似值为 \[ \phi=\phi_0+\phi'(i_0)\mathrm{d}i \] 即将 \(\phi\) 当作与 \(i\) 的线性函数，有 \[ \frac{\mathrm{d}\phi(i)}{\mathrm{d}i}=C_1=\phi'(i_0) \] 整理可得 \[ K_1\phi'(i_0)\frac{\mathrm{d}i}{\mathrm{d}t}+Ri=u_r \] 即为一阶常系数微分方程。

运动的模态

线性微分方程的解由齐次方程的通解和给定信号对应的特解组成，而其中通解反映了系统自由运动的规律。

如果微分方程的特征根为 \(\lambda_1,\lambda_2,\cdots,\lambda_n\)，且无重根，则把函数 \(e^{\lambda_1t},e^{\lambda_2t},\cdots,e^{\lambda_nt}\) 称作该微分方程所描述运动的模态，也叫振态。

如果有重根 \(\lambda\)，则模态是具有 \(t^ke^{\lambda t}\) 形式的函数，其中 \(k\in\Z^*\) （具体为 \(k+1\) 为重根数）。

如果特征根中有共轭复根 \(\lambda=\sigma\pm j\omega\)，则其共轭复模态为 \(e^{(\sigma\pm j\omega)t}\)，或者是写成实函数模态 \(e^{\sigma t}\sin{\omega t},e^{\sigma t}\cos{\omega t}\)。

每一种模态都可以看成是线性系统自由响应最基本的运动形态，线性系统的自由响应就是其相应模态的线性组合。

微分方程求解方法

特征根法

微分方程的特征根是将方程中的 \(n\) 阶导数 \(f^{(n)}(x)\) 替换成 \(n\) 阶多项式 \(x^n\) 后的多项式方程的解。

例如存在二阶常系数齐次线性微分方程 \(y''+py'+qy=0\)，特征方程为 \(x^2+px+q=0\)，如果

\(p^2-4q>0\)，相异实根为 \(\lambda_1,\lambda_2\)，则方程有两个线性无关的解 \(y_1=e^{\lambda_1x},y_2=e^{\lambda_2x}\)，通解为 \(C_1e^{\lambda_1 x}+C_2e^{\lambda_2 x}\)
\(p^2-4q=0\)，重根 \(\lambda=\lambda_1=\lambda_2=-\frac{p}{2}\)，则方程有一个解为 \(y=xe^{\lambda x}\)（另一个解为 \(y=e^{\lambda x}\)），通解为 \(y=(C_1+C_2x)e^{\lambda x}\)
\(p^2-4q<0\)，共轭复根 \(\lambda=\alpha\pm i\beta\)，则方程有两个线性无关的解 \(y_1=e^{(\alpha+i\beta)x},y_2=e^{(\alpha-i\beta)x}\)，通解为 \(y=e^{\alpha x}(C_1\cos{\beta x}+C_2\sin{\beta x})\)

这样我们就通过特征根解得微分方程的通解。

拉普拉斯变换

拉普拉斯变换简称拉氏变换，是将实函数转化为 \(Re\ s>0\) 的复函数，定义为 \[ F(s)=\int^{+\infty}_0f(t)e^{-st}dt \] 本质是将时域函数转化为等价的复域函数，简单用 \(F(s)=\mathscr{L}[f(t)]\) 表示对时域函数 \(f(t)\) 进行拉普拉斯变换。

常用的变换结果有 \[ \mathscr{L}(1)=\mathscr{L}[u(t)]=\frac{1}{s}\\ \mathscr{L}(t^n)=\frac{n!}{s^{n+1}}\\ \mathscr{L}(e^{kt})=\frac{1}{s-k}\\ \mathscr{L}(t^ne^{kt})=\frac{n!}{(s-k)^{n+1}}\\ \mathscr{L}(tf(t))=(-1)\frac{\mathrm{d}}{\mathrm{d}s}f(s)=-f'(s)\\ \mathscr{L}(t^nf(t))=(-1)^n\frac{\mathrm{d}^n}{\mathrm{d}s^n}f(s)=(-1)^nf^{(n)}(s)\\ \mathscr{L}(\cos{(\omega_0 t)})=\frac{s}{s^2+\omega_0^2}\\ \mathscr{L}(\sin{(\omega_0 t)})=\frac{\omega_0}{s^2+\omega_0^2} \] 由此可知，拉普拉斯变换有以下一些性质

线性性质 \[ \alpha f_1(t)\pm \beta f_2(t)\leftrightarrow \alpha F_1(s)\pm \beta F_2(s) \]
位移性质（复位移） \[ f(t)\cdot e^{s_0t}\leftrightarrow F(s-s_0) \]
延迟性质（时位移，一般只考虑向右平移） \[ f(t-t_0)\cdot u(t-t_0)\leftrightarrow F(s)\cdot e^{-st_0} \]
微分性质 \[ f'(t)\leftrightarrow sF(s)-f(0) \]

对于高阶微分，有 \[ f^n(t)\leftrightarrow s^nF(s)-s^{n-1}F(0)-s^{n-2}f'(0)-\cdots-f^{n-1}(0) \]
积分性质 \[ \newcommand{\diff}{\mathrm{d}} \int^t_0f(\tau)\diff{\tau}\leftrightarrow \frac{F(s)}{s}+\frac{f^{-1}(0)}{s} \]

在这里 \(f^{-1}\) 表示 \(\int f\)，即对 \(f(t)\) 进行积分。

初值定理 \[ \lim_{t\to0}f(t)=\lim_{s\to\infty}s\cdot F(s) \]
终值定理 \[ \lim_{t\to\infty}f(t)=\lim_{s\to0}s\cdot F(s) \]

拉普拉斯逆变换

公式定义如下 \[ \newcommand{\j}{\mathrm{j}} f(t)=\frac{1}{2\pi\j}\int^{\sigma+\j\infty}_{\sigma-\j\infty}F(s)e^{ts}\diff{s} \] 一般我们不会使用定义法，而是将其进行裂项后用公式得结果。

例如 \[ F(s)=\frac{1}{s(s+a)} \] 裂项后得到 \[ F(s)=\frac{1}{a}\left(\frac{1}{s}-\frac{1}{s+a}\right) \] 通过公式得到 \[ f(t)=\frac{1}{a}(1-e^{-at}) \] 也可以使用留数法求解裂项，例如 \[ F(s)=\frac{1}{s(s+1)^2}=\frac{A}{s}+\frac{B}{s+1}+\frac{C}{(s+1)^2} \]

在这里裂项后一定是每个项数都存在。

那么 \[ A=\lim_{s\to0}sF(s)=1\\ B=\lim_{s\to1}(s+1)^2F'(s)=-1\\ C=\lim_{s\to1}(s+1)^2F(s)=1 \] 有 \[ f(t)=1-e^{-t}+te^{-t} \]

拉氏变换法

例如控制系统微分方程如下 \[ y''(t)+2y'(t)+y(t)=1(t)\\ y(0)=y'(0)=0 \]

\(1(t)\) 即阶跃信号 \(u(t)\)。

对该微分方程进行拉氏变换 \[ (s^2+2s+1)Y(s)=\frac{1}{s} \]

根据微分性质，例如

\(\mathscr{L}[y''(t)]=s^2Y(s)-y'(0)=s^2Y(s)\)

求解得到 \[ Y(s)=\frac{1}{s(s^2+2s+1)} \] 进行拉氏反变换得到 \[ f(t)=1-e^{-t}+te^{-t} \]

复域数学模型

传递函数

我们已知线性定常系统的微分方程一般可写为 \[ a_n\frac{\mathrm{d}^nr(t)}{\mathrm{d}t^n}+a_{n-1}\frac{\mathrm{d}^{n-1}r(t)}{\mathrm{d}t^{n-1}}+\cdots+a_0r(t)=b_n\frac{\mathrm{d}^nc(t)}{\mathrm{d}t^n}+b_{n-1}\frac{\mathrm{d}^{n-1}c(t)}{\mathrm{d}t^{n-1}}+\cdots+b_0c(t) \] 对两端进行拉普拉斯变换，可得 \[ (a_ns^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0)R(s)=(b_ns^n+b_{n-1}s^{n-1}+\cdots+b_1s+b_0)C(s) \] 定义，系统的传递函数为 \[ \frac{C(s)}{R(s)}=\frac{b_ns^n+b_{n-1}s^{n-1}+\cdots+b_1s+b_0}{a_ns^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0} \] 即输出量的拉氏变换与输入量的拉氏变换之比。

传递函数定义在零初始条件下，即

输入是在 \(t=0\) 以后才作用于系统的，即当 \(t\leq0\) 时，输入量及其各阶导数均为 0。
输入作用于系统之前，当 \(t\leq0\) 时，输出量及其各阶导数均为 0。

这样定义有利于简化运算和比较系统性能。

增益

根据传递函数的不同，我们可以把传递函数标准化。

首先要有一个前提，在负反馈闭环系统的传递函数中，分子的次数要低于分母的次数。

有两种标准化方式：

首 1 标准型：分母的最高次数的系数为 1。
尾 1 标准型：分子和分母的常系数为 1。

首 1 标准型主要应用于根轨迹的绘制；而尾 1 标准型主要应用于 bode 图的绘制。

一般尾 1 标准型的整体系数是我们关注的增益。

例如 \[ G(s)=\frac{4s-4}{s^3+3s^2+2s}=2\cdot\frac{s-1}{s(\frac{1}{2}s+1)(s+1)} \] 故我们称这个系统的增益为 \(K=2\)。

传递函数的性质

传递函数的性质：

由于实际上的物理系统总是存在惯性，并且能源功率有限，所以实际系统的传递函数的分母阶次总是大于或等于分子阶次。
传递函数只取决于系统或元件自身的结构和参数，与输入输出无关
传递函数与微分方程有直接联系
记 \(k(t)\) 为系统单位脉冲响应，那么 \(G(s)=\mathscr{L}[k(t)]\)，即系统的传递函数是系统单位脉冲响应的拉氏变换
\(G(s)\) 与 \(s\) 复平面上的零极点图相对应

传递函数 \(G(s)\) 分子为零的解为零点，分母为零的解为极点。

传递函数的局限性：

传递函数的定义在零初始条件下，故不能反映非零初始条件下系统的全部运动规律
传递函数只适合于描述单变量系统（单输入-单输出）
传递函数是由拉氏变换定义的，只适用于定常系统

实例

R-L-C 无源网络

已知系统微分方程为 \[ LC\frac{\mathrm{d}^{2} u_{c}(t)}{\mathrm{d} t^{2}}+RC\frac{\mathrm{d} u_{c}(t)}{\mathrm{d} t}+u_{c}(t)=u_{r}(t) \] 对两端取拉氏变换可得传递函数为 \[ G(s)=\frac{U_c(s)}{U_r(s)}=\frac{1}{LCs^2+RCs+1} \]

电位器

电位器可以把线位移或角位移变换成电压量。

单个电位器常用作信号变换装置。

一对电位器可组成误差检测器。

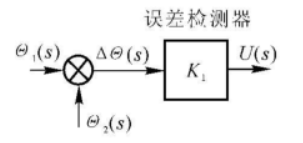
其中电位器的传递系数（传递常数）记为 \(K_1\)，即 \[ G(s)=\frac{U(s)}{\Delta\Theta(s)}=K_1 \] 需要注意的是电位器会有负载效应，即在元件输出端接有负载时所产生的影响，此时输出电压 \(u(t)\) 与电刷角位移 \(\theta(t)\) 不再保持线性关系，如果负载电阻 \(R_L\) 很大，则可以近似得到 \[ u(t)\approx K_1\theta(t) \]

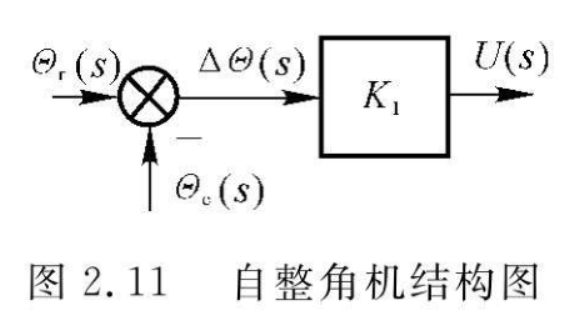
自整角机

自整角机是角位移传感器，在随动系统中总是成对使用的。按照用途不同分为力矩式和控制式。

自整角机的传递系数（传递常数）记为 \(K_s\)，即 \[ e(t)=K_s\cos{\Delta\theta}\sin{\omega t} \] 在 \(\Delta \theta\) 较小的情况下，近似有 \[ E\approx K_s\Delta\theta \] 自整角机与电位器组成的误差角检测器有相同的功能，故功能框图形式相同

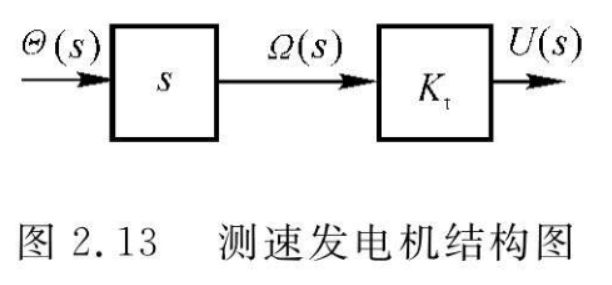
测速发电机

测速发电机的转子与待测设备的转轴相连，无论是直流或交流测速发电机，其输出电压均正比于转子的角速度，故其微分方程可写为 \[ u=K_t\omega=K_t\frac{\mathrm{d}\theta}{\mathrm{d}t} \] 其中 \(K_t\) 是测速发电机输出电压的斜率，也是传递常数。

其传递函数为 \[ G(s)=\frac{U(s)}{\Theta(s)}=K_t \] 或者为 \[ G(s)=\frac{U(s)}{\Theta(s)}=K_ts \] 当输入量取转速 \(\omega(t)\) 时用前者；输入量取转角 \(\theta(t)\) 时用后者。

电枢控制式直流电动机

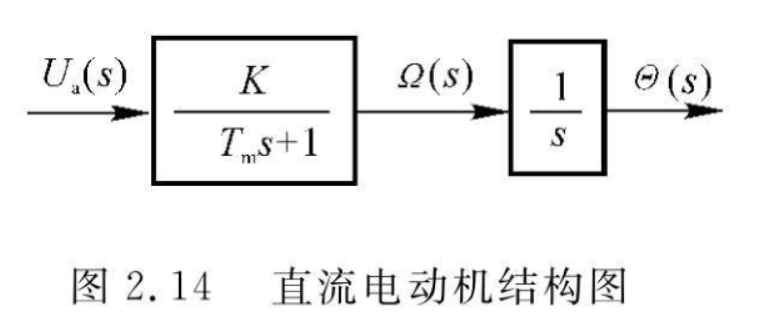
直流电动机的微分方程为 \[ T_{m} \frac{\mathrm{d} \omega_{m}(t)}{\mathrm{d} t}+\omega_{m}(t)=K_{a} u_{a}(t) \] 直流电动机结构图

得到电枢控制直流电动机的传递函数为 \[ G_a(s)=\frac{\Omega(s)}{U_a(s)}=\frac{K_a}{T_ms+1} \] 如果输出用角位移 \(\theta(t)\) 表示，则传递函数可以表示为 \[ G_a(s)=\frac{\Omega(s)}{U_a(s)}=\frac{K_a}{s(T_ms+1)} \]

两相异步电动机

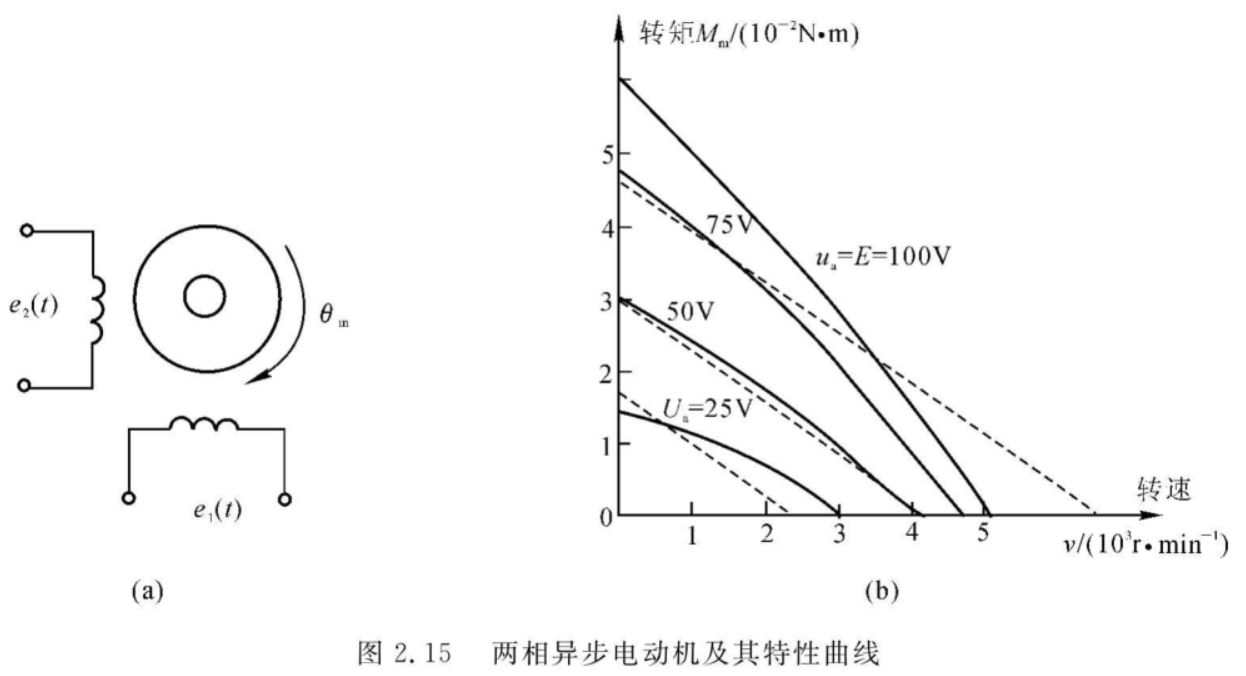
通常机械特性的线性化方程可表示为： \[ M_m=-C_\Omega\omega_m+M_s \] 其中，\(M_m\) 为电动机输出转矩；\(\omega_m\) 为电动机角速度；\(C_\Omega\) 为粘性摩擦系数；\(M_m\) 为堵转转矩。

例题

题干

已知某系统在零初始条件下的单位阶跃响应为 \[ c(t)=1-\frac{2}{3}e^{-t}-\frac{1}{3}e^{-4t} \] 求

系统的传递函数
系统的增益
系统的特征根及相应的模态
画出对应的零极点图
求系统的单位脉冲响应
求系统微分方程
当 \(c(0)=-1,c'(0)=0,r(t)=1(t)\) 时，系统的响应

系统的传递函数

系统的传递函数定义在零初始条件下，同时由传递函数的定义得知 \[ G(s)=\frac{C(s)}{R(s)} \] 其中，\(C(s)\) 是响应（输出）的拉氏变换方程，\(R(s)\) 是激励（输入）的拉氏变换方程。

对零初始条件下的单位阶跃响应进行拉氏变换，得到 \[ C(s)=\frac{1}{s}-\frac{2}{3}\frac{1}{s+1}-\frac{1}{3}\frac{1}{s+4}=\frac{2(s+2)}{s(s+1)(s+4)} \] 我们知道激励信号 \(r(t)=1(t)\)，那么其拉氏变换 \[ R(s)=\frac{1}{s} \] 故 \[ G(s)=\frac{2(s+2)}{(s+1)(s+4)} \]

系统的增益

由尾 1 标准型得知，系统的增益 \[ K=\frac{2\times2}{4}=1 \]

系统的特征根及其模态

由系统零初始条件下的单位阶跃响应可以得知，模态有 \[ e^{-t},e^{-4t} \] 故得知其特征根为 \[ \lambda_1=-1,\lambda_2=-4 \]

在这里也可以通过传递函数分母的解得知，传递函数分母的解为系统的特征根。

零极点图

传递函数 \(G(s)\) 分子为零的解为零点，分母为零的解为极点。

那么我们可以知道，极点有 \(-1,-4\)；零点有 \(-2\)。

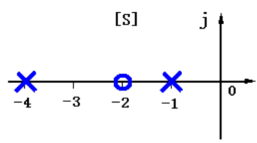
单位脉冲响应

我们由传递函数的性质可知，传递函数就是系统单位脉冲响应的拉氏变换，即 \[ \mathscr{L}[k(t)]=G(s) \] 那么我们对传递函数进行拉氏逆变换，有 \[ G(s)=\frac{2}{3}\frac{1}{s+1}+\frac{4}{3}\frac{1}{s+4}\\ k(t)=\mathscr{L}^{-1}[G(s)]=\frac{2}{3}e^{-t}+\frac{4}{3}e^{-4t} \]

在信号与系统中，我们也可以知道，单位脉冲响应就是单位阶跃响应的微分。

系统微分方程

我们化一下传递函数，得到 \[ (s^2+5s+4)C(s)=(2s+4)R(s) \] 对方程两边进行拉氏逆变换（零初始条件），得到 \[ c''(t)+5c'(t)+4c(t)=2r'(t)+4r(t) \]

系统的响应

对系统微分方程进行拉氏变换（有初始条件），得到 \[ [s^2C(s)-sc(0)-c'(0)]+5[sC(s)-c(0)]+4C(s)=2(s+2)R(s) \] 我们进行化简得到 \[ C(s)=\frac{2(s+2)}{s^2+5s+4}\frac{1}{s}-\frac{s+5}{s^2+5s+4}=\frac{-s^2-3s+4}{s(s+1)(s+4)} \] 其中自由相应部分（零输入响应）为 \[ C_0(s)=-\frac{s+5}{(s+1)(s+4)}=\frac{-4}{3}\frac{1}{s+1}+\frac{1}{3}\frac{1}{s+4} \] 故 \[ c_0(t)=\frac{-4}{3}e^{-t}+\frac{1}{3}e^{-4t} \] 而零初始条件下的单位阶跃响应（零状态响应）题目已经给出，故 \[ c(t)=(1-\frac{2}{3}e^{-t}-\frac{1}{3}e^{-4t})+(\frac{-4}{3}e^{-t}+\frac{1}{3}e^{-4t})=1-2e^{-t} \]