最优化方法——基于导数的优化

发表于 更新于 本文字数： 3k 阅读时长 ≈ 3 分钟
有关基于导数的最优化方法的简要笔记

最优化方法

基于导数的优化方法

梯度下降法

梯度下降法，也称最速下降法。

可以从另一篇博客中了解详细内容。

算法描述如下

  1. 选取初始点 \(\mathrm{x}_1\in R^n\)，容许误差 \(0\leq \epsilon\ll 1\)，令 \(k=1\)。
  2. 计算梯度 \(\mathrm{g}_k=\nabla f(\mathrm{x}_k)\)，如果 \(\|\mathrm{g}_k\|\leq \epsilon\)，算法停止，输出 \(\mathrm{x}_k\) 为近似最优解；否则继续。
  3. 取下降方向为梯度负方向 \(\mathrm{d}_k=-\mathrm{g}_k\)。
  4. 由线搜索技术确定步长 \(\alpha_k\)。
  5. 令 \(\mathrm{x}_{k+1}=\mathrm{x}_k+\alpha_k\mathrm{d}_k\)，同时 \(k=k+1\)，回到第二步。
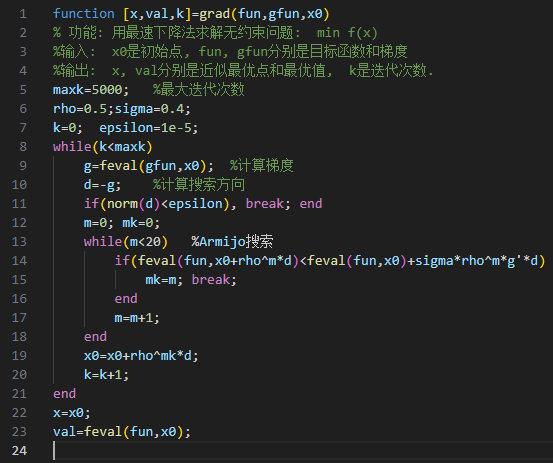
梯度下降法matlab代码

梯度下降法往往是局部最优解，所以对于许多问题并不是最优的下降算法。

但是在神经网络的优化方法中，梯度下降法表现优异。

牛顿下降法

在另一篇博客中也可以略见一二。

牛顿迭代法的基本公式是 \[ x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)} \] 这种算法的下降速度是极快的，对于许多优化问题都会选择牛顿法求解。

例如平方根倒数问题。

基于牛顿法和最速下降法，改进出牛顿下降法公式为 \[ \mathrm{x}_{k+1}=\mathrm{x}_k-\nabla^2f(\mathrm{x}_k)^{-1}\nabla f(\mathrm{x}_k) \]

为方便理解可以表示成 \[ \mathrm{x}_{k+1}=\mathrm{x}_k-\frac{\nabla f(\mathrm{x}_k)}{\nabla^2f(\mathrm{x}_k)} \] 即比值为一次导和二次导的比值。

算法描述如下：

  1. 选取初始点 \(\mathrm{x}_1\in R^n\)，容许误差 \(0\leq \epsilon\ll 1\)，令 \(k=1\)。
  2. 计算梯度 \(\mathrm{g}_k=\nabla f(\mathrm{x}_k)\)，如果 \(\|\mathrm{g}_k\|\leq \epsilon\)，算法停止，输出 \(\mathrm{x}_k\) 为近似最优解；否则继续。
  3. 计算 \(\mathrm{G}_k=\nabla^2 f(\mathrm{x}_k)\)，求解线性方程得到 \(\mathrm{d}_k:\mathrm{G}_kd_k=-\mathrm{g}_k\)
  4. 令 \(\mathrm{x}_{k+1}=\mathrm{x}_k+\mathrm{d}_k\)，同时 \(k=k+1\)，回到第二步。

逆矩求法 \[ \begin{bmatrix} a&b\\ c&d \end{bmatrix}^{-1}=\frac{1}{ad-bc}\begin{bmatrix} d&-b\\ -c&a \end{bmatrix} \]

当初始点远离极小点时，牛顿法可能不收敛。

阻尼牛顿法

在牛顿法的基础上，增加了沿牛顿方向的线搜索，迭代公式变为 \[ \mathrm{x}_{k+1}=\mathrm{x}_k+\alpha_k\mathrm{d}_k \] 其中，\(\mathrm{d}_k=-\nabla^2f(\mathrm{x}_k)^{-1}\nabla f(\mathrm{x}_k)\)。

牛顿法与梯度下降的比较

  1. 牛顿法是二阶收敛，梯度下降是一阶收敛，所以显然牛顿法收敛速度会更快。
  2. 从几何上来说，牛顿法就是用一个二次曲面去拟合当前所处位置的局部曲面，而梯度下降是用一个平面去拟合当前的局部曲面，通常情况下二次曲面拟合度更优。
  3. 牛顿法收敛速度相比梯度下降法常常较快，但计算开销大。
  4. 牛顿法对初始值有一定要求，在非凸优化问题中（如神经网络训练），牛顿法很容易陷入鞍点（牛顿法步长会越来越小），而梯度下降法很容易逃离鞍点（因此在神经网络训练中一般使用梯度下降法，高维空间的神经网络中存在大量鞍点）。
  5. 梯度下降法在靠近最优点时会震荡，因此步长调整在梯度下降法中是必要的，具体有 adagrad, adadelta, rmsprop, adam 等一系列自适应学习率的算法。

非线性最小二乘法

非线性最小二乘问题是求向量 \(\mathrm{x}\in R^n\) 使得 \(\|F(\mathrm{x})\|^2\) 最小。

记 \(F(\mathrm{x})=[F_1(\mathrm{x}),\cdots,F_m(\mathrm{x})]^T\)，问题一般写作 \[ \min_{\mathrm{x}\in R^n} f(\mathrm{x})=\frac{1}{2}\|F(\mathrm{x})\|^2=\frac{1}{2}\sum^m_{i=1}F_i^2(\mathrm{x}) \] 对函数计算梯度和二阶梯度 \[ g(\mathrm{x})=\nabla f(\mathrm{x})=J(\mathrm{x})^TF(\mathrm{x})=\sum^m_{i=1}F_i(\mathrm{x})\nabla F_i(\mathrm{x})\newline G(\mathrm{x})=\nabla^2f(\mathrm{x})=J(\mathrm{x})^TJ(\mathrm{x})+S(\mathrm{x}) \] 其中， \[ J(\mathrm{x})=F'(\mathrm{x})=[\nabla F_1(\mathrm{x}),\cdots,\nabla F_m(\mathrm{x})]^T\newline S(\mathrm{x})=\sum^m_{i=1}F_i(\mathrm{x})\nabla^2F_i(\mathrm{x}) \] 根据牛顿法，我们可以写出求解非线性最小二乘问题的迭代公式 \[ \mathrm{x}_{k+1}=\mathrm{x}_k-(J_k^TJ_k+S_k)^{-1}J_k^TF(\mathrm{x}_k) \] 但是考虑到 \(S_k\) 计算量较大，所以忽略这一项，这样就得到了求解非线性最小二乘法的高斯牛顿迭代算法 \[ \mathrm{x}_{k+1}=\mathrm{x}_k+\mathrm{d}_k^{GN} \] 其中， \[ \mathrm{d}_k^{GN}=-(J_k^TJ_k)^{-1}J_k^TF(\mathrm{x}_k) \] 容易验证 \(\mathrm{d}_k^{GN}\) 是优化问题 \[ \min_{\mathrm{d}\in R^n}\frac{1}{2}\|F(\mathrm{x}_k)+J_k\mathrm{d}\|^2 \] 的最优解。

若向量函数 \(F(\mathrm{x})\) 的雅可比矩阵是列满秩的，则可以保证方向是下降方向。

优点：

  1. 对于零残量问题，即 \(f(\mathrm{x}^*)=0\)，有局部二阶收敛速度。
  2. 对于小残量问题，即 \(f(\mathrm{x})\) 较小，或接近于线性，有快的局部收敛速度。
  3. 对于线性最小二乘问题，一步达到极小点。

缺点：

  1. 对于不是很严重的大残量问题，有较慢的收敛速度。
  2. 对于残量很大的问题或者 \(f(\mathrm{x})\) 的非线性程度很大的问题，不收敛。
  3. 如果 \(A(\mathrm{x}_k)\) 不满秩，方法没有定义。
  4. 不一定总体收敛。