模式识别-线性判别函数笔记

发表于 更新于 本文字数： 23k 阅读时长 ≈ 21 分钟
有关线性判别函数的简要笔记

模式识别

二类线性判别函数

线性判别函数有许多优势，其中一个优势是便于分析和计算。在之前的贝叶斯决策中笔记中曾简单涉及到的贝叶斯判别函数，当满足某些情况时，判别函数是线性的。

我们抽象出这种线性特质，即定义线性判别函数形如 \[ g(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+w_0 \] 其中，\(\boldsymbol{w}\) 是权向量（weight vector），决定了特征向量中每个属性在判别函数中的占比；\(w_0\) 是偏置（bias），决定了该线性判别函数的位置。

在这其中，二类线性判别函数在实战中常被用到，故以下仅讨论二类线性判别函数的问题，其中可能往往都以二维二类线性判别函数为例。

性质一：权向量 \(\boldsymbol{w}\) 与判别面上任意一个向量正交，即权向量决定了判别边界的方向。

对于一个二维二类线性判别函数，假设判别面上存在任意两点 \(x_1,x_2\)，那么其满足 \[ \boldsymbol{w}^Tx_1+w_0=\boldsymbol{w}^Tx_2+w_0 \] 可以改写成 \[ \boldsymbol{w}^T(x_1-x_2)=0 \] 即权向量与判别面上的任意一向量正交（相互垂直）。

可以推广到，权向量同时也与超平面（多维情况下的判别边界）上的任意向量正交。

性质二：判别函数 \(g(\boldsymbol{x})\) 与特征向量 \(\boldsymbol{x}\) 到判决边界（判决面）的距离成正比。

我们定义 \(r\) 为特征空间中某点 \(\boldsymbol{x}\) 到判决边界（超平面）的算数距离（正代表在超平面正侧，反之亦然）；使用 \(\frac{\boldsymbol{w}}{\|\boldsymbol{w}\|}\) 来表示单位向量，那么特征向量 \(\boldsymbol{x}\) 可以表示成 \[ \boldsymbol{x}=\boldsymbol{x}_p+r\frac{\boldsymbol{w}}{\|\boldsymbol{w}\|} \] 其中 \(\boldsymbol{x}_p\) 是特征向量在判决边界上的投影，有 \(g(\boldsymbol{x}_p)=0\)。

代入判决函数，可以得到 \[ \boldsymbol{w}^T\boldsymbol{x}+w_0=r\|\boldsymbol{w}\| \] 即 \[ r=\frac{g(\boldsymbol{x})}{\|\boldsymbol{w}\|} \]

由性质二，我们定义

\(g(\boldsymbol{x})>0\) 称作判决边界（判决面）的正面；\(g(\boldsymbol{x})<0\) 称作判决边界的反面；\(g(\boldsymbol{x})=0\) 则 \(\boldsymbol{x}\) 是在判决边界上。

性质三：线性判别函数中的偏置 \(w_0\) 表征了原点到判别边界的距离。若 \(w_0>0\)，则原点位于判别边界的正面；反之亦然。

我们显然可以得知 \[ g(\boldsymbol{0})=w_0 \] 故结论显然。

多类情况下的线性判别函数

情况一

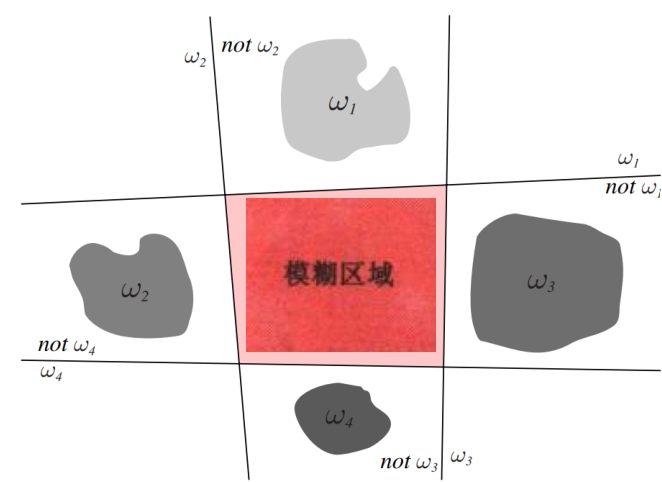
如果每个模式类均可用一个单独的线性判别边界与其余模式类分开，那么此时仅需 \(c\) 个判别函数，且具有以下性质： \[ \begin{cases} g_i(\boldsymbol{x})>0 & \boldsymbol{x}\in\omega_i\\ g_i(\boldsymbol{x})<0 & \boldsymbol{x}\notin\omega_i \end{cases} \] 情况一下的多类问题分类界面

当关于特征向量有 \(\boldsymbol{x}\) 满足 \(g_i(\boldsymbol{x})>0\) 且所有 \(g_j{(\boldsymbol{x})}<0\) 时，判决为 \(\omega_i\)；反之不作判决。

故可以发现，该方法存在失效区或不定区，在图中表现为模糊区域，即存在多于一个判别函数大于 0 或所有的判别函数都小于 0。

情况二

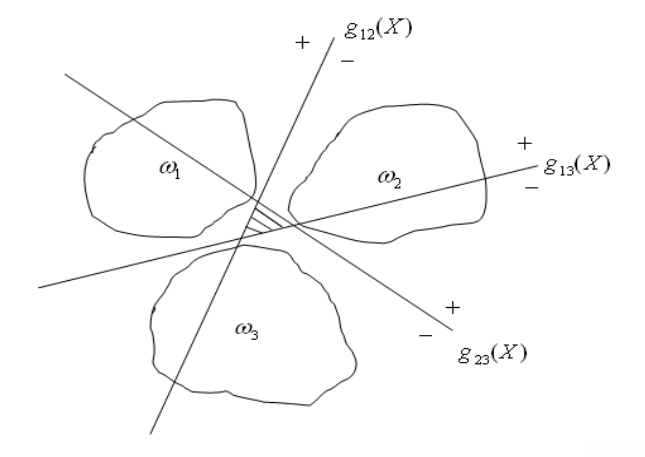
如果线性判别边界只能将模式类两两分开，那么需要 \(c(c-1)/2\) 个判别函数，且具有以下性质 \[ \begin{cases} g_{ij}(\boldsymbol{x})>0 & \boldsymbol{x}\in\omega_i\\ g_{ij}(\boldsymbol{x})<0 & \boldsymbol{x}\in\omega_j \end{cases} \] 显然，应有 \[ g_{ij}(\boldsymbol{x})=-g_{ji}(\boldsymbol{x}) \] 情况二下的多类问题分类界面

当特征向量 \(\boldsymbol{x}\) 满足对所有的 \(j\neq i\) 均有 \(g_{ij}(\boldsymbol{x})>0\)，那么判决为 \(\omega_i\)，反之不判决。

同理，该种方式任然存在不定区，采用拒识策略。

拒识策略即不进行判决。

情况三

不考虑二类问题的线性判别函数，采用 \(c\) 个线性判别函数进行分类，但不同于情况一，此时的识别准则变更为

对于所有的 \(i\neq j\)，若 \(g_i(\boldsymbol{x})>g_j(\boldsymbol{x})\)，则判决为 \(\omega_i\)。

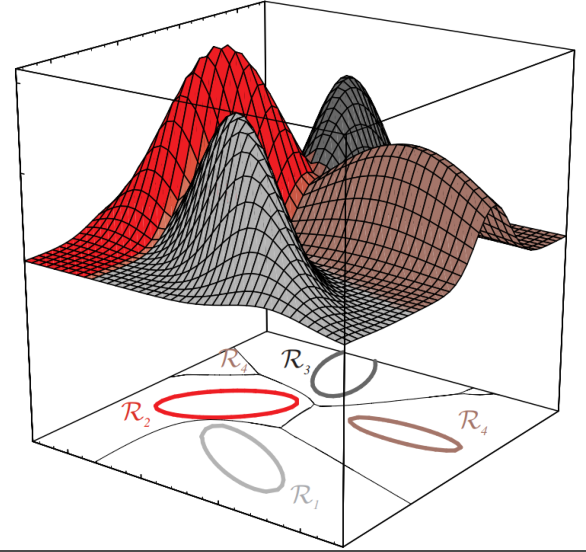
该种方法实际上是将特征空间划分为 \(c\) 个判决区域 \(\{R_1,R_2,\cdots,R_c\}\)，在判决区域 \(R_i\) 内，\(g_i(\boldsymbol{x})\) 具有最大的函数值。

如果 \(R_i\) 与 \(R_j\) 相邻，则决策面是方程 \(g_i(\boldsymbol{x})=g_j(\boldsymbol{x})\) 的一部分。

因为决策面还有可能与其他模式冲突，所以这里描述为一部分。

但该种方法的优点是不存在不定区。

情况三下的多类问题分类界面

总结

由上述情况可知，多类情况实际上可以转化为二类问题进行处理，故我们仅需研究二类问题中的线性判别函数即可。

线性判别函数的学习算法

增广化

我们知道线性判别函数一般具有以下形式 \[ g(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+w_0=w_1x_1+w_2x_2+\cdots+w_dx_d+w_0 \] 不妨我们设 \[ \boldsymbol{a}=\begin{bmatrix} w_0\\ w_1\\ \vdots\\ w_d \end{bmatrix},\boldsymbol{y}=\begin{bmatrix} 1\\ x_1\\ \vdots\\ x_d \end{bmatrix} \] 将原判别函数写成 \[ g(\boldsymbol{y})=\boldsymbol{a}^T\boldsymbol{y} \] 其中 \(\boldsymbol{a},\boldsymbol{y}\) 的维度均为 \(d+1\) 维。

我们把这种化简称作增广化。

比如说我们有两类样本 \[ \omega_1:\boldsymbol{x}_{11}=(0,0),\boldsymbol{x}_{12}=(0,1)\\ \omega_2:\boldsymbol{x}_{21}=(1,0),\boldsymbol{x}_{22}=(1,1)\\ \] 我们对其进行增广化，得到 \[ \omega_1:\boldsymbol{x}_{11}=(1,0,0),\boldsymbol{x}_{12}=(1,0,1)\\ \omega_2:\boldsymbol{x}_{21}=(1,1,0),\boldsymbol{x}_{22}=(1,1,1)\\ \]

增广化的结果不唯一，比如说也可以存在增广化结果为 \(\boldsymbol{x}_{11}=(0,0,1)\)

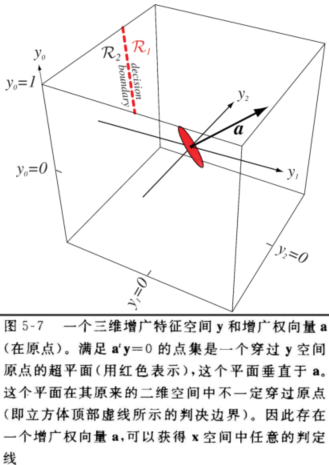
增广化后的线性判别函数，判别面是过原点的超平面。

对于过原点的一个判决边界，简化了我们计算权向量的过程。

同时对于二类问题，有

若 \(g(\boldsymbol{y})=\boldsymbol{a}^T\boldsymbol{y}>0\)，则 \(\boldsymbol{y}\in\omega_1\)，即 \(\boldsymbol{x}\in\omega_1\)；

若 \(g(\boldsymbol{y})=\boldsymbol{a}^T\boldsymbol{y}<0\)，则 \(\boldsymbol{y}\in\omega_2\)，即 \(\boldsymbol{x}\in\omega_2\)。

一个三维增广化后的特征空间

规范化

沿着上面的增广化，比如说对于一个一维二类线性判别函数，它增广化后的判决面（二维空间）是权空间中的一条直线，这条直线将不同类别的向量区分开。

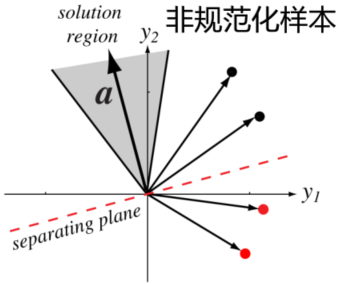
非规范化样本

于是乎我们可以得到在某个范围内的权向量 \(\boldsymbol{a}\) 构造出的直线都能满足这个条件，我们称这个区域叫做解区域（solution region）。

但在计算上，验证某些向量是否被这条直线错误的区别是繁琐的，但学习过程中却又需要大量验证某些向量是否被错误分类了，故我们需要对这些向量进行规范化。

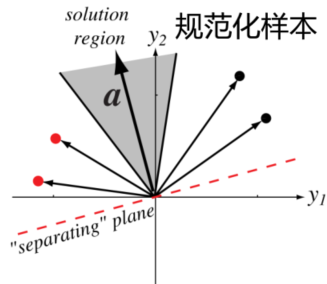
我们不妨令对于所有 \(\boldsymbol{y}\in \omega_2\) 都有 \[ \boldsymbol{y}=-\boldsymbol{y} \] 这样，我们就使得所有的正确分类都有 \[ g(\boldsymbol{y})>0 \] 规范化样本

当我们需要判断某个向量是否被权向量错误分类时，仅需有如下规则：

若 \(g(\boldsymbol{y})>0\)，则 \(\boldsymbol{y}\) 被正确分类；

若 \(g(\boldsymbol{y})<0\)，则 \(\boldsymbol{y}\) 被错误分类。

这极大的简化了运算过程。

跟随上文，我们有如下被增广化后的向量 \[ \omega_1:\boldsymbol{x}_{11}=(1,0,0),\boldsymbol{x}_{12}=(1,0,1)\\ \omega_2:\boldsymbol{x}_{21}=(1,1,0),\boldsymbol{x}_{22}=(1,1,1)\\ \] 对其进行规范化，有 \[ \begin{align} &\omega_1:\boldsymbol{x}_{11}=(1,0,0),\boldsymbol{x}_{12}=(1,0,1)\\ &\omega_2:\boldsymbol{x}_{21}=(-1,-1,0),\boldsymbol{x}_{22}=(-1,-1,-1) \end{align} \] 对于满足所有上述条件的向量 \(\boldsymbol{a}\) 都称作是解向量，也可以发现，每个学习样本都对解向量做了限制，但解向量也不唯一。

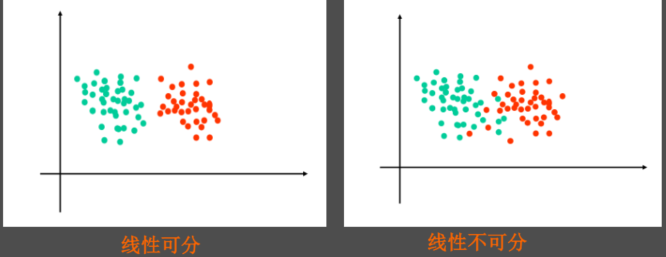
如果存在解向量 \(\boldsymbol{a}\) 使得二类样本分类正确，则样本被称作是线性可分的；反之称作线性不可分。

线性可分

学习算法原理

要求解解向量 \(\boldsymbol{a}\)，根据上面的理论我们需要通过学习样本来求解不等式组 \[ \boldsymbol{a}^T\boldsymbol{y}_i>0,i=1,2,\cdots,n \] 但当权向量维度很大，学习样本足够多时，显然直接求解不等式组是困难的。

同时我们希望在样本线性可分时，得到的判别函数能够将所有的训练样本正确分类；在样本线性不可分时，得到的判别函数产生错误的概率最小（或者称误差最小）。

为转化困难问题为简单问题，我们定义一个标量函数 \(J(\boldsymbol{a})\)，如果 \(J(\boldsymbol{a})\) 的值越小，则判别面的分割质量越高。

标量函数指的是输出值为标量的函数，同时有时也称准则函数。

那么求解解向量 \(\boldsymbol{a}\) 就变为求解标量函数 \(J(\boldsymbol{a})\) 极小值（最小值）的问题。

那么如何定义合理的标量函数 \(J(\boldsymbol{a})\) 能更准确的表示它的含义成为了新问题。

最直观的准则函数的定义是最少错分样本数准则，即令 \(J(\boldsymbol{a})\) 为样本集合中被错误分类的样本数。

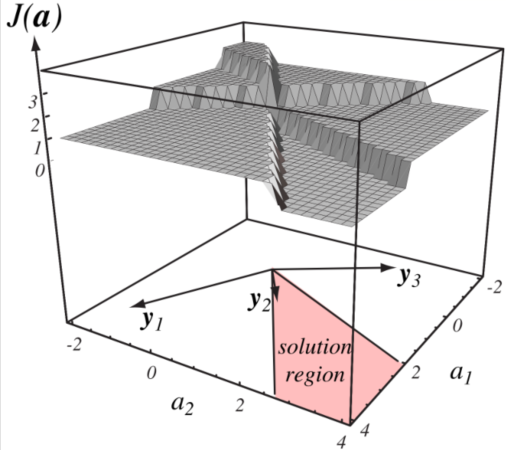
最少错分样本数准则下的准则函数

但我们可以直观的发现，此时 \(J(\boldsymbol{a})\) 是一个分段函数，对于这种函数在性质上是不被喜欢的，因为它不光滑，无法用现有的高效的数学工具求解函数极小值，对计算机来说可能将要遍历所有的函数值才能找到它的极小值。

因此，一个更好的选择是错分样本到判别面的距离之和准则，也称作感知器准则，感知器准则函数的定义如下 \[ J_p(\boldsymbol{a})=\sum_{\boldsymbol{y}\in Y_e}(-\boldsymbol{a}^T\boldsymbol{y}) \] 即选择了某个解向量 \(\boldsymbol{a}\) 后，被错分的样本到判别面的距离之和，其中 \(Y_e\) 代表所有被错分向量的集合。

这里的计算是规范化后的计算，所以需要加个负号，这样仅需关注距离和。

此时满足 \(J_p(\boldsymbol{a})\geq 0\)，其存在极小值使得样本无错分或错分误差最小。

当且仅当样本线性可分时，极小值取得 0。

梯度下降算法

梯度下降算法是一个用来求函数极小值的算法，仅需要知道函数在各点的导数，便可以快速迭代找到极小值点。

需要注意的是，梯度下降算法仅适用于局部连续可导函数。

原理

对于某一个局部连续可导函数 \(f(x)\)。

  1. （随机）选取一个初始值 \(x_0\)；
  2. 计算 \(f'(x_0)\)，如果值为负则增加 \(x_0\)；如果值为正则减小 \(x_0\)；
  3. 使 \(x_1=x_0-\eta f'(x_0)\)，代入 \(x_1\) 重复第二步，直到 \(|\eta f'(x_{n-1})|<\theta\)，\(\theta\) 为临界值（误差值）。

我们也称 \(\eta\) 为学习率。

如果对于多参函数，例如二元函数 \(f(x,y)\)，我们选择以某一点的梯度来增长或减小。

因为我们是想让值快速迭代到极小值点处，而梯度是多元函数增长速度最快的方向，则负梯度是多元函数下降速度最快的方向。需要知道，\(\|\nabla J(\boldsymbol{a})\|\) 表示其在 \(\boldsymbol{a}\) 处的变化率的大小，当某点梯度为 \(\boldsymbol{0}\) 时，该点即为 \(J(\boldsymbol{a})\) 的极值点。

即第三步的式子变为 \[ x_n=x_{n-1}-\eta\nabla f(x_{n-1}, y_{n-1})\\ y_n=y_{n-1}-\eta\nabla f(x_{n-1}, y_{n-1}) \] 其中 \[ \nabla f(x_{n-1},y_{n-1})=\begin{bmatrix} \frac{\partial}{\partial x}f(x_{n-1},y_{n-1})\\ \frac{\partial}{\partial y}f(x_{n-1},y_{n-1}) \end{bmatrix} \] 同理如果对于 \(J(\boldsymbol{a})\)，有 \[ \nabla J(\boldsymbol{a})=\begin{bmatrix} \frac{\partial}{\partial a_1}\\ \frac{\partial}{\partial a_2}\\ \vdots\\ \frac{\partial}{\partial a_{d+1}}\\ \end{bmatrix}J(\boldsymbol{a}) \] 由于其通过梯度快速下降，故称作梯度下降法。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def f(x):
    return x * x + 2 * x

def df(x):
    return 2 * x + 2

def gradient_descent(df, init_val = 1, learning_rate = 0.01, precision = 1e-5):
    """
    Using Gradient Descent to get local minimum

    `Parameter`:
        df - Derivative
        init_val - Initial value
        learning_rate - Learning rate
        precision - Precision

    `Return`
        Local minimun
    """
    x = init_val
    xs = [x]
    while True:
        x = x - learning_rate * df(x)
        xs.append(x)
        if abs(learning_rate * df(x)) < precision:
            break
    print("Cost %d times calculation." % len(xs))
    return x

print(gradient_descent(df))
"""
Cost 412 times calculation.
-0.9995046101486759
"""

优劣

如果 \(\eta\) 过大可能会导致过冲（overshoot）甚至发散，即在极小值两边迭代无法退出循环；\(\eta\) 过小会导致迭代次数过多，浪费算力。所以一般会选择较小但不是特别小的 \(\eta\) 进行梯度下降。

牛顿下降法

基于梯度下降算法和牛顿迭代法进行改进，得到牛顿下降法。

原理

  1. （随机）选取一个初始值 \(\boldsymbol{x}_0\)；
  2. 计算 \(\nabla f(\boldsymbol{x}_0)\) 和 \(\boldsymbol{H}^{-1}\)；
  3. 使 \(\boldsymbol{x}_1=\boldsymbol{x}_0-\boldsymbol{H}^{-1}\nabla f(\boldsymbol{x}_0)\)，代入 \(x_1\) 重复第二步，直到 \(|\boldsymbol{H}^{-1}\nabla f(\boldsymbol{x}_{n-1})|<\theta\)，\(\theta\) 为临界值（误差值）。

其中 \(H\) 为海森矩阵。

优劣

牛顿下降法可以更快更准确的进行下降，但反过来计算 \(H\) 的逆矩阵是困难的，所以一般并不会使用牛顿下降法，而是会选择小 \(\eta\) 的梯度下降法。

感知器梯度下降法

在了解了梯度下降算法后，我们回到判别函数 \(g(\boldsymbol{y})\) 的感知器准则函数 \(J_p(\boldsymbol{a})\)。

我们由原式可得，感知器准则函数的梯度为 \[ \nabla J_p=\sum_{\boldsymbol{y}\in Y_e}(-\boldsymbol{y}) \] 那么我们就可以把梯度下降的公式改写为 \[ \boldsymbol{a}_{n+1}=\boldsymbol{a}_{n}+\eta(n)\sum_{\boldsymbol{y}\in Y_e}\boldsymbol{y} \] 结束条件直到 \(|\eta(n)\sum_{\boldsymbol{y}\in Y_e}\boldsymbol{y}|<\theta\)。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
import numpy as np
from matplotlib import pyplot as plt

# Sample
omega1 = [(4, 28), (7, 23), (16, 27), (18, 30), (2, 17), (13, 24), (2, 24), (12, 29), (2, 21), (5, 26), (2, 24), (11, 18), (8, 28), (3, 21), (13, 22)]
omega2 = [(14, 12), (25, 28), (8, 7), (26, 29), (29, 23), (18, 1), (19, 12), (19, 25), (23, 17), (30, 2), (18, 22), (28, 17), (24, 20), (9, 4), (25, 14)]
omega1 = np.array(omega1)
omega2 = np.array(omega2)

# Plot
x = omega1[:, 0]
y = omega1[:, 1]
plt.scatter(x, y, s=20, c='red', marker='s')
x = omega2[:, 0]
y = omega2[:, 1]
plt.scatter(x, y, s=20, c='green', marker='s')

# Augmented Vector
omega1 = np.hstack((omega1, np.ones((len(omega1), 1))))
omega2 = np.hstack((omega2, np.ones((len(omega1), 1))))

# Normalization
omega2 = -omega2
samples = np.vstack([omega1, omega2])
sample_number = len(samples)

# Laerning Rate
eta = 0.01

# Criterion Function
def Jp(a, ys):
    rst = 0
    for y in ys:
        if np.dot(a, y) < 0:
            rst += -np.dot(a, y)
    return rst

# Gradient of Criterion Function
def nablaJp(a, ys):
    rst = np.zeros(ys.shape[1])
    for y in ys:
        if np.dot(a, y) < 0:
            rst += -y
    return rst

# Perceptron Gradient Descent
def perceptron(samples, eta, theta = 0.001):
    count = 0
    a = np.ones(samples.shape[1])
    while True:
        nabla = nablaJp(a, samples)
        if np.linalg.norm(eta * nabla) < theta:
            break
        a = a - eta * nabla
        count += 1
    print("Perceptron cost %d times iterate." % count)
    return a

# Solve Weight Vector
a = perceptron(samples, eta)

# Turn to Feature Space
xs = []
ys = []
xs += [0, 20]
ys += [(xs[0] * a[0] + a[2]) / -a[1], (xs[1] * a[0] + a[2]) / -a[1]]

# Plot Judgment Boundary
plt.plot(xs, ys)
print(Jp(a, samples))
"""
Perceptron cost 7 times iterate.
0
"""

对于这组样本，仅需 7 次迭代即求得解向量。

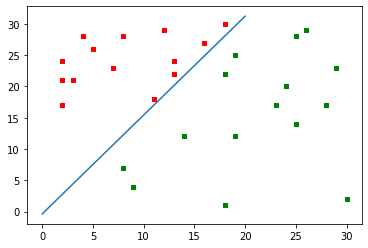
二维二类权空间的感知器梯度下降

固定增量法

感知器梯度下降法需要一次获取所有学习样本，并在迭代算法中一次遍历所有样本。

但实际应用中，有时样本是分批获取的，先训练一部分样本，再训练一部分样本。

固定增量法就是根据以上需求改变的感知器算法，基本思想是每次修改解向量时，不遍历所有样本，而是将学习样本串行输入，每考察一个样本就对解向量 \(a\) 进行一次修改。

即迭代公式为 \[ \boldsymbol{a}_{n+1}=\boldsymbol{a}_{n}+\eta(n)\boldsymbol{y},\boldsymbol{y}\in Y_e \] 结束条件直到 \(|\boldsymbol{a}_{n+1}-\boldsymbol{a}_{n}|<\theta\)。

这样做到了每当解向量分类错误时，就修改解向量，在算法时间复杂度不变的情况下，提升了解向量迭代的效率。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import numpy as np
from matplotlib import pyplot as plt

# Sample
omega1 = [(4, 28), (7, 23), (16, 27), (18, 30), (2, 17), (13, 24), (2, 24), (12, 29), (2, 21), (5, 26), (2, 24), (11, 18), (8, 28), (3, 21), (13, 22)]
omega2 = [(14, 12), (25, 28), (8, 7), (26, 29), (29, 23), (18, 1), (19, 12), (19, 25), (23, 17), (30, 2), (18, 22), (28, 17), (24, 20), (9, 4), (25, 14)]
omega1 = np.array(omega1)
omega2 = np.array(omega2)

# Plot
x = omega1[:, 0]
y = omega1[:, 1]
plt.scatter(x, y, s=20, c='red', marker='s')
x = omega2[:, 0]
y = omega2[:, 1]
plt.scatter(x, y, s=20, c='green', marker='s')

# Augmented Vector
omega1 = np.hstack((omega1, np.ones((len(omega1), 1))))
omega2 = np.hstack((omega2, np.ones((len(omega1), 1))))

# Normalization
omega2 = -omega2
samples = np.vstack([omega1, omega2])
sample_number = len(samples)

# Laerning Rate
eta = 0.01

# Criterion Function
def Jp(a, ys):
    rst = 0
    for y in ys:
        if np.dot(a, y) < 0:
            rst += -np.dot(a, y)
    return rst

# Perceptron Gradient Descent
def perceptron(samples, eta, theta = 0.001):
    count = 0
    a = np.ones(samples.shape[1])
    while True:
        ap = a
        for y in samples:
            if np.dot(a, y) < 0:
                a = a + eta * y
        count += 1
        if np.linalg.norm(a - ap) < theta:
            break
    print("Perceptron cost %d times iterate." % count)
    return a

# Solve Weight Vector
a = perceptron(samples, eta)

# Turn to Feature Space
xs = []
ys = []
xs += [0, 20]
ys += [(xs[0] * a[0] + a[2]) / -a[1], (xs[1] * a[0] + a[2]) / -a[1]]

# Plot Judgment Boundary
plt.plot(xs, ys)
print(Jp(a, samples))
"""
Perceptron cost 5 times iterate.
0
"""

对于这组样本，仅需 5 次迭代即求得解向量。

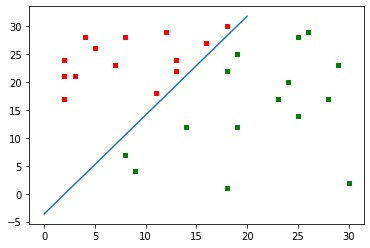
二维二类权空间的固定增量法

当样本数量增多时，固定增量法的效率优化会更明显。

但固定增量法需要样本满足二类可分条件，否则无法退出迭代。

感知器算法收敛定理：如果训练样本是线性可分的，固定增量法给出的权向量序列必定终止于某个解向量。

变增量梯度算法

单一的 \(\eta\) 会导致效率一定，这个时候就会想使得 \(\eta\) 会随着迭代次数的增加而变化，即 \[ \eta\to\eta(n) \] 我们可以证明得到，当对于所有 \(n\) 有 \[ \eta(n)\geq 0\\ \lim_{m\to\infty}\sum^m_{n=1}\eta(n)=\infty\\ \lim_{m\to\infty}\frac{\sum^m_{n=1}\eta^2(n)}{(\sum^m_{n=1}\eta(n))^2}=0 \] 即正项级数 \(\eta(n)\) 发散，但满足一定条件，那么我们可以证明其迭代算法 \[ \boldsymbol{a}_{n+1}=\boldsymbol{a}_{n}+\eta(n)\boldsymbol{y} \] 是一定收敛的。

这也就是为什么在之前的公式中的学习率都以 \(\eta(n)\) 表示。

带裕量的感知器算法

我们知道，解向量可以有无数多种，解区域也是有边界的，有的时候我们并不想让结果解向量太靠近边界，这样会使得分类严格。

根据固定增量法进行改进，我们加入裕量（margin）来均衡解向量的结果，使得迭代算法变为：

当 \(\boldsymbol{a}^T\boldsymbol{y}_i\leq b\) 时，我们就修改解向量 \[ \boldsymbol{a}_{n+1}=\boldsymbol{a}_{n}+\eta(n)\boldsymbol{y} \]

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import numpy as np
from matplotlib import pyplot as plt

# Sample
omega1 = [(4, 28), (7, 23), (16, 27), (18, 30), (2, 17), (13, 24), (2, 24), (12, 29), (2, 21), (5, 26), (2, 24), (11, 18), (8, 28), (3, 21), (13, 22)]
omega2 = [(14, 12), (25, 28), (8, 7), (26, 29), (29, 23), (18, 1), (19, 12), (19, 25), (23, 17), (30, 2), (18, 22), (28, 17), (24, 20), (9, 4), (25, 14)]
omega1 = np.array(omega1)
omega2 = np.array(omega2)

# Plot
x = omega1[:, 0]
y = omega1[:, 1]
plt.scatter(x, y, s=20, c='red', marker='s')
x = omega2[:, 0]
y = omega2[:, 1]
plt.scatter(x, y, s=20, c='green', marker='s')

# Augmented Vector
omega1 = np.hstack((omega1, np.ones((len(omega1), 1))))
omega2 = np.hstack((omega2, np.ones((len(omega1), 1))))

# Normalization
omega2 = -omega2
samples = np.vstack([omega1, omega2])
sample_number = len(samples)

# Laerning Rate
eta = 0.01

# Criterion Function
def Jp(a, ys):
    rst = 0
    for y in ys:
        if np.dot(a, y) < 0:
            rst += -np.dot(a, y)
    return rst

# Perceptron Gradient Descent
def perceptron(samples, eta, theta = 0.001, b = 0):
    count = 0
    a = np.ones(samples.shape[1])
    while True:
        ap = a
        for y in samples:
            if np.dot(a, y) < b:
                a = a + eta * y
        count += 1
        if np.linalg.norm(a - ap) < theta:
            break
    print("Perceptron cost %d times iterate." % count)
    return a

# Solve Weight Vector
a = perceptron(samples, eta, b = 1)

# Turn to Feature Space
xs = []
ys = []
xs += [0, 20]
ys += [(xs[0] * a[0] + a[2]) / -a[1], (xs[1] * a[0] + a[2]) / -a[1]]

# Plot Judgment Boundary
plt.plot(xs, ys)
print(Jp(a, samples))
"""
Perceptron cost 7 times iterate.
0
"""

对于这组样本，需 7 次迭代求得解向量。

不难看出，带裕量的感知器算法会使得迭代次数变多，但这是可以控制的，远低于原始的感知器梯度下降法的迭代次数。

同时我们通过添加裕量 \(b=1\)，使得判决边界更加趋近于解空间的中间。

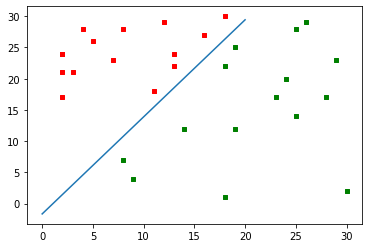
二维二类权空间的带裕量的固定增量法

Fisher 线性判别

原理

我们知道上面线性判别的方式是增加维度的，这样可以精确的描述一个线性判别函数；同时特征空间的纬度越高，判别的精确度就越高。

但这与此同时也带来一个灾难性的问题，就是高纬度的计算总是复杂和苦难的，因此 Fisher 研究的是降维领域。

由判别函数的式子可知 \[ g(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x} \] 可以理解为特征向量在权向量上的投影，如果说我们对所有的特征向量都做一次投影，应该是下图所示

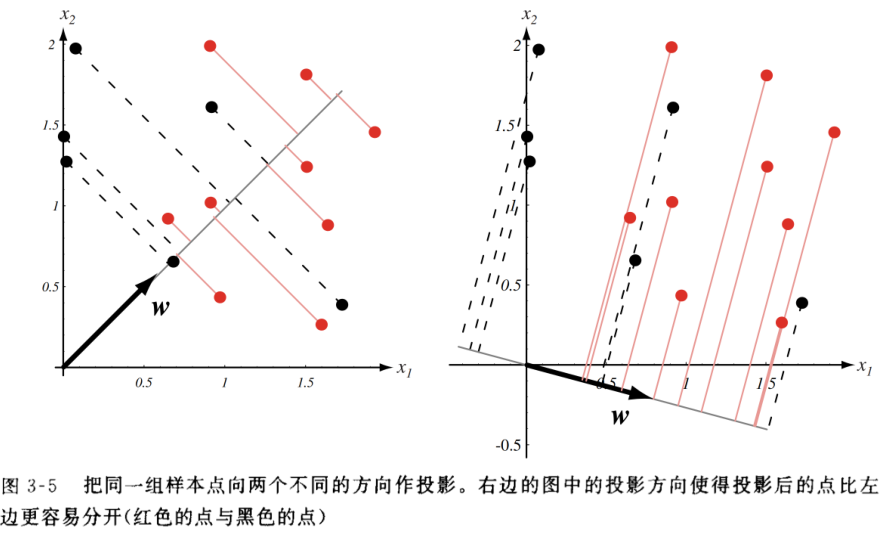
各向量对权向量的投影

可以很自然的发现，我们将二维的权空间转化到了一维上，此时我们只考虑投影值的大小，而非特征向量的空间分布。

如果说把其转化为一维可视图像，正如图所示

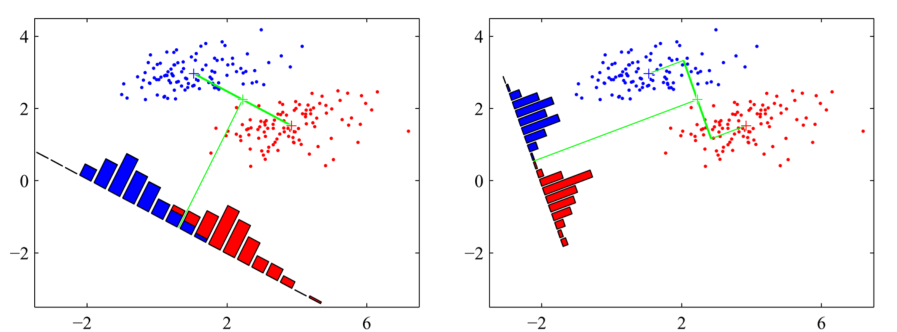
Fisher准则一维化

很显然，我们发现不同的权向量会导致一维图像上有不同的结果，左图的权向量显然错分数更多，映射到一维图像上就是有所重合；有图的权向量显然错分数更少，映射到一维图像上就是类间数据有所分离。

自然的，我们会认为，最好的分类是将类间数据进行分离，而类内数据进行聚合，使得两类分离，这就是 Fisher 判别准则。

LDA 基本原理：投影后具有最佳可分离性，即最大的类间距离和最小的类内距离。

我们定义类内距离以投影均值表示，类间距离以投影方差表示，那么想要同时优化两个目标，即想让样本均值之差大，样本方差尽量小，那么定义准则函数 \[ J(\boldsymbol{w})=\frac{|\tilde{m}_1-\tilde{m}_2|}{\tilde{s}_1^2+\tilde{s}_2^2} \] 那么有样本均值 \[ \boldsymbol{m}_i=\frac{1}{n_i}\sum\boldsymbol{x} \] 推导可得 \[ \begin{align} \tilde{m}_i&=\frac{1}{n_i}\sum g(\boldsymbol{x})\\ &=g(\boldsymbol{m}_i) \end{align} \] 同时 \[ \begin{align} \tilde{s}_i^2&=\sum(g(\boldsymbol{x})-\tilde{m}_i)\\ &=\sum\boldsymbol{w}^T(\boldsymbol{x}-\boldsymbol{m}_i)(\boldsymbol{x}-\boldsymbol{m}_i)^T\boldsymbol{w}\\ &=\boldsymbol{w}^T\boldsymbol{S}_i\boldsymbol{w} \end{align} \] 那么总的就有 \[ \begin{align} \tilde{s}_1^2+\tilde{s}_2^2&=\boldsymbol{w}^T(\boldsymbol{S}_1+\boldsymbol{S}_2)\boldsymbol{w}\\ &=\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}\\ (\tilde{m}_1-\tilde{m}_2)^2&=\boldsymbol{w}^T(\boldsymbol{m}_1-\boldsymbol{m}_2)(\boldsymbol{m}_1-\boldsymbol{m}_2)^T\boldsymbol{w}\\ &=\boldsymbol{w}^T\boldsymbol{S}_B\boldsymbol{w} \end{align} \] 那么准则函数变为 \[ J(\boldsymbol{w})=\frac{\boldsymbol{w}^T\boldsymbol{S}_B\boldsymbol{w}}{\boldsymbol{w}^T\boldsymbol{S}_W\boldsymbol{w}} \] 我们想要找到的是这个准则函数的最大值，那么此时需要找到该函数的导数为零点。

可以最终计算得到 \[ J'(\boldsymbol{w})=0\Rightarrow \boldsymbol{w}=\boldsymbol{S}_W^{-1}(\boldsymbol{m}_1-\boldsymbol{m}_2) \]

示例

现有某商品评分表如下

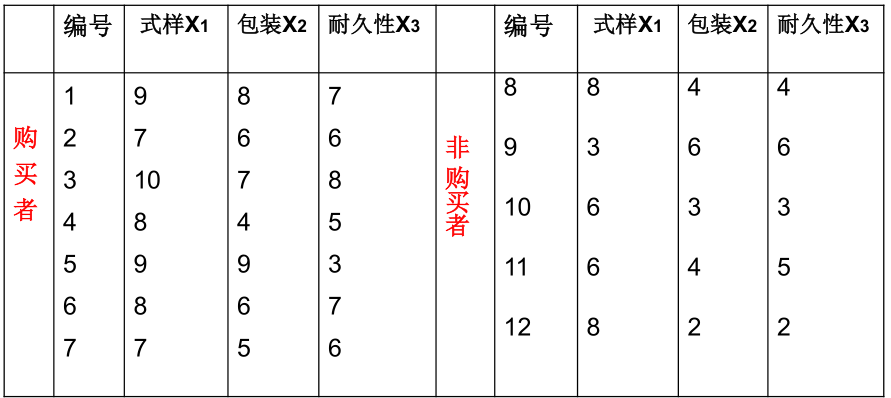
fisher准则示例图标

现在有评分为 \(\boldsymbol{x}^T=(9, 5, 4)\)，判断其是否愿意购买此商品。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import numpy as np
from matplotlib import pyplot as plt

# Sample
omega1 = [(9, 8, 7), (7, 6, 6), (10, 7, 8), (8, 4, 5), (9, 9, 3), (8, 6, 7), (7, 5, 6)]
omega2 = [(8, 4, 4), (3, 6, 6), (6, 3, 3), (6, 4, 5), (8, 2, 2)]
omega1 = np.array(omega1)
omega2 = np.array(omega2)

# Get Average
m1 = np.average(omega1, axis=0)
m2 = np.average(omega2, axis=0)

# Calculate S_i
A = omega1 - m1
B = omega2 - m2

S1 = np.dot(A.T, A)
S2 = np.dot(B.T, B)

# Calculate S_W
S = S1 + S2

# Calculate Weight Vector
w = np.dot(np.linalg.inv(S), m1 - m2)

# Calculate Standard Value
b = (np.dot(w, m1) * len(omega1) + np.dot(w, m2) * len(omega2)) / (len(omega1) + len(omega2))

# Feature Vector
x = (9, 5, 4)

if np.dot(w, x) > b:
    print("omega 1.")
else:
    print("omega 2.")

实际上，判决用的判决边界值是该判别函数的标准截距。

支持向量机

支持向量

我们知道将训练样本分开的超平面可能有许多种，但是哪一个超平面是好的判决面呢？

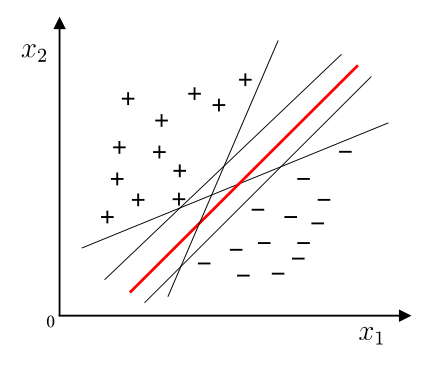
分类样本的多种超平面

很自然的我们会选择正中间的超平面，因为它的容忍性好，鲁棒性高，泛化能力最强。换句话说，它拥有的裕量大。

于是我们定义最优分类界面是给定线性可分样本集，能够将样本分开的最大间隔超平面。

其中，样本集与分类界面之间的距离 \(r\) 定义为样本与分类界面之间几何间隔的最小值。

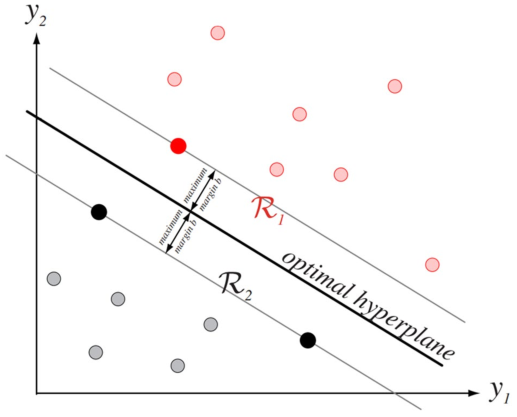
支撑向量示意图

我们把距离最优分类界面最近的这些训练样本称作支持向量，那么可以发现最优分类界面完全由支持矢量决定。

支持向量就像是维持超平面稳定的柱子。

然而支持向量的寻找比较困难。

我们将其转化，由判决函数 \[ g(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+b \] 知道解向量可以任意伸缩，同时保持超平面不变，即 \(g(\boldsymbol{x})=0\)。

现在缩放 \(\boldsymbol{w}\) 和 \(b\) 使得对 \(\omega_1\) 类的支持向量满足 \(g(\boldsymbol{x})=1\) 而对 \(\omega_2\) 类的支持向量满足 \(g(\boldsymbol{x})=-1\)。

那么可以用方程表示为 \[ \boldsymbol{w}^T\boldsymbol{x}_i+b\geq +1\\ \boldsymbol{w}^T\boldsymbol{x}_i+b\leq -1 \] 即 \[ z_kg(\boldsymbol{x}_k)\geq1 \] 模式属于 \(\omega_1\) 或是 \(\omega_2\) 我们分别令 \(z_k=\pm1\)。

由判决面性质可知，距离 \(r\) 满足 \[ r=\frac{g(\boldsymbol{x})}{\|\boldsymbol{w}\|} \] 定义间隔 \(\gamma=\frac{2}{\|\boldsymbol{w}\|}\)，其中可以知道支持向量上满足 \(r=\pm1\)。

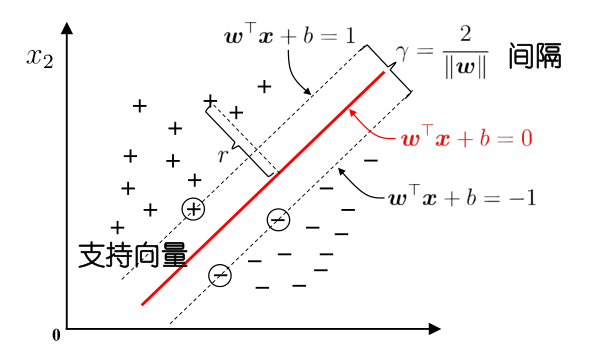
判决函数的支持向量性质

那么我们更进一步就是想使得间隔 \(\gamma\) 最大，不妨定义准则函数 \[ J(\boldsymbol{w})=\min_a\frac{1}{2}\|\boldsymbol{w}\|^2 \] 同时要满足 \[ z_kg(\boldsymbol{x})\geq 1 \] 但我们想要找到该准则函数的极小值，由于其带有约束条件，不能使用简单直接的梯度下降法。

不等式约束的极小值

朗格朗日定理

拉格朗日乘数法指出，要找到 \(z=f(x,y)\) 在约束条件 \(\varphi(x,y)=0\) 下的极值点，先构造拉格朗日函数 \[ L(x,y,\lambda)=f(x,y)+\lambda \varphi(x,y) \] 其中 \(\lambda\) 为某一常数。由 \[ \begin{cases} f_x(x,y)+\lambda\varphi_x(x,y)=0\\ f_y(x,y)+\lambda\varphi_y(x,y)=0\\ \varphi(x,y)=0 \end{cases} \] 解出 \(x,y,\lambda\)，其中 \(x,y\) 就是可能的极值点坐标。

将拉格朗日定理转化为与我们问题相关的形式，问题定义为 \[ \min f(\boldsymbol{x})\\ \text{s.t. }h_i(\boldsymbol{x})=0,i=1,2,\cdots,l \] 作出拉格朗日函数 \[ L(\boldsymbol{x},\boldsymbol{\lambda})=f(\boldsymbol{x})-\sum^{l}_{i=1}\lambda_ih_i(\boldsymbol{x}) \] 其中，\(\boldsymbol{\lambda}=(\lambda_1,\lambda_2,\cdots,\lambda_l)^T\) 称作乘子向量。

若 \(\boldsymbol{x}^*\) 是局部极小值，那么一定存在 \(\boldsymbol{\lambda}^*\) 满足 \[ \nabla_xL(\boldsymbol{x}^*,\boldsymbol{\lambda}^*)=0 \] 即 \[ \nabla_xf(\boldsymbol{x}^*)-\sum^{l}_{i=1}\lambda^*_i\nabla h_i(\boldsymbol{x}^*)=0 \]

KT 最优性条件

约束优化的一阶必要条件是由 Kuhn 和 Tuchker 于 1951 年提出，所以一阶必要条件又称为 KT 条件，满足 KT 条件的点又称作 KT 点。

KT 最优性条件是用于求解不等式约束的，问题定义如下 \[ \min f(\boldsymbol{x})\\ \text{s.t. }h_i(\boldsymbol{x})\geq0,i=1,2,\cdots,l \] 在拉格朗日定理的基础上，增加约束条件，即为 \[ \begin{cases} \nabla_xf(\boldsymbol{x}^*)-\sum^{l}_{i=1}\lambda^*_i\nabla h_i(\boldsymbol{x}^*)=0\\ h_i(\boldsymbol{x}^*)\geq0,\lambda_i^*\geq0,\lambda^*_ih_i(\boldsymbol{x}^*)=0,i=1,2,\cdots,l \end{cases} \] 这样就可以解决带不等式约束的极小值。

对偶问题

对偶问题是最优化问题的一个重要概念，它与原始问题相对应，通过对偶问题的解，可以推导出原始问题的解或相关信息。

对偶问题的主要思想是：将原问题中的部分约束条件转移到目标函数中，变为目标函数中的惩罚项。从而得到一个新的最优化问题，这就是对偶问题。

比如说一个原始问题是 \[ \min f(x)\\ \text{s.t. }c(x)=0,h(x)<=0 \] 其中 \(f(x)\) 是目标函数，\(c(x)=0\) 是等式约束，\(h(x)\leq 0\) 是不等式约束。

那么对应的对偶问题是 \[ \max g(u,v)=uc(x)+vh(x)\\ \text{s.t. }u\geq0,v\geq0 \]

支持向量机

依据上面的原理，我们可以得到支持向量机的模型可以转化为 \[ \begin{cases} \nabla\frac{1}{2}\|\boldsymbol{w}\|^2-\sum^{l}_{i=1}\lambda_i\nabla(z_kg(x_i)-1) =0\\ z_kg(x_i)-1\geq 0,\lambda_i\geq 0,\lambda_i g(x_i)=0 \end{cases} \] 一个两类分类问题有以下点 \[ \omega_1:(1,1),(1,-1)\\ \omega_2:(-1,1),(-1,-1) \] 通过以上知识，可以写出代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import sympy
import numpy as np

# Samples
omega1 = [(1, 1), (1, -1)]
omega2 = [(-1, 1), (-1, -1)]

samples = omega1 + omega2
sample_number = len(omega1) + len(omega2)
dimension = 2

# Initial
w0 = sympy.symbols('w0')
w = sympy.symbols(f'w1:{dimension+1}')
Lambda = sympy.symbols(f'\lambda_1:{sample_number+1}', nonnegative=True)
z = [1] * len(omega1) + [-1] * len(omega2)
L = np.dot(w, w) / 2
# Relaxtion Conditions
relaxtion_conditions = []
for i in range(sample_number):
    relaxtion_conditions.append(Lambda[i] * (z[i] * (np.dot(w, samples[i]) + w0) - 1))
    L -= relaxtion_conditions[-1]
# KT Conditions
KT_conditions = [sympy.diff(L, w0)]
for wi in w:
    KT_conditions.append(sympy.diff(L, wi))
# w0 Conditions
basis_conditions = [w0]
# Total Conditions
conditions = KT_conditions + relaxtion_conditions + basis_conditions

# Solve
result = sympy.solve(conditions)

# Find all solutions besides 0 solution
w_sets = set()
for i in result:
    w_set = [i[wi] for wi in w]
    # Besides 0 solution
    if w_set.count(0) == len(w_set):
        continue
    w_sets.add(tuple(w_set))
print(w_sets)
"""
{(1, 0)}
"""
支持向量机的解

以下是等价问题的转换。

由基本的支持向量机公式，我们有拉格朗日函数 \[ L(\boldsymbol{w},\lambda_i)=\frac{1}{2}\|\boldsymbol{w}\|^2-\sum^{l}_{i=1}\lambda_i\nabla(z_kg(\boldsymbol{x}_i)-1) \] 令拉格朗日函数偏导为零，代入公式可得 \[ \max_\boldsymbol{\lambda} L(\boldsymbol{\lambda})=\sum_{i=1}^l\lambda_i-\frac{1}{2}\sum^l_{k,j=1}\lambda_k\lambda_jz_kz_j\boldsymbol{x}_k^T\boldsymbol{x}_j\\ \text{s.t. }\sum_{i=1}^l\lambda_iz_i=0,\lambda_i\geq 0 \] 即等价于二次规划问题。

比如说我们有二分类问题，样本为 \[ \omega_1:\boldsymbol{x}_1=(3,3),\boldsymbol{x}_2=(4,3)\\ \omega_2:\boldsymbol{x}_3=(1,1) \] 解 \[ \min_\boldsymbol{\lambda}\frac{1}{2}\sum^l_{k,j=1}\lambda_k\lambda_jz_kz_j\boldsymbol{x}_k^T\boldsymbol{x}_j-\sum_{i=1}^l\lambda_i\\ =\frac{1}{2}(18\lambda_1^2+25\lambda_2^2+2\lambda_3^2+42\lambda_1\lambda_2-12\lambda_1\lambda_3-14\lambda_2\lambda_3)-\lambda_1-\lambda_2-\lambda_3\\ \text{s.t. }\lambda_1+\lambda_2-\lambda_3=0,\lambda_i\geq0,i=1,2,3 \] 将约束条件 \(\lambda_3=\lambda_1+\lambda_2\) 带回目标函数得到 \[ s(\lambda_1,\lambda_2)=4\lambda_1^2+\frac{13}{2}\lambda_2^2+10\lambda_1\lambda_2-2\lambda_1-2\lambda_2 \] 求 \(\nabla s=0\)，得到 \(s(\lambda_1,\lambda_2)\) 在 \((\frac{3}{2},-1)\) 上取极值，但不满足 \(\lambda_i\geq 0\) 的约束条件，故在边界上找最小值。

当 \(\lambda_1=0\) 时，最小值 \(s(0,\frac{2}{13})=-\frac{2}{13}\)；

当 \(\lambda_2=0\) 时，最小值 \(s(\frac{1}{4},0)=-\frac{1}{4}\)。

故取最小值 \(\lambda_1=\frac{1}{4},\lambda_2=0,\lambda_3=\frac{1}{4}\)，这样，\(\boldsymbol{x}_1,\boldsymbol{x}_3\) 为支持向量。

利用 KT 条件反求得到 \(w_1=w_2=\frac{1}{2},b=-2\)，故分离超平面为 \[ \frac{1}{2}x_1+\frac{1}{2}x_2-2=0 \]

核函数

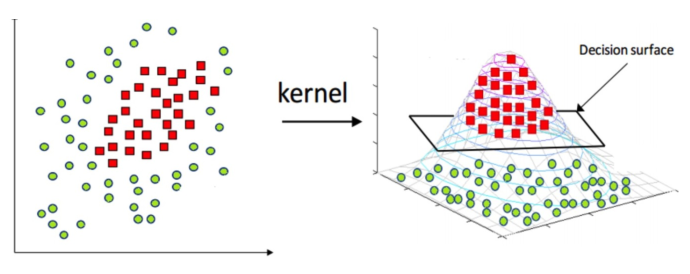
对于线性不可分问题，我们需要将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分，而映射的特征是基于原本特征的数学意义上的拓展特征。

那么我们就可以将原本的特征向量作映射，将支持向量机的模型拓展为 \[ \max_\boldsymbol{\lambda} L(\boldsymbol{\lambda})=\sum_{i=1}^l\lambda_i-\frac{1}{2}\sum^l_{k,j=1}\lambda_k\lambda_jz_kz_j\phi(\boldsymbol{x}_k)^T\phi(\boldsymbol{x}_j)\\ \text{s.t. }\sum_{i=1}^l\lambda_iz_i=0,\lambda_i\geq 0 \] 其中，\(\phi(\boldsymbol{x})\) 是映射函数，也称核映射，即将 \(l\) 维的特征空间映射到更高维的特征空间。

那么分离超平面则为 \[ f(\boldsymbol{x})=\boldsymbol{w}\phi(\boldsymbol{x})+b \] 核映射的一个示意图

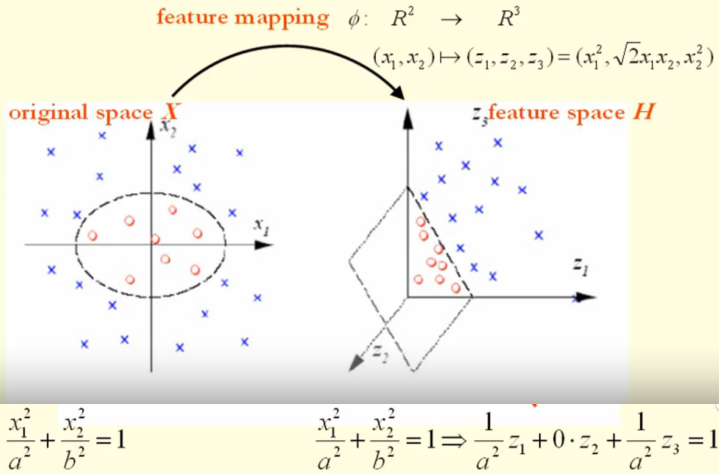
比如说一个可能的核映射函数是从 \(R^2\to R^3\)，即 \[ (x_1,x_2)\to(z_1,z_2,z_3)=(x_1^2,\sqrt{2}x_1x_2,x_2^2) \] 一个二维到三维的核映射

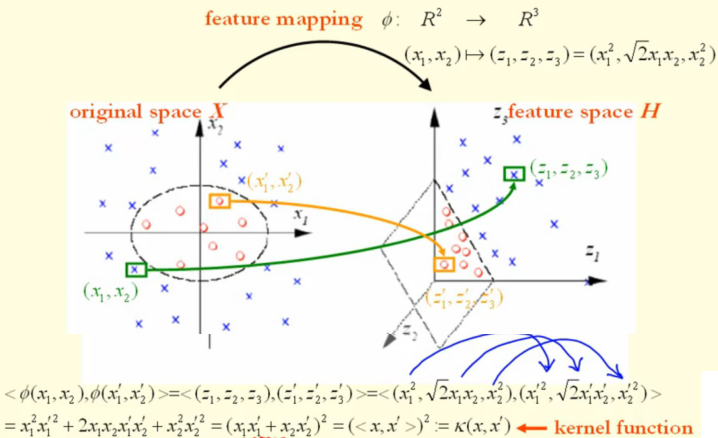
但我们知道，如果计算核映射，且计算高纬度的核映射，我们不仅需要设计一个好的核映射，还必须快速的去计算它，这是复杂的。

那么，我们可以发现，在约束中实际上核映射后的结果仅以内积的形式呈现，不妨我们设计一个核函数 \[ k(\boldsymbol{x}_i,\boldsymbol{x}_j)=\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x}_j) \] 这样我们就可以不显式地设计核映射，而是设计核函数。（基本想法）

比如对于上面例子中的核映射，我们可以计算得到其核函数为 \[ k(\boldsymbol{x}_i,\boldsymbol{x}_j)=(\boldsymbol{x}_i^2+\boldsymbol{x}_j^2)^2 \] 核函数的一个设计实例

常用核函数

核支持向量机

基于核函数的思想，我们可以得到一个新的支持向量机模型，即核支持向量机模型 \[ \max_\boldsymbol{\lambda} L(\boldsymbol{\lambda})=\sum_{i=1}^l\lambda_i-\frac{1}{2}\sum^l_{k,j=1}\lambda_k\lambda_jz_kz_jk(\boldsymbol{x}_k,\boldsymbol{x}_j)\\ \text{s.t. }\sum_{i=1}^l\lambda_iz_i=0,\lambda_i\geq 0 \] 例如对于在二位特征平面上线性不可分问题 XOR 问题，我们可以设计一个核函数为 \[ k(\boldsymbol{x}_i,\boldsymbol{x}_j)=[1+\boldsymbol{x}_i^T\boldsymbol{x}_j]^2 \] 使其在该空间上是线性可分的，一个可以构成这个核函数的核映射为 \[ \phi(\boldsymbol{x})=(1,\sqrt{2}x_1,\sqrt{2}x_2,\sqrt{2}x_1x_2,x_1^2,x_2^2) \] XOR 问题中， \[ \omega_1:\boldsymbol{x}_1=(1,1),\boldsymbol{x}_3=(-1,-1)\\ \omega_2:\boldsymbol{x}_2=(1,-1),\boldsymbol{x}_4=(-1,1) \] 计算过程忽略，我们可以得到 \[ L(\boldsymbol{\lambda})=\lambda_1+\lambda_2+\lambda_3+\lambda_4\\-\frac{1}{2}(9\lambda_1^2-2\lambda_1\lambda_2-2\lambda_1\lambda_3+2\lambda_1\lambda_4\\+9\lambda_2^2+2\lambda_2\lambda_3-2\lambda_2\lambda_4\\+9\lambda_3^2-2\lambda_3\lambda_4\\+9\lambda_4^2) \] 最终得到 \(\lambda_1=\lambda_2=\lambda_3=\lambda_4=\frac{1}{8}\)，四个样本均为支持向量。

最终解得最优分离超平面为 \[ f(\boldsymbol{x})=-x_1x_2=0 \]