传感器与检测技术笔记
传感器与检测技术
绪论
为什么需要
一个典型的反馈控制系统框图如下
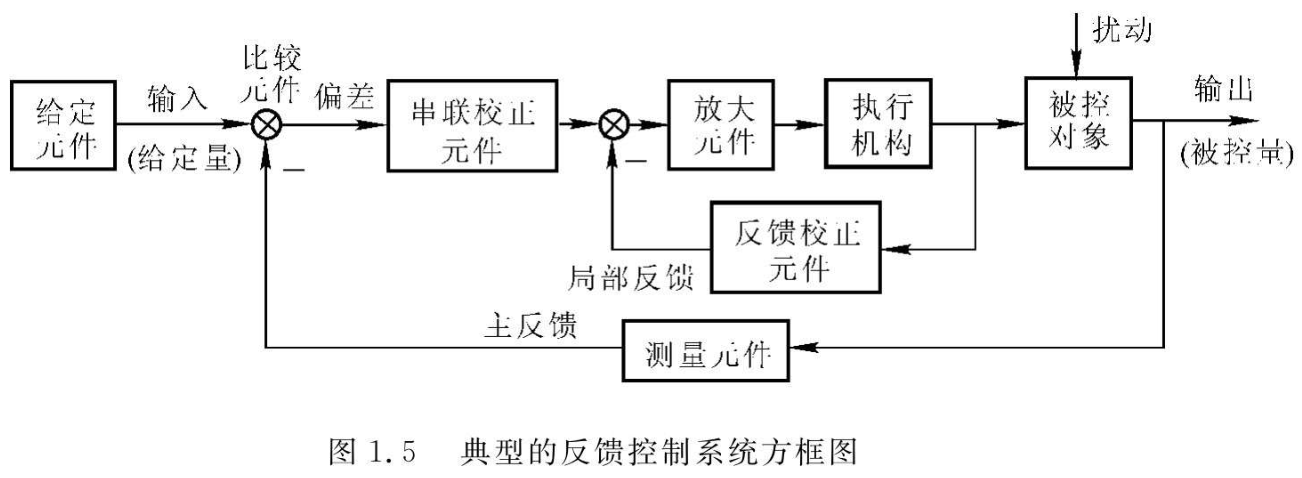
从系统框图中不难看出,一个反馈控制系统中最关键的是反馈部分,没有反馈就无法利用控制算法进行控制,反馈在先而控制在后。
而反馈部分中最关键的就在于我们要怎么让机器理解被控量大了还是小了,多了还是少了,而解决这个问题的就是传感器与测量技术。
什么是传感器
传感器的英文是 sensor,其词根是 sense —— 感觉。
很显然,对于人来说,眼睛就是传感器,而视觉就是一种感觉,将感觉转换成了生物电信号使得大脑可以处理。
而对于机器而言也是这样,传感器将感觉转换成电信号(也可以是光信号)使得控制系统可以处理。
总结成定义就是:传感器是一种把特定的被测信息量按照一定规律转换成为可用信号输出的器件或装置,即将非电信号转换成特定形式的电信号。
特定的被测信息量可以是物理量、化学量或者生物量等。
可用信号是便于处理和传输的非噪声信号,如电信号和光信号。
一定规律是确定性的,可重复的(线性、非线性、周期)
例如说初中学过的压电陶瓷,它将力在一定范围内按照线性规律转换成为电压信号,其中
- 特定的被测信息量:力
- 可用信号:电压信号
- 一定规律:压电陶瓷在一定范围内力所造成的形变与所产生的电压满足线性规律
或者说热敏电阻,其将温度变化转换为电阻变化。
但以上材料仅是传感器的一部分,它们的输出是不稳定的,真正的传感器由三部分组成:
- 敏感元件:它直接感受被测量,并输出与被测量成确定关系的某一物理量的元件,例如上面提到的压电陶瓷和热敏电阻
- 转换元件:敏感元件的输出是它的输入,它将输入转换成电路参数,例如运算放大器,用于放大热敏电阻很小的电阻变化产生的电压信号
- 转换电路:将转换元件的输出作为输入,转换为计算机可理解的电压信号,例如模数转换,将模拟量转换为数字电路可以理解的数字量
转换元件也有可能是机械的,比如说弹簧作为敏感元件产生的输出是力信号而不是电信号,此时需要应变片将力信号再转换为电信号。
什么是检测技术
检测技术是指用于检测、测量和识别的技术和方法。这些技术和方法用于将传感器提供的信号进行处理、分析和解释,以得到准确的测量结果和信息。
例如说现实中测量得到的信号可能会夹杂一定的白噪声,我们希望得到尽量没有白噪声的理论数据。
- 检:力图发现对象中的某些待测量并以信号的形式表现出来
- 测:量化待测量的信号
什么是检测系统
一个检测系统由多个传感器串联或并联形成,单输出或多输出。
检测技术基本理论
国际单位制
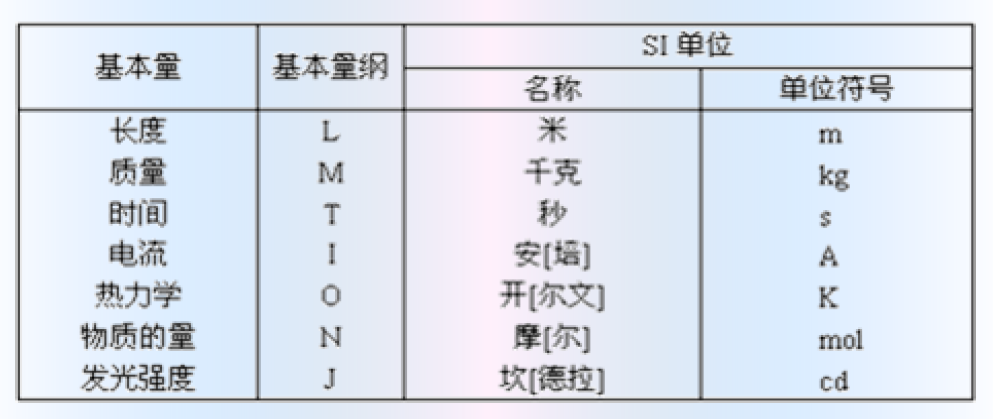
传感器的基本特性
一个单输入单输出的系统框图如下
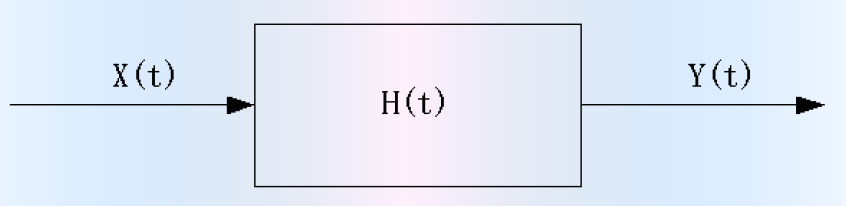
一般的工程测试问题总是处理输入量 \(x(t)\),系统的传输转换特性 \(h(t)\) 和输出量 \(y(t)\) 的关系:
- 系统辨识:当输入、输出是可测量的(已知的),可以通过它们推断系统的传输特性。
- 反求:当系统特性已知,输出是可测量的,可以通过它们推断系统的输入量。
- 预测:当系统特性已知,输入是可测量的,可以通过它们推断系统的输出量。
在一个测量系统中,最重要的是要搞清楚谁是输入,谁是输出。
所以一个传感器的基本特性是输出与输入之间的关系,细分为:
- 传感器的静态特性:输入量为常量或随时间变化极慢
- 传感器的动态特性:输入量随时间变化较快
静态特性
当输入量为常量或随时间变化极慢时,不考虑传感器的迟滞和蠕变因素,可以用数学公式表示为 \[ y=a_0+a_1x+a_2x^2+\cdots+a_nx^n \] 其中 \(x\) 为输入量;\(y\) 为输出量;\(a_0\) 为零位输出;\(a_1\) 为传感器的灵敏度;\(a_2,\cdots,a_n\) 为非线性项的待定系数。
线性度
传感器的线性度(又称非线性误差)是指传感器的输出与输入之间的线性程度。
通常为了方便标定和数据处理,理想的输出输入关系应该是线性的,但实际遇到的传感器的特性大多是非线性的。
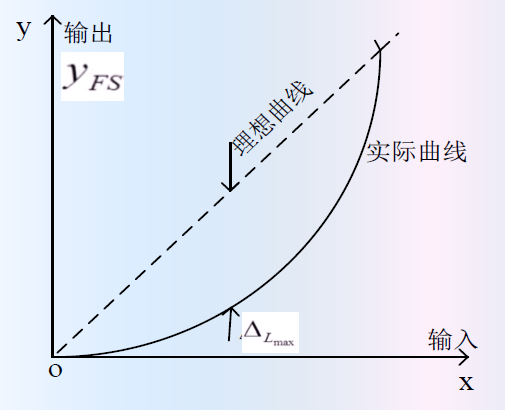
其中,\(y_{FS}\) 是满量程输出,是传感器测量范围的上下限输出值的差值,也称输出满度值。
而 \(\Delta L_{max}\) 是最大非线性绝对误差,是实际特性曲线和拟合直线之间的最大误差。
而线性度就是最大非线性绝对误差比上满量程输出的比值,用于度量理想关系与实际关系的差别,即 \[ \gamma_L=\pm\frac{\Delta L_{max}}{y_{FS}}\times 100\% \]
需要注意,一定是先有理想线性关系(理想直线、近似直线)才能计算线性度。
为了提高线性度,使得传感器特性接近于理想线性关系,通常会采用以下几种方式进行直线拟合:
- 理论拟合:拟合直线取理想线性关系(理想直线、近似直线)
- 过零旋转拟合:使得 \(|\Delta L_1|=|\Delta L_2|=|\Delta L_{max}|\)
- 端点连线拟合:拟合直线取曲线两端点的连线(拉格朗日)
- 端点连线平移拟合:端点连线后使得 \(|\Delta L_1|=|\Delta L_2|=|\Delta L_3|=|\Delta L_{max}|\)
- 最小二乘法拟合
- 差动法
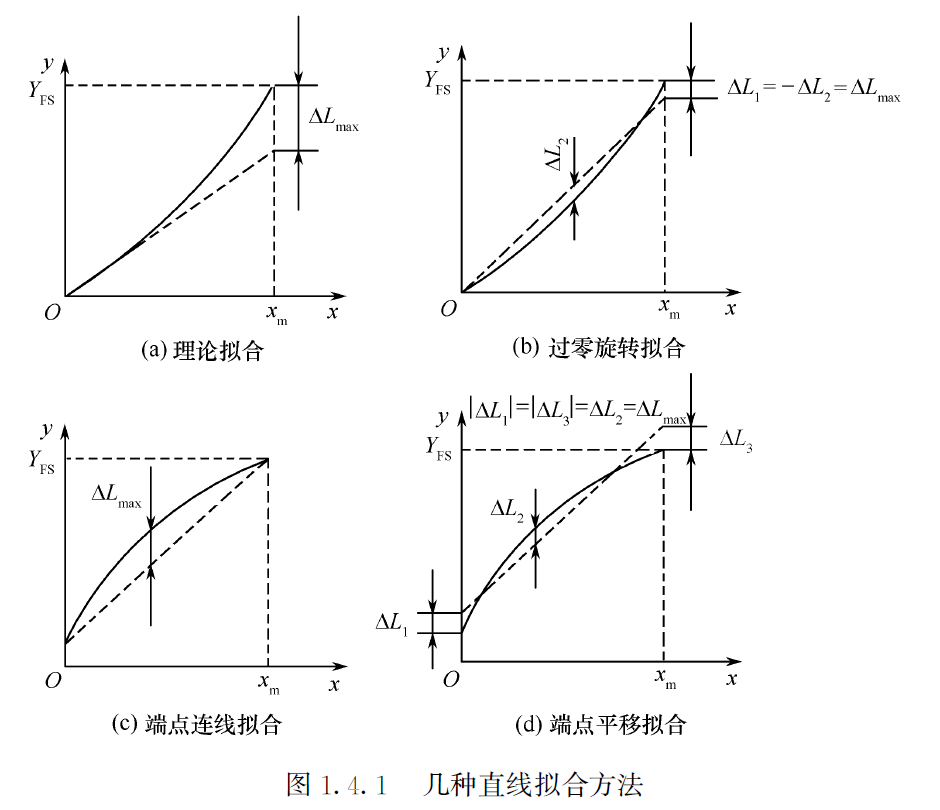
其中,最小二乘法是最好的直线拟合方法,其可以使得非线性误差最小,但需要进行程序计算,拟合直线为 \[ y=kx+b \] 其中斜率 \[ k=\frac{\sum^n_{i=1}(x_i-\bar{x})(y_i-\bar{y})}{\sum^n_{i=1}(x_i-\bar{x})^2} \] 截距 \[ b=\bar{y}-k\bar{x} \] 特点是拟合直线一定过数据均值点。
不过方差过大(非线性很强)的数据仅使用最小二乘法也是无意义的,所以一般还会配合差动法补偿曲线的非线性。
考虑两个关系式 \[ y=a_1x+a_3x^3+\cdots\\ y=a_2x^2+a_4x^4+\cdots\\ \] 很显然,偶次项中非线性系数更多,所以我们可以尝试找到两个输入(可能是堆成的 \(\pm x\))使得 \[ y_1=a_0+a_1x+\cdots+a_nx^n\\ y_2=a_0+a_1(-x)+\cdots+a_n(-x)^n\\ \] 那么我们将两式相减,就得到 \[ \Delta y=y_1-y_2=2(a_1x+a_3x^3+\cdots) \] 这样可以显著改善线性范围,使得灵敏度提高一倍。
灵敏度
定义:单位输入变化量引起的输出变化量的比值
意义:表征传感器对输入量变化的反应能力
公式: \[ S=\frac{\Delta y}{\Delta x} \] 传感器输出曲线的斜率就是其灵敏度,对于线性特性的传感器灵敏度与输入量大小无关。
输出特性为曲线那么需要求拟合直线的斜率即可。
一般来说希望传感器灵敏度高(高精度),在满量程范围内恒定(线性特性)。
对于线性检测系统来说,串联的各环节灵敏度相乘得到总灵敏度。
迟滞
迟滞也称滞后度、回程误差、变差。
指的是传感器在正(输入量增大)反(输入量减小)行程期间,特性曲线不重合的现象。
常因有弹性敏感元件的弹性滞后,磁性敏感元件的磁滞现象等。
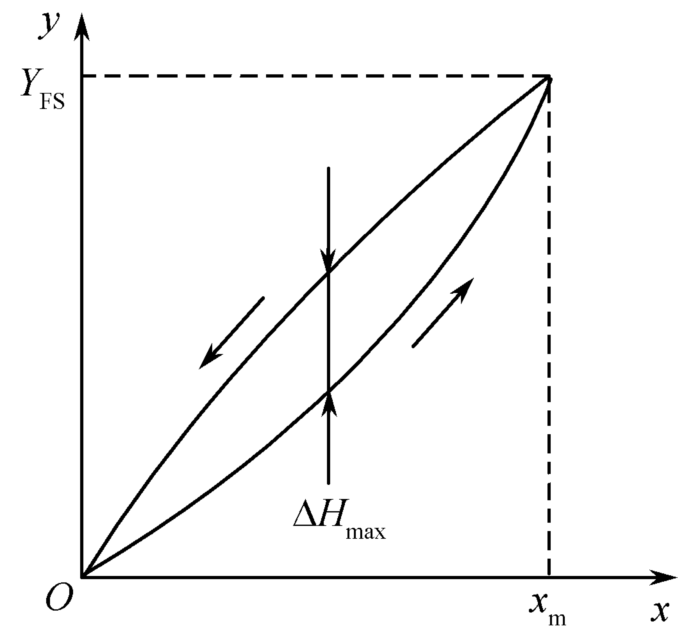
计算公式为 \[ \gamma_H=\frac{|\Delta H_{max}|}{Y_{FS}}\times 100\% \] 其中 \(\Delta H_{max}\) 是最大迟滞差。
重复性
重复性是检测系统最基本的技术指标,是其他各项指标的前提和保证,尤其对于高精度测量任务。
我们希望在有限次测量中,测量结果一致。
同一条件下,同一被测量,同一方向,多次重复测量的差异程度。
一般取三次测量,故也简称三同三次。
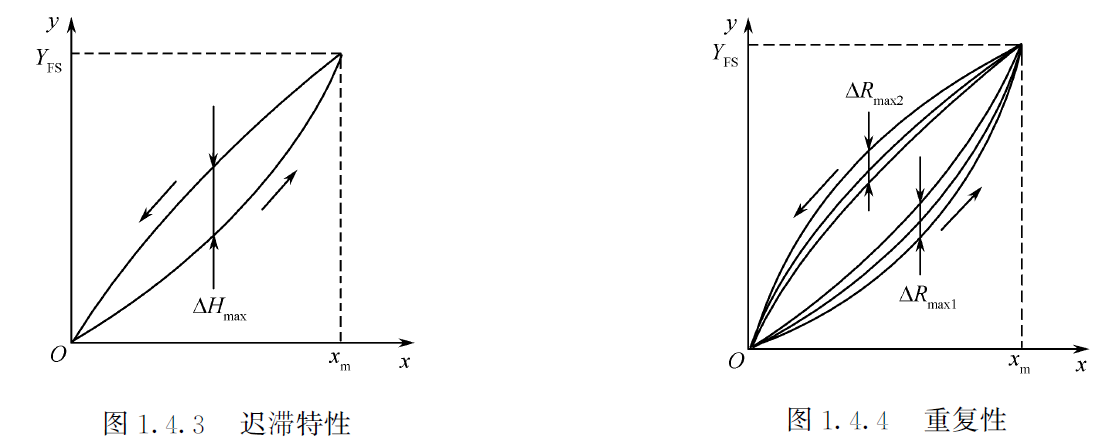
重复性跟迟滞是存在一定关系的,公式为 \[ \eta =\frac{|\Delta R_{max}|}{Y_{FS}}\times 100\% \] 其中,\(\Delta R_{max}\) 是正行程的最大重复性偏差或反行程的最大重复性偏差(取更大值)。
不同书上有不同定义。
分辨力
分辨力指的是当改变输入时,导致输出能够发生变化的最小临界值,是传感器显示装置的判别特性。
分辨力有效的辨别紧密相邻量值的能力,跟灵敏度有一定联系,用绝对值表示。
分辨力与满量程的百分比称为分辨率。
在传感器输入零点附近的分辨力称为阈值,即是使得传感器有输出的值。
对于不同的仪表其分辨力的标准是不同的。
- 模拟表:取最小刻度的一半,例如直尺的最小刻度是 1mm,那么其分辨力是 0.5 mm = 0.0005 m
- 数字表:取最后一位数字,例如数字仪表显示 4.5 度,那么分辨力为 0.1 度。
分辨力只与显示有关,与传感器精度无关,例如分辨力为 0.01 度的电子温度计,实际温度 60.00 度,测量温度是 51.09 度,可以说其分辨力高,但是其精度是低的。
分辨力我愿称为显示精度。
一般取分辨率为测量精度的 \(1/3\sim 1/5\),分辨率过低不能够保证精度要求;而过高则是浪费。
灵敏度与测量范围
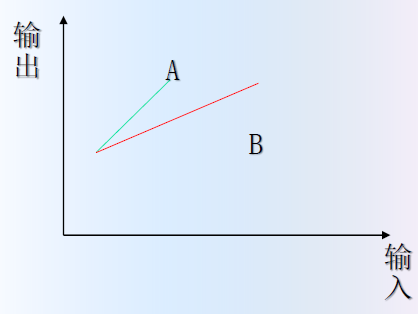
参考上图,我们不难知道传感器 A 比传感器 B 的灵敏度更高,从测量尺度的角度来说测量精度也更高。
所以,灵敏度往往是优化传感器性能的一个重要指标。
但是光有精度是不够的,我们还要考虑测量范围的大小,显然传感器 B 的测量范围要比传感器 A 更大。
所以,实际设计传感器时,往往需要考虑平衡测量范围和灵敏度。
精确度
精确度可分为
- 精密度:数据分散程度
- 准确度:与真值偏离程度
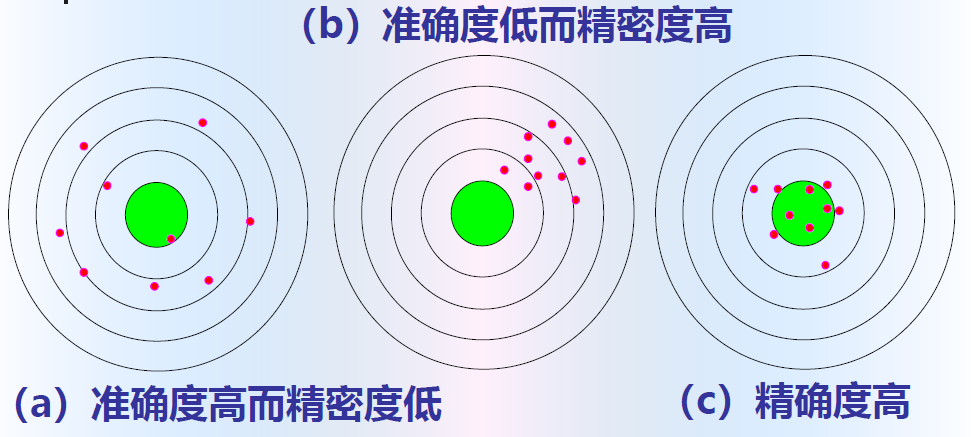
精确度是两者的综合。
温漂
温漂表示温度变化时传感器输出值的偏离程度。 \[ \frac{\Delta max}{Y_{FS}\Delta T}\times 100\% \] 其中,\(\Delta max\) 是输出最大偏差,\(\Delta T\) 是温度变化范围,\(Y_{FS}\) 是满量程输出(只看最大值)。
信噪比
用功率表示为 \[ \mathrm{SNR}=10\lg\frac{P_s}{P_n} \] 用信号幅值表示为 \[ \mathrm{SNR}=20\lg\frac{V_s}{V_n} \]