Pollard's rho method笔记

发表于 更新于 本文字数： 1.9k 阅读时长 ≈ 2 分钟
有关Pollard's rho method分解算法的简要笔记

Pollard's rho method

原理

生日悖论

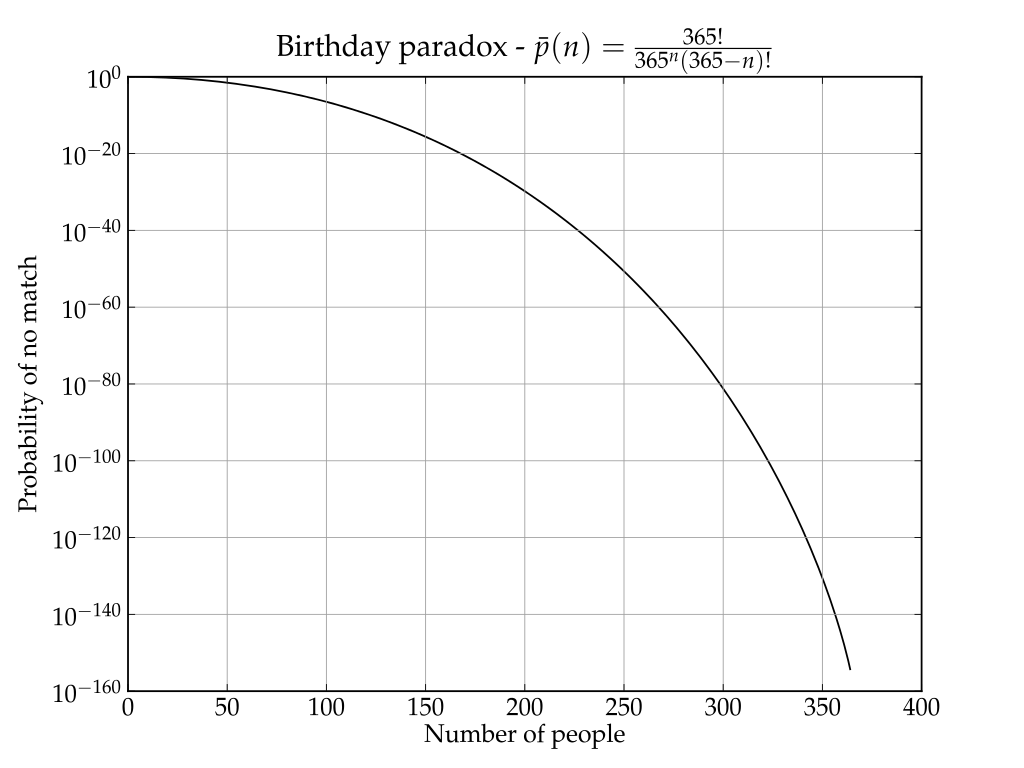
在概率论中，生日问题要求在一组随机选择的 \(n\) 个人中，至少有两人生日相同的概率。生日悖论指的是违反直觉的事实，即该概率超过 50% 只需要 23 个人 。

从条件概率原理的角度来看，可以知道 \[ \begin{align} \bar{p}(n)&=1\times\left(1-\frac{1}{365}\right)\times\left(1-\frac{2}{365}\right)\times\cdots\times\left(1-\frac{n-1}{365}\right)\\ &=\frac{365\times364\times\cdots\times(365-n+1)}{365^n}\\ &=\frac{_{365}P_n}{365^n} \end{align} \] 其中 \(_kP_n\) 表示排列。

img

rho method

假设 \(N=pq\)，其中 \(p\) 为 \(N\) 的一个非平凡因子，使用一个模 \(N\) 多项式 \(g(x)\) 生成随机序列 \(\{x_i\mod{N}\}\)。

选择一个初始值 \(x=2\)，计算 \(x_1=g(2),x_2=g(g(2)),\cdots\)。

由于其为模 \(N\) 多项式生成的序列值，故序列值必会重复。

而由生日悖论的原理可以知道，\(x_i\) 重复出现的概率为 \(O(\sqrt{N})\)。所以对于序列 \(\{x_i\mod{p}\}\) 会更早地出现重复值。

当找到 \(x_{i1}\neq x_{i_2}\) 但 \(x_{i1}= x_{i_2}\pmod{p}\) 时，\(|x_{i1}-x_{i_2}|\) 即为 \(p\) 的倍数。

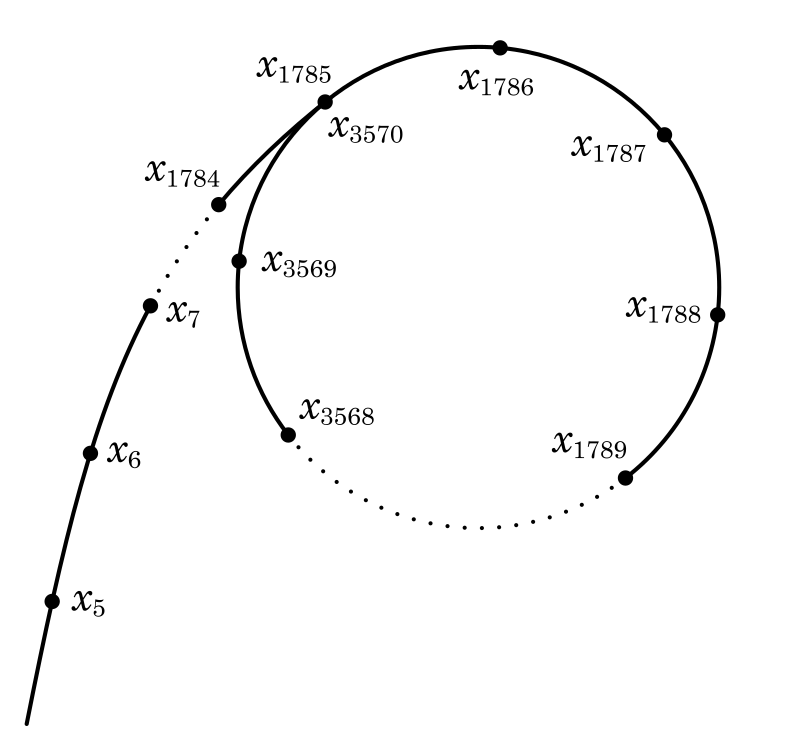
由于序列中的每个值只依赖于它之前的值，且构成的循环画在图上就像是希腊字母 \(\rho\) 一样，故称为 rho method。

img

该算法的时间复杂度为 \(\displaystyle{O(N^{\frac{1}{4}}+\frac{N^{\frac{1}{4}}\alpha(N)}{\beta}+\beta\alpha(N))}\)。

Floyd 判环法

Floyd 判环法又称龟兔赛跑法。

我们让 \(t,h\) 指向起始序列值（一般选取 2），让 \(t\) 和 \(h\) 的移动速度不同，即每次 \(t=g(t)\)，\(h=g(g(h))\)，只要二者可以前进且没有相遇，就前进下去。

当 \(t=h\) 时，可以确定已经进入到了环中。

在 rho method 中即 \(|t-h|\) 为 \(p\) 的倍数。

Brent 判环法

Brent 判环法又称传送乌龟法。

我们让 \(t,h\) 指向起始序列值，但 \(t\) 先不动，\(h\) 每次只走一步，即 \(h=g(h)\)，在第 \(i\) 次中最多走 \(2^i\) 步，在二者没有相遇时就前进下去。当 \(h\) 在本次移动完毕后，将 \(t\) 移动到 \(h\) 处，即 \(t=h\)。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import random
try:
    gcd
except NameError:
    from math import gcd

def rho(N):
    f = lambda x: (x ** 2 + 1) % N
    while True:
        # 加快入环速度
        t = random.randint(2, N)
        h = f(t)
        while True:
            p = gcd(abs(int(t) - int(h)), N)
            if p == N:
                break
            elif p > 1:
                return (p, N // p)
            else:
                t = f(t)
                h = f(f(h))

print(rho(15405314906656169587))

另一种判环法，效率相对高一些

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import itertools
import random
try:
    gcd
except NameError:
    from math import gcd

def rho(N):
    f = lambda x: (x ** 2 + 1) % N
    while True:
        # 加快入环速度
        t = random.randint(2, N)
        h = f(t)
        step_times = 0
        step_limit = 2
        while True:
            if not step_times < step_limit:
                step_times = 0
                step_limit *= 2
                t = h
                h = f(h)
            p = gcd(abs(int(t) - int(h)), N)
            if p == N:
                break
            elif p > 1:
                return (p, N // p)
            else:
                h = f(h)
                step_times += 1

print(rho(14354303587370996407))