最优化方法——最优性条件
最优化方法
最优性条件
所谓最优性条件,是指最优化问题的最优解所要满足的必要条件或充分条件,这些条对于最优化算法的建立和最优化理论的推导都是至关重要的,有的算法甚至可以直接用来求解问题。
无约束问题
对于无约束问题,函数 \(f(x)\) 的最优性条件是
一阶必要条件 \[ \nabla f(x^*)=0 \]
二阶必要条件 \[ \begin{cases} \nabla f(x^*)=0\\ \nabla^2 f(x^*)\text{半正定} \end{cases} \]
二阶充分条件 \[ \begin{cases} \nabla f(x^*)=0\\ \nabla^2 f(x^*)\text{正定} \end{cases} \]
有约束极值问题
有约束的极值问题一般表示为 \[ \begin{align} \min &f(x),x\in R^n\\ \text{s.t. }g_i(x)&\geq 0,i=1,\cdots,m\\ h_j(x)&= 0,j=1,\cdots,l \end{align} \] 其中 \(g_i(x)\geq0\) 称为不等式约束,\(h_j(x)=0\) 称为等式约束。
对于集合 \[ S=\left\{x\middle|\begin{align} g_i(x)&\geq 0,i=1,\cdots,m\\ h_j(x)&= 0,j=1,\cdots,l \end{align}\right\} \] 称为可行集合或可行域。
基于以上概念,我们可以将有约束的极值问题分解为等式约束和不等式约束。
拉格朗日乘数法
等式约束最优化问题如下所示 \[ \begin{align} \min &f(x),x\in R^n\\ \text{s.t. }c_j(x)&= 0,j=1,\cdots,l \end{align} \] 对于该问题一般采用拉格朗日乘数法解决。
构造拉格朗日函数 \[ L(x,\mathbf {\lambda})=f(x)-\lambda^Tc(x) \] 其中,\(\lambda=(\lambda_1,\lambda_2,\cdots,\lambda_l)^T\) 称作拉格朗日乘子向量,
\(c(x)=(c_1(x),c_2(x),\cdots,c_l(x))^T\) 是约束函数向量。
那么求拉格朗日函数的梯度 \[ \nabla L(x,\lambda)=\begin{bmatrix} \nabla_x L(x,\lambda)\\ \nabla_\lambda L(x,\lambda) \end{bmatrix} \] 其中,\(\nabla_x L(x,\lambda)=\nabla f(x)-\sum \lambda_j\nabla c_j(x)\),\(\nabla_\lambda L(x,\lambda)=-c(x)\)。
最优性条件(一阶必要条件)如下:
- \(f(x)\) 与 \(c_j(x)\) 在 \(x^*\) 邻域内一阶连续可微
- \(\nabla c_j(x)\) 线性无关(否则不可逆)
- 那么存在一组不全为 0 的乘子向量 \(\lambda^*\) 使得 \(\nabla L(x^*,\lambda^*)=0\)
几何意义:目标函数在极值点处的梯度可表示为关于约束函数在该点处梯度的线性组合。
约束只有一个时,共线(平行)。
这样,我们就将等式约束最优化问题转化为无约束最优化问题求解。
但这样只能求解出稳定点(极小点或鞍点),如果需要验证是否为严格局部极小点,仍需二阶充分条件:
- \(f(x)\) 与 \(c_j(x)\) 在 \(x^*\) 邻域内二阶连续可微
- 存在一组不全为 0 的乘子向量 \(\lambda^*\) 使得 \(\nabla L(x^*,\lambda^*)=0\)
- 对于约束集 \(S=\{s\in R^n|s\neq 0,s^T\nabla c_j(x^*)=0,j=1,\cdots,l\}\),均满足 \(s^T\nabla^2_{xx} L(x^*,\lambda^*)>0\)
例如等式最优化问题 \[ \begin{align} \min f(x)&=x_1^2+x_2^2\\ \text{s.t. }h(x)&=x_1x_2-8=0 \end{align} \] 构建拉格朗日函数 \[ L(x,\lambda)=x_1^2+x_2^2-\lambda(x_1x_2-8) \] 求梯度,有 \[ \nabla L(x,\lambda)=\begin{bmatrix} 2x_1-\lambda x_2\\ 2x_2-\lambda x_1\\ -(x_1x_2-8) \end{bmatrix} \] 由梯度为 0 解得平稳点 \[ \begin{bmatrix} \sqrt{8}\\ \sqrt{8}\\ 2 \end{bmatrix}, \begin{bmatrix} -\sqrt{8}\\ -\sqrt{8}\\ 2 \end{bmatrix} \] 求二阶导 \[ \nabla^2_{xx}L(x,\lambda)=\begin{bmatrix} 2&-\lambda\\ -\lambda&2 \end{bmatrix} \] 求约束函数的梯度 \[ \nabla h(x)=\begin{bmatrix} x_1\\ x_2 \end{bmatrix} \] 那么对于平稳点 \([\sqrt{8},\sqrt{8},2]^T\),有 \(x^*=[\sqrt{8},\sqrt{8}]^T,\lambda^*=2\),求解约束集 \[ \begin{align} s&=(s_1,s_2)^T\\ s^T\nabla h(x^*) =0&\to S=\{s|s_1+s_2=0\} \end{align} \] 对于约束集的任意元素,有 \[ s^T\nabla^2_{xx}L(x^*,\lambda^*)s=2s_1^2-4s_1s_2+2s_2^2=8s_1^2>0 \] 故该点为严格局部极小点。
同理,平稳点 \([-\sqrt{8},-\sqrt{8},2]^T\) 也为严格局部极小点。
对偶问题
对偶问题(Dual Problem)是用于求解原问题(Primal Problem)的巧妙思路,有的时候对偶问题的求解可能要比原问题简单(蕴含反证法的本质思想)。
例如说我们有原优化问题 \[ \begin{align} \max z&=cx\\ \text{s.t. }Ax&\leq b\\ x&>0 \end{align} \] 其中 \(c_{1\times n},A_{m\times n},x_{n\times 1},b_{m\times 1}\)。
我们作以下变换,对不等式约束两边相乘以一个非负向量 \(y_{m\times 1}\geq 0\),变形为 \[ y^TAx\leq y^Tb \] 对于任意一个 \(y^*\) 都会有 \[ cx\leq (y^*)^TAx\leq (y^*)^Tb \] 即 \((y^*)^Tb\) 成为了原问题的一个上界,那么此时我们在上界范围中寻找最小的上界,显然其就是原问题目标函数的最优值。
即将问题转化为 \[ \begin{align} \min w&=b^Ty\\ \text{s.t. }A^Ty&\geq c^T\\ y&\geq0 \end{align} \] 这就是原问题的对偶问题。
多说无益,细细品味上面的逻辑关系。
在这里也给出一个通俗易懂的理解:将问题从瘦子堆中挑选最胖的胖子(从下界中寻找最大的下界)转化为从胖子堆中挑选最瘦的瘦子(从上界中寻找最小的上界)。
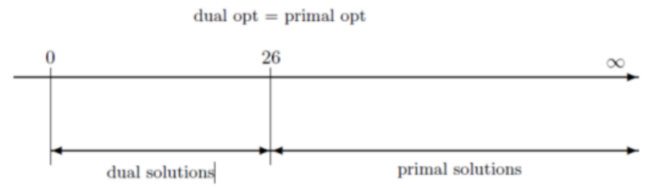
可以从上图中体会对偶问题的解和原问题的解的关系,其中 26 是目标函数最优值,两个问题分别从左右两侧逼近最优值。
但是对偶问题有时不一定比原问题简单计算,在最优化问题中通常在以下情境下利用对偶问题求解最优化问题:
- 对偶问题总是凸优化问题
- 原问题约束少、变量多时,求解对偶问题能够降低计算时间,如果原问题约束少变量多,转换成对偶问题,就是约束多变量少。变量的减少能够有效降低计算时间。有些情况下,反之亦然
- 灵敏度问题
- 更容易求解,如结构更好
但很明显可以察觉到,不是所有的对偶问题的上界的最小值恰好是原问题下界的最大值(反之亦然),为了区分这一情况,我们将对偶关系分为弱对偶(weak duality)和强对偶(strong duality)。
我们假设 \(d^*\) 是对偶问题的最优解,而 \(p^*\) 是原问题的最优解,很显然强对偶关系就是上面所描述的恰好 \(d^*=p^*\) 的情况。
而弱对偶关系描述的正是对偶问题的上界的最小值不恰好是原问题下界的最大值(反之亦然),即 \(d^*\geq p^*\),而同时 \(d^*-p^*\) 称为对偶间隙(duality gap)。
Slater 条件
定义1:对于一个凸问题,若存在 \(x\in D\),其中 \(D\) 为凸集,使得 \(f_i(x)<0,i=1,\cdots,m\) 且 \(Ax=b\),那么该凸问题和它的对偶问题一定是强对偶。
定义2:对于一个凸问题,若不等式约束为仿射约束,只要可行域非空,那么该凸问题和它的对偶问题一定是强对偶。
一般的凸问题都满足 Slater 条件,即其对偶问题与原问题是强对偶关系。
但需要注意 Slater 条件是强对偶的充分条件。
线性规划问题一定是强对偶;
二次规划问题一定是强对偶;
二次约束二次规划问题一定是强对偶(KKT 条件的关键)。