最优化方法——线搜索技术

最优化方法

线搜索技术

线搜索技术，又称一维搜索技术，是指求解但变量函数的极小值，是多变量求解问题的一个特例，也是多变量求解问题的一部分（一般用于确定步长 \(\alpha_k\)）。

下降方向我们一般以最速下降法为例，显然 \(d_k\) 就是梯度的负方向，是好寻找的，那么此时步长的寻找就很重要了。

我们想要取得一个步长 \(\alpha_k\) 使得下降速度快，即令 \[ \varphi(\alpha)=f(x_k+\alpha d_k) \] 使得 \[ \varphi(\alpha)<\varphi(0) \] 这使得选取的步长能够使得下降速度快，这也是一维搜索问题。

精确线搜索

精确线搜索主打找到一个最快的下降速度，即使得 \(\varphi(\alpha)\) 是最小值，这样下降速度就足够快。

此时我们不妨直接对其求导，得到 \[ \varphi'(\alpha)=\nabla f(x_k+\alpha d_k)^Td_k \] 如果方程简单，我们直接解方程即可；如果方程不简单，我们可以用数值方法求得近似解。

例如求解函数 \[ f(\mathrm{x})=2x_1^2+x_2^2\newline \mathrm{x}_1=(1,1)'\newline \epsilon=\frac{1}{10} \] 求解精确步长 \(\alpha_1\)。

首先可以求得函数的梯度为 \[ \nabla f(\mathrm{x})=\begin{bmatrix} 4x_1\\ 2x_2 \end{bmatrix} \] 那么下降方向为 \[ \mathrm{d}_1=-\nabla f(\mathrm{x}_1)=\begin{bmatrix} -4\\ -2 \end{bmatrix}\newline \|\mathrm{d}_1\|=2\sqrt{5}>\frac{1}{10} \] 建立函数 \[ \begin{align} \varphi(\alpha)&=f(\mathrm{x}_1+\alpha\mathrm{d}_1)\\ &=f(\begin{bmatrix} 1\\ 1 \end{bmatrix}+\alpha\begin{bmatrix} -4\\ -2 \end{bmatrix})\\ &=f(\begin{bmatrix} 1-4\alpha\\ 1-2\alpha \end{bmatrix})\\ &=2(1-4\alpha)^2+(1-2\alpha)^2 \end{align} \] 求导可得 \[ \varphi'(\alpha)=-16(1-4\alpha)-4(1-2\alpha) \] 由 \(\varphi'(\alpha)=0\) 求得 \[ \alpha_1=\frac{5}{18} \] 故迭代后，有 \[ \mathrm{x}_2=\mathrm{x}_1+\alpha_1\mathrm{d}_1=\begin{bmatrix} -\frac{1}{9}\\ \frac{4}{9} \end{bmatrix} \]

非精确线搜索

但是我们考虑到，每次都要进行求导运算的话，（解导数方程的）计算量是很大的，同时在距离最优解尚远时，并不需要下降速度最快，我们只需要下降速度较快即可。

但是不同的步长，也会使得迭代次数不同，如下图所示（由 \(\eta\) 表示步长）：

迭代次数与步长的关系

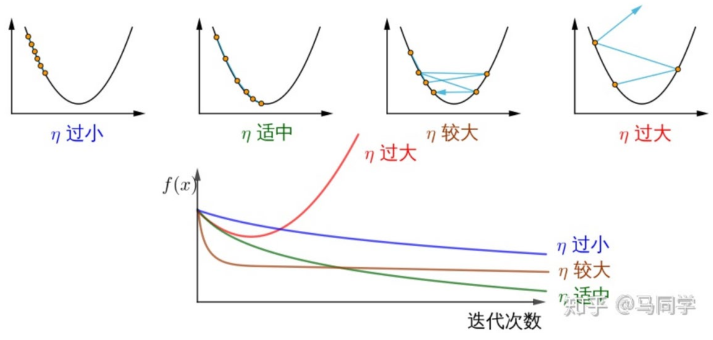
所以，即使是非精确的步长选取，也不能乱选。

最通用的非精确线搜索算法是 Armijo 准则。

Armijo 准则

给定一个 \(\beta\in(0,1),\sigma\in(0,0.5)\)，令步长因子为 \(\alpha_k=\beta^{m_k}\)，其中 \(m_k\) 是满足下列不等式的最小非负整数 \[ f(\mathrm{x}_k+\beta^{m}\mathrm{d}_k)\leq f(\mathrm{x}_k)+\sigma \beta^m \nabla f(\mathrm{x}_k)^T\mathrm{d}_k \] 一般来说，我们令 \(m=0\) 开始，逐步自增，直到满足上式条件后结束迭代。

算法的优势是不需要解方程，仅需要少量迭代就可以找到合适的步长。

比如说问题 \[ f(\mathrm{x})=\frac{1}{2}x_1^2+x_2^2\newline \mathrm{x}_0=(1,1)',\mathrm{d}_0=(1,-1)'\newline \beta=0.5,\sigma=0.9 \] 先求梯度，得到 \[ \begin{align} \nabla f(\mathrm{x}_0)&=\begin{bmatrix} x_1\\ 2x_2 \end{bmatrix}\newline &=\begin{bmatrix} 1\\ 2 \end{bmatrix} \end{align} \] 那么 \[ \nabla f(\mathrm{x}_0)^T\mathrm{d}_0=-1<0 \] 那么可以确定，\(\mathrm{d}_0\) 是函数在 \(\mathrm{x}_0\) 的一个下降方向。

那么 Armijo 准则的条件式化简为 \[ f(\begin{bmatrix} 1\\ 1 \end{bmatrix}+\alpha\begin{bmatrix} 1\\ -1 \end{bmatrix})=\frac{1}{2}(1+\alpha)^2+(1-\alpha)^2\leq \frac{3}{2}-0.9\alpha \] 即 \[ \frac{3}{2}\alpha^2-0.1\alpha\leq 0 \] 解得 \[ \alpha\leq\frac{1}{15} \] 那么尝试求解近似解，当 \(m=4\) 时，满足 \[ \alpha=0.5^4=0.0625\leq\frac{1}{15} \]