格密码相关笔记

发表于 2022-09-27 更新于 2024-03-19 本文字数： 20k 阅读时长 ≈ 18 分钟

有关格密码的简要笔记

格简介(Lattice)

给定一组线性无关的基向量 (basis) \((v_1,v_2,\cdots,v_n)\)，这些基向量的线性组合 (linear combinations) 为： \[ a_1v_1+a_2v_2+\cdots+a_nv_n,a_i\in R \] 而这些线性组合所组成的集合，称作这组基向量所张成的空间 (span)，也被称作向量空间。

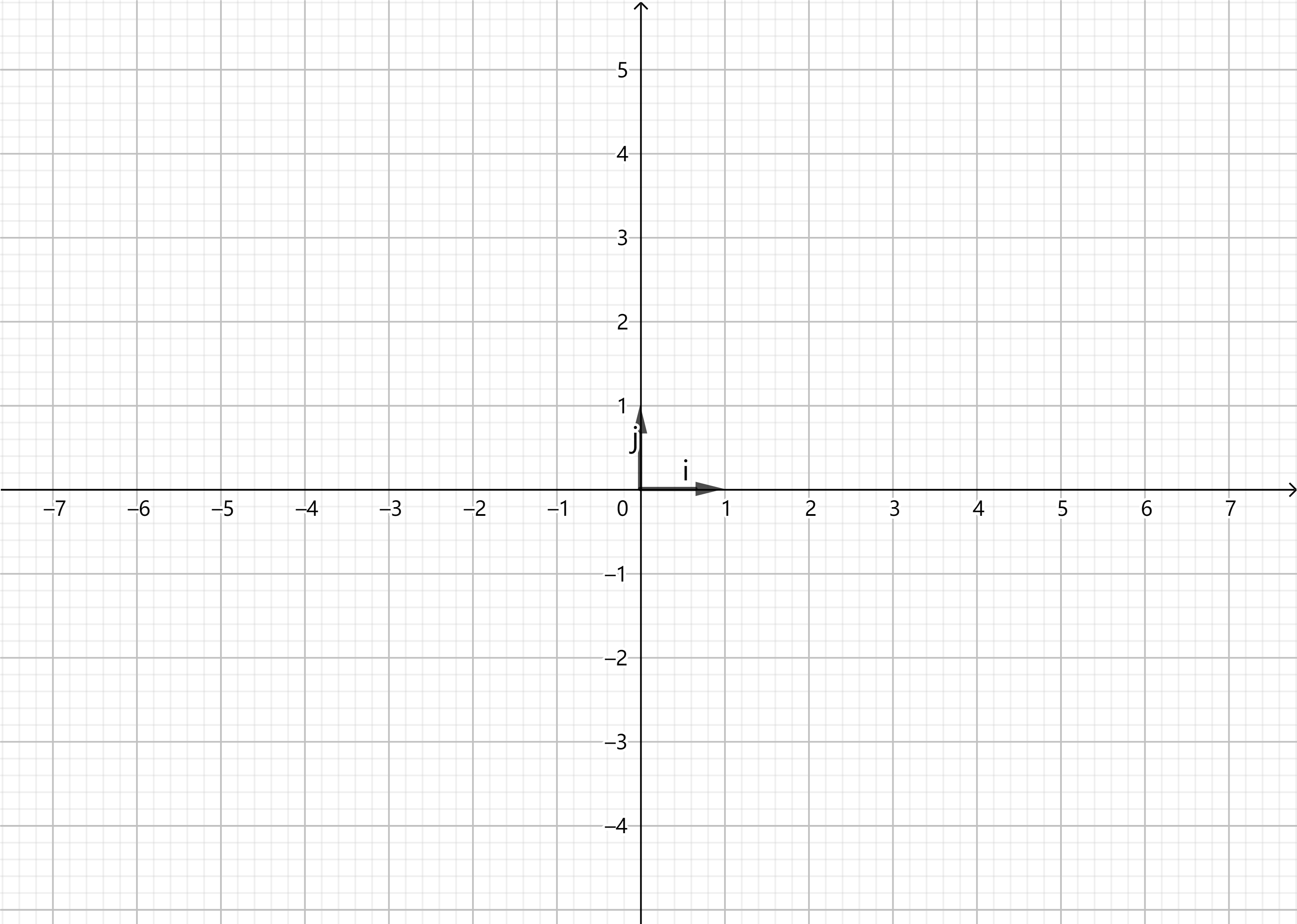
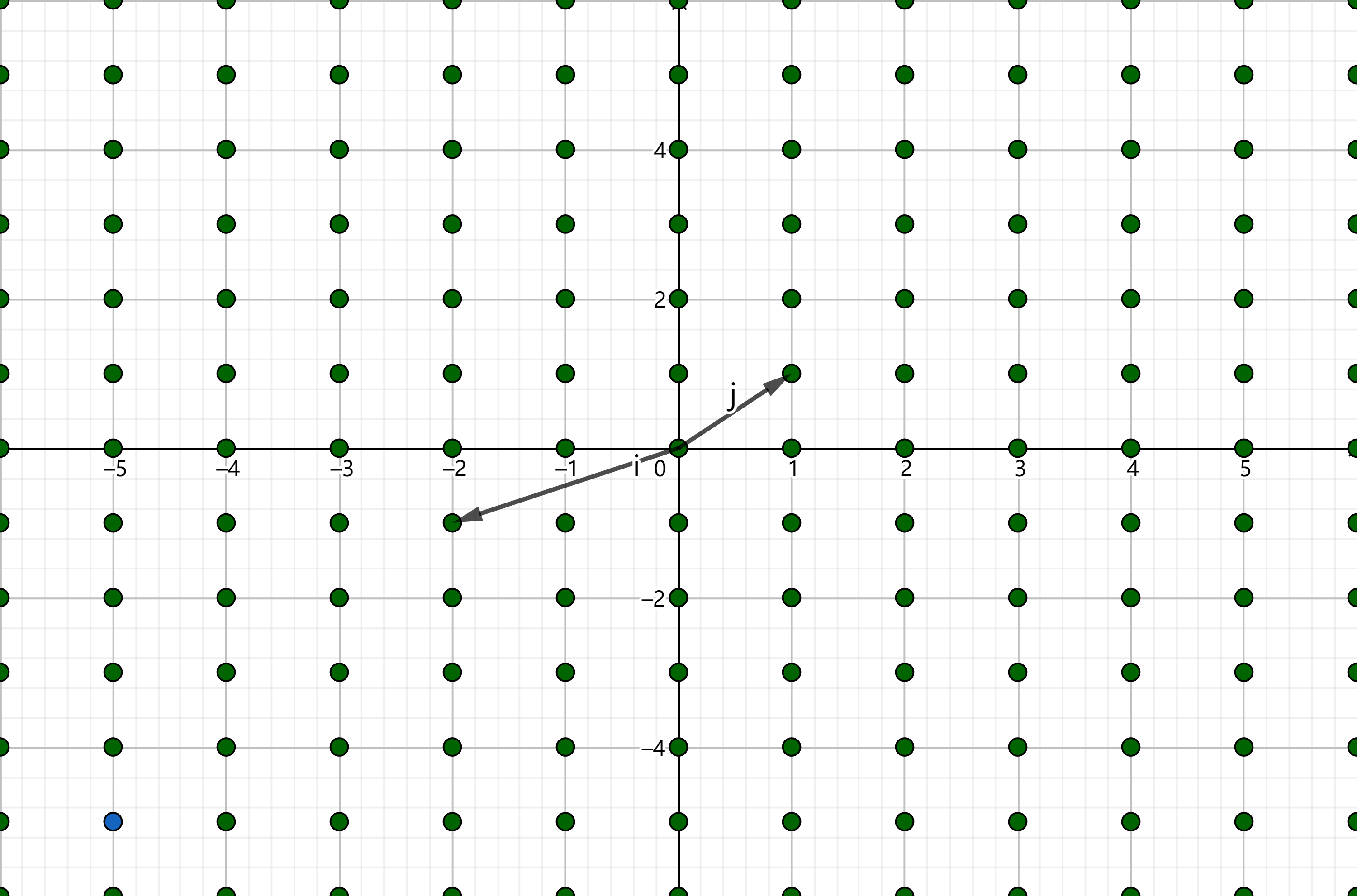
例如我们在二维平面中选取两个单位正交向量作为基向量： \[ i=(1,0),j=(0,1) \] 那么由这两组基向量组成的所有可能的线性组合为： \[ a\cdot i+b\cdot j=(a,b) \] 其中 \(a,b\in R\)，其所张成的空间便是整个二维平面。

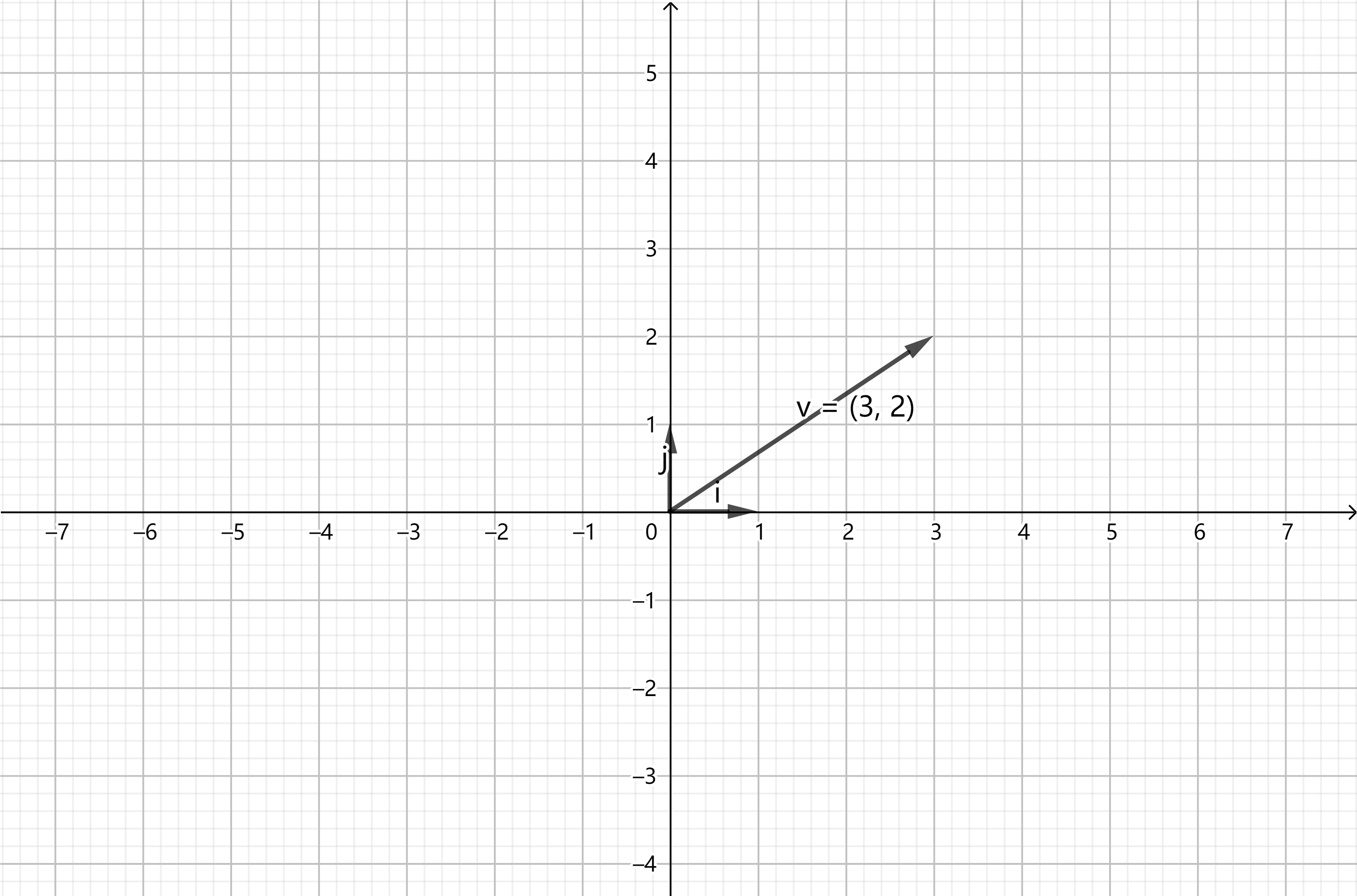
反过来，在这个二维平面上的任意一点都可以由这两个基向量的一个线性组合表示：

而格，就是这些基向量的所有整系数的线性组合： \[ a_1v_1+a_2v_2+\cdots+a_nv_n,a_i\in Z \] 这些线性组合所形成的集合就叫做这组基向量所张成的格 (lattice)，可以简单理解为离散的向量空间。

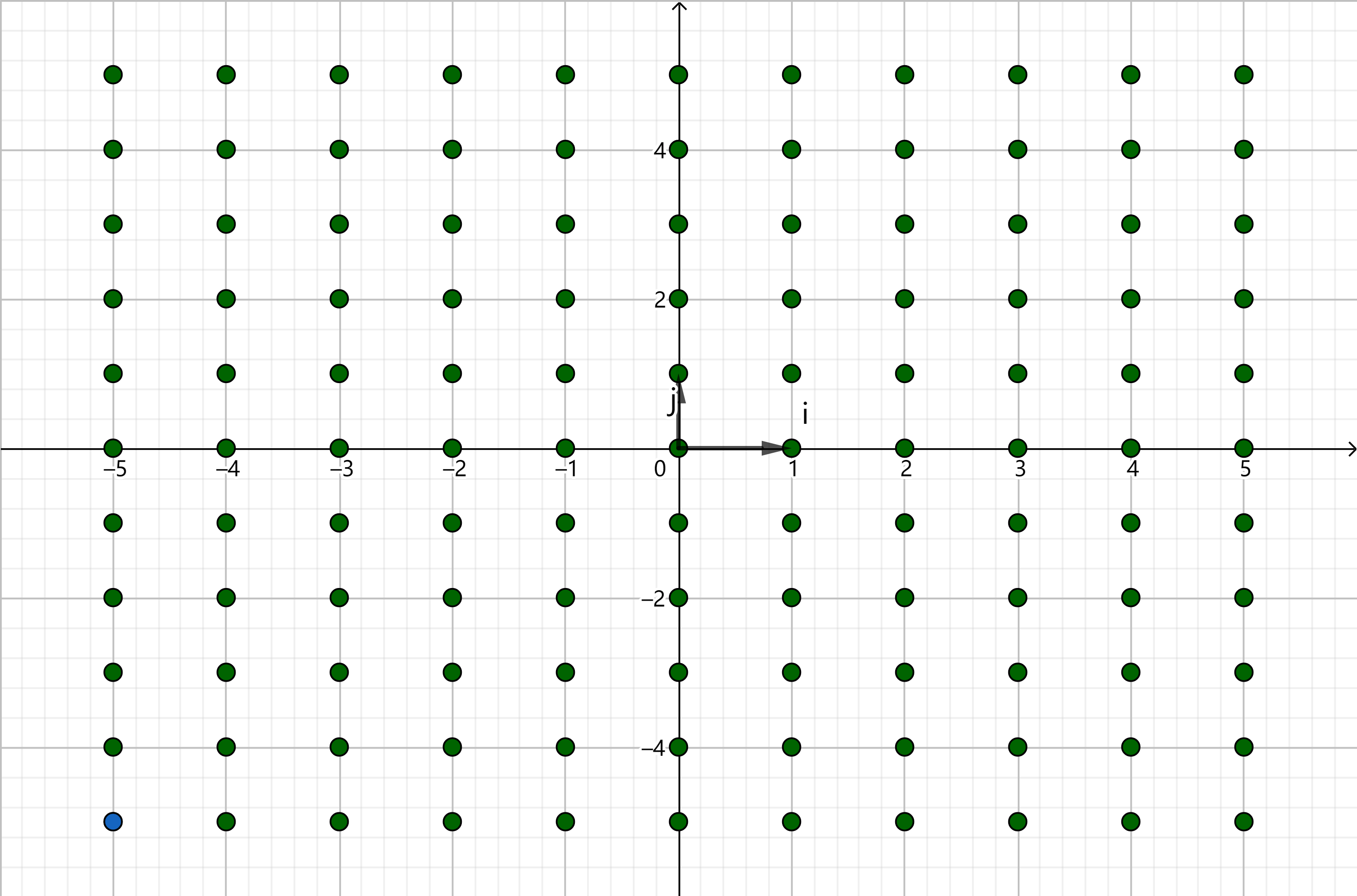
当系数不是实数而是任意整数的时候，其所张成的线性空间从无数个连续的点变成了无数个离散的点。

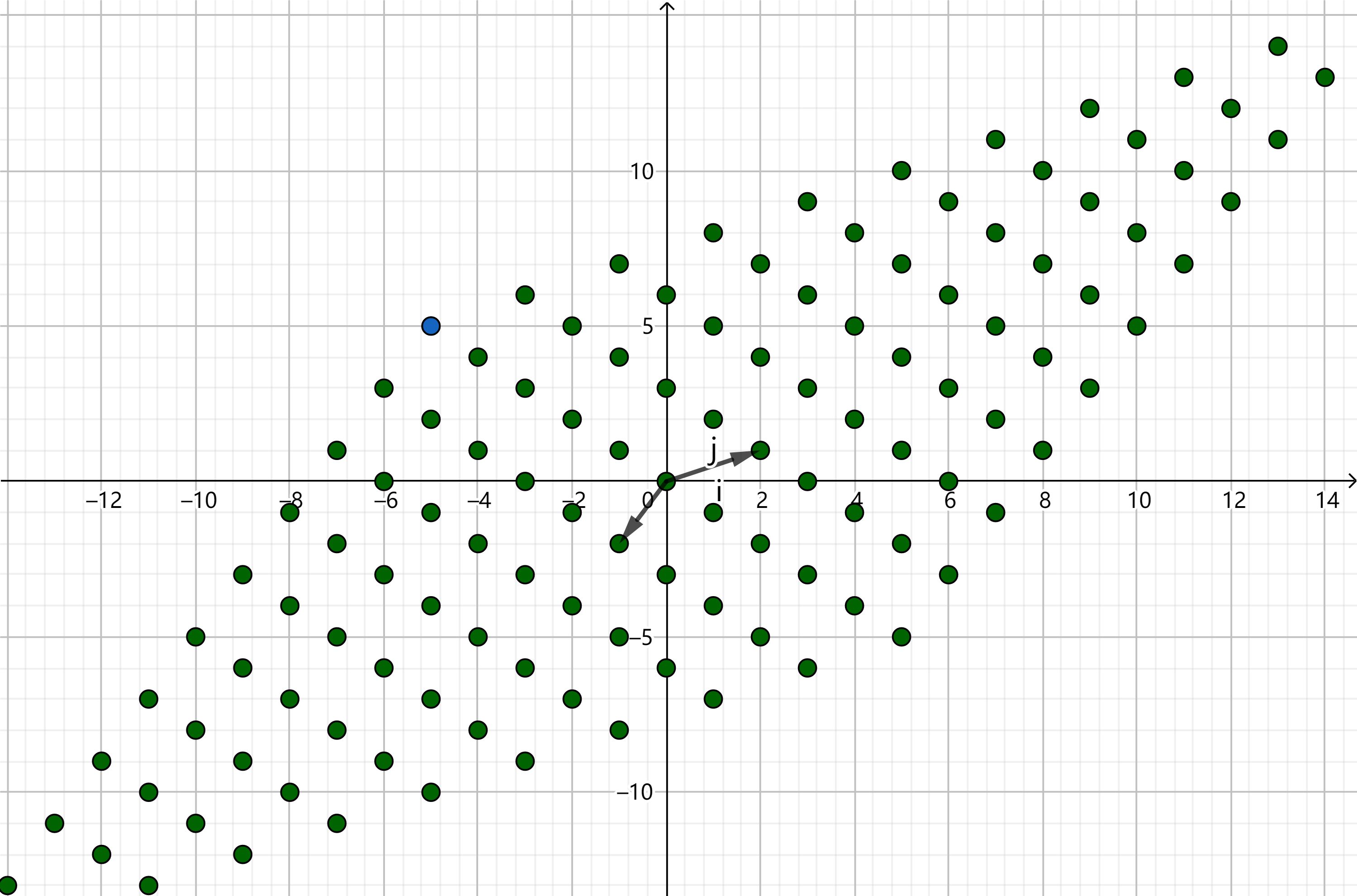
当基向量发生改变时，其所张成的格也会发生改变：

如果对原基底进行整系数线性变换，得到的新基底所张成的格仍旧不变：

所以我们可以发现，就算是同一个格，也可以有很多组基底。

而在格学说里，有两个知名难题：

SVP (最短向量问题，Shortest Vector Problem)：给定lattice和基向量，找到lattice中的一个长度最短的非零向量。
CVP (最近向量问题，Closest Vector Problem)：给定lattice和基向量，以及一个不在lattice上的目标向量，找到lattice中一个距离目标向量最近的格向量。

在广义上这两大难题被证明是 NP-hard 问题。

小格可以使用 Sagemath 的 LLL 算法求解格规约，但大格可能 Sagemath 提供的算法效率不够，这个时候可以借助 flatter 库进行格规约计算。

M = matrix(ZZ, [(66586820,65354729),(6513996,6393464)])
def flatter(M):
    from subprocess import check_output
    import re
    inputM = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    outputM = check_output(["flatter"], input=inputM.encode())
    return matrix(M.nrows(), M.ncols(), map(int, findall(b"-?\\d+", outputM)))
flatter(M)

格规约

在格学说中，通常要运用格规约算法去解决某些问题，而格规约算法实际上就是求解格中最短基的算法。

考虑一个格可以由不同的基底组成，但比如说二维格可以由多个基底向量构成，比如说 \[ \begin{bmatrix} 1&3\newline 2&4\newline 3&9\newline \end{bmatrix} \] 但是我们考虑到，实际上我们并不需要那么多的向量去描述一个格，类似于线性代数中满秩或无关向量组的概念，有一些向量可能是无用的，这个时候我们可以将其摘除 \[ \begin{bmatrix} 1&3\newline 2&4\newline \end{bmatrix} \] 但有时候我们会觉得一组基底不够好，可以由一组更短的基底来描述这个格，类似于 GCD 算法，通常我们也会对不同的向量之间作规约计算，可以得到一组更短的基底来描述格 \[ \begin{bmatrix} 1&1\newline -1&1\newline \end{bmatrix} \] 这是因为 \[ (1,3)=2(1,1)+(-1,1)\\ (2,4)=3(1,1)+(-1,1) \] 显然，新的基底向量更短（指范数大小）。

在线性代数中，对一组基底进行线性变换，就是作矩阵乘法，得到新的向量。在格学说中，也是一致的。

格对密码学研究的帮助是，如果我们可以证明解向量是格中的最短基底向量之一，那么我们就可以用格规约算法对格进行运算，从而避免系数矩阵（线性变换）直接求得解向量，例如 \[ \mathcal{L}=\begin{bmatrix} 1&3\newline 2&4 \end{bmatrix}\\ (x_0,x_1)\mathcal{L}=(y_0,y_1) \] 只需证明 \[ \|(y_0,y_1)\|\leq \sqrt{n}|\det{(\mathcal{L})}|^{1/n} \] 其中，\(n\) 是格的维度，那么就可以说明解向量是格的最短基底向量之一，即 \[ \bold{y}=(1,1)\text{ or }\bold{y}=(-1,1) \] 这也就是 SVP 问题。

上文使用了赫米特定理，即对于所有 \(n\) 维的格 \(\mathcal{L}\)，都包含一个非零向量 \(v\in \mathcal{L}\) 满足 \[ v\leq \sqrt{n}|\det{(\mathcal{L})}|^{1/n} \] 除此之外还有更精确的高斯启发式（The Gaussian Heuristic）。

如果 \(\mathcal{L}\) 是 \(n\) 维的格，那么最短基底向量的长度是 \[ \|v\|\approx \sigma(\mathcal{L})=\sqrt{\frac{n}{2\pi e}}|\det{(\mathcal{L})}|^{1/n} \]

格规约算法有许多，最常见的是 LLL 算法，但 LLL 算法得到的基向量质量不一定完美，可能还需要使用 BKZ 算法进行调整。

SVP 问题

虽然说 SVP 是 NP-hard 问题，但当维度较低时，存在 LLL 算法可以在多项式时间内求解 SVP 问题。

SVP 问题可以简化成如下表达式： \[ f\cdot h\equiv g\pmod{p} \] 其中所有变量都为整数，\((h,p)\) 为已知向量，此时需要满足 \(||(f,g)||\) 的长度较小，使得该向量为这个格的最短向量，即可转换为 SVP 问题求解 \((f,p)\) 向量。

我们构造矩阵 \(M\) 为： \[ M=\begin{bmatrix} 1&h\\ 0&p \end{bmatrix} \]

证明：向量 \((f,g)\) 是在该格上。

首先将同余式变形为 \[ f\cdot h\equiv g+k\cdot p \] 即 \[ f\cdot h-k\cdot p\equiv g \] 我们可以发现 \[ \begin{align*} (f,-k)\cdot M&=(f,-k)\begin{bmatrix} 1&h\\ 0&p \end{bmatrix}\\ &=(f+0,f\cdot h+(-k)\cdot p)\\ &=(f,f\cdot h-k\cdot p)\\ &=(f,g) \end{align*} \] 向量 \((f,g)\) 可以由基向量 \(M\) 的某种整系数线性组合 \((f, -k)\) 来表示，因此向量 \((f,g)\) 就在这个格上。

之后我们只需要使用 LLL 算法即可。

一个可能的代码示例（使用 Sagemath）：

1 2	M = matrix(ZZ, [(66586820,65354729),(6513996,6393464)]) shortest_vector = M.LLL()[0]

SSP 问题

SSP 问题，即子集和问题(Subset Sum Problem)，针对的是形如 \[ s=w_1x_1+w_2x_2+\cdots+w_nx_n \] 的方程，已知权重向量 \(\bold{w}=(w_1,\cdots,w_n)\) 和结果 \(s\)，求解 \(\bold{x}=(x_1,\cdots,x_n)\)，其中 \(x_i\in \{-1,0,1\}\)，主要针对的是背包密码 Knapsack。

普通子集和问题

原理

针对方程 \[ s=w_1x_1+w_2x_2+\cdots+w_nx_n \] 可以改写成 \[ \bold{x}\bold{w}^T=s \] 考虑扩写 \(\bold{x}\)，使得方程变为 \[ \mathcal{B}=\begin{bmatrix} 1&&&&w_1\newline &1&&&w_2\newline &&\ddots&&\vdots\newline &&&1&w_n\newline &&&&s \end{bmatrix}\newline (x_1,\cdots,x_n,-1)\mathcal{B}=(x_1,\cdots,x_n,0) \] 为了使解向量更小，使得其在格内，考虑构造为 \[ \mathcal{L}=\begin{bmatrix} 1&&&&Nw_1\newline &1&&&Nw_2\newline &&\ddots&&\vdots\newline &&&1&Nw_n\newline \frac{1}{2}&\frac{1}{2}&\cdots&\frac{1}{2}&Ns \end{bmatrix} \] 其中，\(N>\sqrt{n}\)，这样使得解向量为 \(\bold{x}'=(x_1-\frac{1}{2},\cdots,x_n-\frac{1}{2},0)\)，满足 \(\|\bold{x}'\|=\frac{1}{2}\sqrt{n}\)。

即可以写成 \[ \mathcal{L}=\begin{bmatrix} \mathrm{I}&N\cdot\mathrm{W}\\ \frac{1}{2}&Ns \end{bmatrix} \] 其中，\(\mathrm{W}=(w_1,\cdots,w_n)^T\)。

要求密度满足 \[ d=\frac{n}{\log_2\max{w_i}}<0.9408 \]

代码

使用 sagemath 实现，基底向量可能会为 \(-\bold{x}'\)

w = [83, 59, 47, 81, 76, 51]
s = 291
n = len(w)
N = ceil(sqrt(n))
W = matrix(w)
E = identity_matrix(ZZ, n)
L = block_matrix([[E, N * W.T], [ones_matrix(1, n) / 2, N * s]])
M = L.LLL()
x1 = M[0][:n].apply_map(lambda x: x + QQ(1/2))
x2 = M[0][:n].apply_map(lambda x: QQ(1/2) - x)
x1, x2

扩展子集和问题

针对更多的约束，我们可以扩展格。

MSSP 问题

MSSP，多子集和问题，Multiple Subset Sum Problem。

形如 \[ (x_0,\cdots,x_n)\begin{bmatrix} w_{1,1}&\cdots&w_{1,k}\\ \vdots&\ddots&\vdots\\ w_{n,1}&\cdots&w_{n,k} \end{bmatrix}=(s_1,\cdots,s_k) \] 扩展普通 SSP 问题的格为 \[ \mathcal{L}=\begin{bmatrix} \mathrm{I}&0&N\cdot\mathrm{W}\\ \frac{1}{2}&\frac{1}{2}&N\cdot\mathrm{S} \end{bmatrix} \] 其中，\(W\) 为权重矩阵，\(S\) 为子集和向量，\(N>\sqrt{\frac{n+1}{4}}\)。

要求密度满足 \[ d=\frac{n}{k\log_2\max{w_{i,j}}}<0.9408 \]

其中解向量为 \[ (x_1-\frac{1}{2},\cdots,x_k-\frac{1}{2},-\frac{1}{2},0,\dots,0) \]

MMSSP 问题

基于模子集和问题，Modular Subset Sum Problem，即 \[ s=w_1x_1+w_2x_2+\cdots+w_nx_n\pmod{M} \] 扩展为多模子集和问题，Multiple Modular Subset Sum Problem，即 \[ (x_0,\cdots,x_n)\begin{bmatrix} w_{1,1}&\cdots&w_{1,k}\\ \vdots&\ddots&\vdots\\ w_{n,1}&\cdots&w_{n,k} \end{bmatrix}=(s_1,\cdots,s_k)\pmod{N} \] 扩展 MSSP 问题的格为 \[ \mathcal{L}=\begin{bmatrix} \mathrm{I}&0&N\cdot\mathrm{W}\\ &&N\cdot M\cdot\mathrm{I}\\ \frac{1}{2}&\frac{1}{2}&N\cdot\mathrm{S} \end{bmatrix} \]

要求密度满足 \[ d=\frac{n}{k\log_2\max{w_{i,j}}}<0.9408 \]

其中，\(W\) 为权重矩阵，\(S\) 为子集和向量，\(N>\sqrt{\frac{n+1}{4}}\)。

其中解向量为 \[ (x_1-\frac{1}{2},\cdots,x_k-\frac{1}{2},-\frac{1}{2},0,\dots,0) \]

LWE 问题

原理

LWE 问题，即 Learning-with-errors 问题，针对的是形如 \[ \boldsymbol{S}=\boldsymbol{R}\cdot x+\boldsymbol{E} \] 的方程组，即 \[ \begin{cases} s_1=r_1\cdot x+e_1\\ s_2=r_2\cdot x+e_2\\ \ \ \ \ \ \ \vdots\\ s_n=r_n\cdot x+e_n\\ \end{cases} \] 其中 \(e_i\) 我们称作误差（error），是未知量，而 \(r_i,s_i\) 为已知量，对这个方程组求解 \(x\) 即 LWE 问题。

这在深度学习领域是一个重要问题，即每次的输入和输出有一定的误差存在，要如何根据输出求解输入。

代码

p = 6897108443075981744484758716081045417854227543713106404294789655180105457499042179717447342593790180943415014044830872925165163457476209819356694244840079
rs = [12844634549263053228759749264403637022740290008286987401585068952741935277415527678380021212624846722242500708422759563558995936977274580301379494195702461, 12251634003683452916928102291170339939586644029776192301741341674585154859358419625191986830852794085541953563738986709807899575511700135958334229151930861, 7051370666077542197248638013011793824477073777322219545882367881807130066168444134964571398112151848834032654978368255218649720738040945429837692857031957, 9773046862351952930368505593284546267554571295872377323111558071278701231472975791962979256551519533723988556870551885073742407630481198192389750289392107, 8883776497660138308720006912582738672888752344326928153810910221453595077711284302041512529457450211602787210761461172326429880594024187025419873043435877, 12056735137145460036580841038332100311160368843873164649606343042416896898793233249873902218683966283969721460087390120622254758027779960740926123005377571, 8819958747150954554494406068232243249186433676383469322817152210037563032056202909377825740775383087605647374150477096718956454225946093710691864988563109, 12246023449098354751049599873213988024512286270964608502444597112110163392131757813461977030270733012385926751192637938686124570227538910606279104888073013, 11308837998867241929817950595621831002334468993828126438599805989088017326675963100044309448653090403889186401929445861220402556074702741108929442867300279, 9184622887414209361516593101129556569811888214607556630094969763910426953786020755838094184972397480276666170685926425137063559394969166216392939257091541, 12896400069515890897430087815982545671830645201023665112429779640768899091287291452408369445919464144390726200808875066389240126909811239597092893733457339, 11227025698697471809912850435140886785315702278826761054472525227951791647003561270585720797267604996360933395122286757099101227901032364782594523739698877, 8162123490656317490361880020667919072708091053716891870691544217490126444997503404094174246087938828993696335191488583306443577208796794274099282013427247, 13366989889442670291461262313757977600095962057470863475519088648267301129719953368943419562144276679400967122727554764013132918505564677243979978807323041, 9920857455945408588203972193444437533164351309299040911469275059092031755811492460585653948481522995557801781838215407648572999358456612525812067538372579, 7139402473546047825312503780125417567716958846513076797328672521987900978293260385267945187604725349720103672258987935569856239987227455748213833342843243, 13108142660294572752252393081421368493392921884487755391460006730258159004638343897340537616297811742032405724656497443006056456690449881719305597286675631, 13276762958403786077380090195631980415297280849950287990717193547481553124160398455403123819234755237450529090601858784999113026218918277529515287668651121, 12463094640052886550696551772104539361264529587569204472038955376345085195998921095774583176899949596998985033050547755235409943131811058035802010421860899, 11307743131694864808301935844724645695851330736969875190167422024500753079857478680029193758960169072890576310607053767920339034290416580654771095674487943, 10053742503547378455068966704402695956702795408343604912294923217443553169726438945982031485796964462946592530592946335569560364464958066521486506177193131, 9703695763451799125258961776229325510814289358679213305418559381901496449849584244211834872313767844996255556721041007654625153809128987422992102292472533, 8148189465927721940294369879439913703690047528695196368949823197675716174991296513758196009346701553643721225250628151384047219921709201619262393792138023, 9114150910964237818418367840207724528917302406836157928223872622442928604249864486858755737149640683259834299165900696585038569188627682022002709058902291, 12273514376180781903469287345188404399033432117915094289694407562166649079228640510678711431664410226301556172582177240184695103942141430877677144285616059, 8355005721684425514882933910286584148305344580589623112959517428993968438533866906223777778058096962333203237111245328436600994120168924143849685728268811, 8957883838807471492147480816683526636019698464133185237668243268667169800811696770484487123560197988448434475112352005768286417529319182162245840523697001, 12168542584724814356632409768687396920143300559579648963851924568387314914334359305942685551210180448419674060219496395116081866784918059237133414041227833, 12285935007930825571672128346804313607196190465690759870758278705086034778808662886056460827935986285259185071514490942831585313190946386878622608868345563, 7719913817859572377164973343651155934060296607908537845256755472465025202751239980758950094865067751407889569369974011139801401586939119147773466111699913]
cs = [3911325901261770731066343727353093385607196883601022244426857460074338420692610012414571623512152485474248169220030587839849722757773859682519433853455847, 4198555117325325874584019691418573071733167640213933749582347442518997588452211673143722179281773602455507001395983681009769848414007206268682184816168744, 4422173666634983234895098798813962037875417568235708524339826709271381748884936178371767574064794177416615710120223914725873239836121654705208614576413533, 3540260422555697887869627546208164711550015909378340105077652177481959576550678379723450981807556863572610759824660630418670546203733170058626755080797998, 6451498467498935201092514865627931677091078787997097414208430992183264950579022373372254486595458117887305393317663712337699331503725124287017134808484874, 3439629581963524351810430910737336124616316641656190641248434504621774235943514617301857917041111617104850245148746427180069743940612560718213177903427306, 4279468191481832212496939242093486044278976937965085475567008228061184947513156012369586970486543083130565628906296600553024574099481246534878242920637212, 4102135455518061133919027670571325279976222647984452353051395864554309521223498761823084717077102213648612826513661629599971609555235760152049549057234342, 329051927890365028889097463563711966673066795688728876214731188783168691555262156515161429328581094087585127929869064685419149676592073496155898360311360, 1674347209896897571502352451063188834938904430329951752111921115230349947823188121972980025563878887201507629419811736910690965020923751424101521816057970, 4779084317811375050159574994746297486592271247137823471375199626788956576998627181220489952507937768042501203098391966702297812537463211799837921684467541, 5240331815784322792144549873873658636726233093228415489098002982220769676718681132737794994708716389174162820721646744776624413735318240597745363490427584, 2689716894922604875455207695253665212853470308341743040957367957727155614199743562225147359614514189877983156892749669804800163252617480446565479990148021, 449708769594599088851244243076921016853502252396793496349534051273454215985560340288452398756880916680293627457774430655982228613348249480600180821975835, 1584603978331289335352997151059666773277943458357161051278658090420067023680231414255557805410288144092653121568766136372728095300982743309696347031121424, 4874260053151700374809337053763032489184725334196495160358275038586824027920238733886703163018450814805937363825223459277373073591021082276610135118976834, 3524374131362906900545297291947110177298862564718451821839794960169356082042548386553363480921097452902723033854749443288682983558847052843293666815425196, 6544123591499569232021913370293570477776709315008783531720886545784773471486769240711262562401683145937715612435213816372680189321141928790509490282629891, 4873861166228118967099569086478548167127431415017791678812419676791754466935832034870862000658789609084166891933970013849850146718379819943737269970654866, 4100817874436703071716655163972145036104985973164830547825929590871920825981241934633977227547934514142660786061291026657802357404024236287955309372489516, 343238276681348130286495167739162902430650061145485619903964358840996341335935043000395056684771452815629410388891486531126938900311458948803147120186532, 2683710724350412998770392318832434885304538325033159937379489319924346689197445720734209841902612235485016866254994045969716413020197296428323832404151182, 5909464641105704179999104311562416363090166762341644691188169716182958971270396007422581429813172933930581475771306034495224054972725230757675444731953480, 105593489999747649490909471306354863316673821363863362258853043970534652401274789197677558215188249074837829003335733211890211648501689656345824858507373, 4992379366542645691375959247465888889778118153982142100956809440855745659745235576280578316185469306620017845690312554043770651058126536040173113949524396, 6533456398244789907636779407045515567135195474284185379689518387558345997627435421582437390053234675991361808532278264077968540197407743744279106871716267, 5169360398767270275853790242315213671633880428212603766301308853363063092609582572957561138022806887895634140899640025570759919257615537375706008159680239, 203310740924699994885931266978520636166917734618272844754878785050509801614513144739164450834936178065792112797202959106365282699245578309060905297742706, 3143563289239398127009575193211845399079310618985464994769603542400451633289266080869317336163844517539211542909055869608349639432145332113320465388067087, 4016252180207572047405081190649590978593306403200098541033213590567723751195926093369984531729148621419589009515870336049849542537363832071754623330736088]
enc = 1315637864146686255246675143589215932218700984880749264689270214639479160648747323586062096067740047809798944996253169402675772469028914904598116394230426

#脚本1-小规模
#Sage
from sage.modules.free_module_integer import IntegerLattice

row = 30
column = 30
prime = p

ma = rs
res = cs

W = matrix(ZZ, ma)
cc = vector(ZZ, res)

# Babai's Nearest Plane algorithm
def Babai_closest_vector(M, G, target):
    small = target
    for _ in range(5):
        for i in reversed(range(M.nrows())):
            c = ((small * G[i]) / (G[i] * G[i])).round()
            small -=  M[i] * c
    return target - small

A1 = matrix.identity(column)
Ap = matrix.identity(row) * prime
B = block_matrix([[Ap], [W]])  
lattice = IntegerLattice(B, lll_reduce=True)
print("LLL done")
gram = lattice.reduced_basis.gram_schmidt()[0]
target = vector(ZZ, res)
re = Babai_closest_vector(lattice.reduced_basis, gram, target)
print("Closest Vector: {}".format(re))

R = IntegerModRing(prime)
M = Matrix(R, ma)
M = M.transpose()

ingredients = M.solve_right(re)
print("Ingredients: {}".format(ingredients))

HNP 问题

HNP 问题，即 Hidden Number Problem。

内容记录在另一篇文章里。

Noise

Noise CRT

噪声 CRT，指的是对正常的 CRT 矩阵 \[ A=\begin{bmatrix} N_1\pmod{p_0}&N_2\pmod{p_0}&\cdots&N_n\pmod{p_0}\\ N_1\pmod{p_1}&N_2\pmod{p_1}&\cdots&N_n\pmod{p_1}\\ \vdots&\vdots&\vdots&\vdots\\ N_1\pmod{p_m}&N_2\pmod{p_m}&\cdots&N_b\pmod{p_m}\\ \end{bmatrix} \] 每一行进行置乱（噪声污染），那么对这种被噪声污染的 CRT 矩阵，已知 \((p_0,\cdots,_n)\) 和噪声结果 \(S_{n\times m}\) 如何还原 \((N_1,\cdots,N_n)\) 是主要研究问题。

一个可能的生成噪声 CRT 矩阵的代码如下

N = [getRandomNBitInteger(3211) for _ in range(15)]

def leak(N):
    p,S = [],[]
    for i in range(15):
        p.append(getPrime(321))
        r = [N[_]%p[i] for _ in range(15)]
        shuffle(r)
        S.append(r)
    return p, S

p, S = leak(N)

解决代码如下

m = 15
nbits = 3211
P = prod(p)
Ti = []
for i, pi in enumerate(p):
    Pi = P // pi
    invPi = inverse_mod(Pi, pi)
    Ti.extend(S[i][j] * Pi * invPi for j in range(m))
T = column_matrix(Ti)
B = diagonal_matrix([2^nbits] * len(Ti))
M = block_matrix([[matrix([P]), 0], [T, B]])
def flatter(M):
    from subprocess import check_output
    import re
    inputM = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    outputM = check_output(["flatter"], input=inputM.encode())
    return matrix(M.nrows(), M.ncols(), map(int, findall(b"-?\\d+", outputM)))

flatter(M)

Hash

线性 Hash

def hash(msg: bytes):
    n = 30798082519452208630254982405300548841337042015746308462162479889627080155514391987610153873334549377764946092629701
    g = 91289086035117540959154051117940771730039965839291520308840839624996039016929
    N = 2 ** 100
    for mi in msg:
        n = g * (2 * n + mi) % N
    return (n - 0xdeedbeef114514) % N

考虑这个哈希算法全是线性操作，用 \(m_i\) 表示每个字节，仅考虑 \(n_{i+1}=2gn_i+g\cdot m_i\) 且 \(n_0\) 存在，那么可以展开得到 \[ \begin{align} n_{i+1}&=(2g)^{i+1}n_0+(2g)^ig\cdot m_0+(2g)^{i-1}g\cdot m_1+\cdots+(2g)^0g\cdot m_{i}\pmod{N}\\ &=(2g)^{i+1}n_0+\sum^{i}_{k=0}(2g)^{i-k}g\cdot m_k \end{align} \] 要进行碰撞两个相同哈希值但不同的字节流，不妨设两个字节流分别为 \((s_0,\cdots,s_i),(t_0,\cdots,t_i)\)，即可以表示为 \[ \begin{align} n_{i+1}&=(2g)^{i+1}n_0+\sum^{i}_{k=0}(2g)^{i-k}g\cdot s_k\pmod{N}\\ &=(2g)^{i+1}n_0+\sum^{i}_{k=0}(2g)^{i-k}g\cdot t_k\pmod{N} \end{align} \] 等式左右两边相减可得 \[ \sum^{i}_{k=0}(2g)^{i-k}g\cdot (s_k-t_k)\equiv 0\pmod{N} \] 不妨令 \(e_k=s_k-t_k\)，可以构建矩阵 \[ R=\begin{bmatrix} (2g)^ig\\ (2g)^{i-1}g\\ \vdots\\ (2g)^0g \end{bmatrix} \] 满足 \[ (e_0,e_1,\cdots,e_i,k)\begin{bmatrix} R\\ N \end{bmatrix}=0 \] 这里的 \(k\) 是同余方程的常系数。

那么可以构建格规约 \[ M=\begin{bmatrix} 1&0&\cdots&0&(2g)^ig\\ 0&1&\cdots&0&(2g)^{i-1}g\\ \vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&1&(2g)^0g\\ 0&0&0&0&N \end{bmatrix} \] 可以证明解向量 \((e_0,e_1,\cdots,e_i,0)\) 在格内。

格中最后一个元素为 \(0\) 的向量即是我们想要寻找的向量。

n = 30798082519452208630254982405300548841337042015746308462162479889627080155514391987610153873334549377764946092629701
g = 91289086035117540959154051117940771730039965839291520308840839624996039016929
N = 2 ** 100
msize = 33

R = [(2 * g) ** (i) * g for i in range(msize)]
R = column_matrix(R[::-1]) % N
E = identity_matrix(msize)
M = block_matrix([[E, R], [0, matrix([N])]])
X = M.LLL()
sbytes = b'a' * msize
print(sbytes, hash(sbytes))
tbytes = list(b'a' * msize)
for i in range(msize):
    tbytes[i] -= X[2][i]
tbytes = bytes(tbytes)
print(tbytes, hash(tbytes))
"""
b'aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa' 842280076996392056218680371307
b'bdabdefd]]\\`[cbb^b]dfcc_\\`bda\\caa' 842280076996392056218680371307
"""