DES 算法笔记
DES 算法简述
DES算法是一种最通用的对称密钥算法,因为算法本身是公开的,所以其安全性在于密钥的安全性。基于密钥的算法通常有两类:对称算法和公开密钥算法。对称算法的对称性体现在加密密钥能够从解密密钥推算出来,反之亦然。在大多数对称算法中,加解密的密钥是相同的,DES就是这样。可见,对称密钥算法的加解密密钥都是保密的。而公开密钥算法的加密密钥是公开的,解密密钥是保密的。
下面是 DES 加密算法的整体流程图:
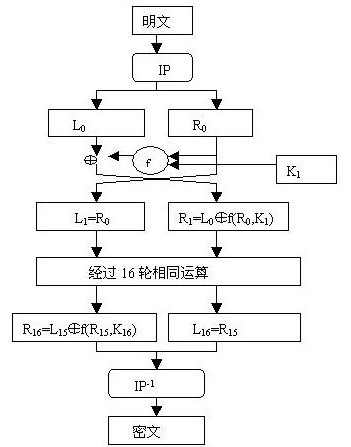
从流程图中可以看出,DES 明显基于 Feistel 密码结构,其中 f 为轮函数。
并且需要注意到,事实上密钥只有 56bits 参与了 DES 算法(其中第8、16、24、32、40、48、56、64位是校验位,使得每个密钥都有奇数个 1),分组后的明文组和56位的密钥按位替代或交换的方法形成密文组。
DES 算法描述
初始置换 \(IP\)
将输入的 64bits 明文重新进行排序,即将第 58 位放到第 1 位,第 50 位放到第 2 位,并且以此类推,最终有一个 8x8 的置换表如下:
1 | // 初始置换表 IP |
置换后,\(L_0\) 为新数据的左 32bits,\(R_0\) 为新数据的右 32bits,即分为高、低32位。
密钥置换 (子密钥 \(K_i\) 的获取)
密钥置换将从原始的 56 位密钥中得到 16 个子密钥 (轮密钥) \(k_i\),其中每个子密钥 \(k_i\) 都是 48 位。
首先注意到 DES 的输入密钥通常是 64 位,其中每第 8 个位都作为前面 7 位的一个奇校验位。但校验位并不会增加密码安全性,所以因为此可以说 DES 的密钥是 56 位的,而不是 64 位的。
于是首先我们需要通过忽略所有第 8 位的方式将 64 位密钥缩短为 56 位。示意图如下:
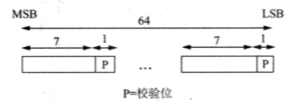
而置乱使用的表如下:
1 | // 密钥置换表,将64位密钥压缩为56位 |
以上被称为第一次置换。
然后要将得到的 56 位密钥将分为 \(C_0\) 和 \(D_0\) 两部分,同时长度均为 28 位的左右两部分将周期性地向左移动一位或两位 (即循环移位),而移动的具体位数取决于轮数 \(i\),规则如下:
- 在第 \(i=1,2,9,16\) 轮中,左右两部分向左移动一位
- 在 \(i\neq 1,2,9,16\) 的其他轮种,左右两部分向左移动两位
循环移动的位置的总数位 \(4·1+12·2=28\),这将带来一个有趣的属性,即 \(C_0=C_{16}\) 和 \(D_0=D_{16}\)。而这对解密密钥编排 (其中子密钥都是逆序生成的) 非常有用。
\(k_i\) 的第二次置换过程图如下:
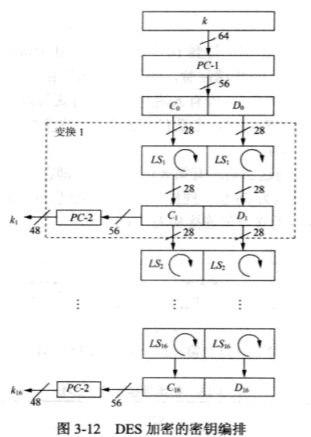
例如对于 01010111 循环移位两位的结果为 01011101
为了得到 48 位的轮密钥 \(k_i\),左右两部分需要再次进行压缩置换 (第二次置换)。
因为这个过程中,即置换了每位的顺序,又选择了子密钥,因此称为压缩置换 (注意表中没有 9,18,22,25,35,38,43 和 54 共八位)。压缩置换表如下:
1 | // 压缩置换,将56位密钥压缩为48位子密钥 |
同时每轮左移的位数如下:
1 | // 每轮左移的位数 |
最后通过不断的左移后压缩置换,我们依次得到了 \(k_1,k_2\cdots k_{16}\)。(上一次的输出为下一次的输入)
轮函数 \(f\)
在第 \(i\) 轮种,\(f\) 函数的输入为前一轮输出的右半部分 \(R_{i-1}\) 和当前轮密钥 \(k_i\)。
\(f\) 函数的输出将被作异或掩码,用来加密左半部分输入位 \(L_{i-1}\),即与左半部分异或。
\(f\) 函数结构如图所示:
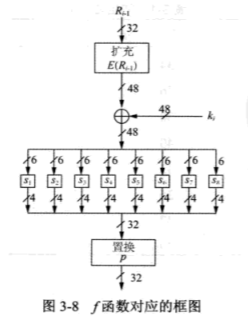
从上图可知,\(f\) 函数首先将输入分成 8 个 4 位的分组,然后将每个分组扩展为 6 位,从而将 32 位的输入扩展为 48 位。这个过程在 E-盒中进行,E-盒是一种特殊的置换。
E 盒置换 (E 扩展置换)
扩展置置换目标是IP置换后获得的右半部分R0,将32位输入扩展为48位(分为4位×8组)输出。
扩展置换目的有两个:生成与密钥相同长度的数据以进行异或运算;提供更长的结果,在后续的替代运算中可以进行压缩。
其过程如下图,即将 4 位扩展为 6 位。
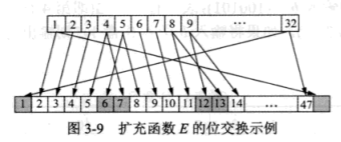
扩展置换表 E 如下:
1 | // E盒扩展置换表,将32位输入扩展至48位输出 |
可以看出,扩展的数据是从相邻两组分别取靠近的一位,4位变为6位。靠近32位的位为1,靠近1位的位为32。表中第二行的4取自上组中的末位,9取自下组中的首位。
可以发现,扩展盒增加了 DES 的扩散行为,因为某些输入位会影响两个不同的输出位置。
S 盒置换
将扩展得到的 48 位结果与轮密钥 \(k_i\) 进行异或操作,并将 8 个 6 位长的分组送入 8 个不同的 S-盒中,它将 6 位的输入映射为 4 位的输出。
具体的操作为:
1 | for (int i = 0, j = 0; i < 48; i += 6) |
以下是 8 个 S-盒:
1 | // S盒置换表,每个S盒是4x16的置换表,6位输入映射为4位输出 |
P 盒置换
将 S 盒置换得到的 32 位输出按照 P 盒进行置换,把输入的每一位映射到输出位,任何一位不能被映射两次,也不能略去。
P 盒置换表如下:
1 | // P盒置换表,32位输入映射为32位输出 |
通过以上,可以知道,轮函数总共三个步骤。
- 将 32 位输入通过 E 盒置换输出为 48 位;
- 将 48 位输出跟轮密钥进行异或,再作为 S 盒置换的输入,映射为 32 位;
- 最后将 32 位的输出作为 P 盒置换的输入,把每一位映射到输出位。
逆初始置换 \(IP^{-1}\)
合并 \(L_{16}\) 和 \(R_{16}\) 得到一个 64bits 的数据(即 \(R_{16}L_{16}\)),再经过逆初始置换一次,得到密文。
逆初始置换表如下:
1 | // 逆初始置换表 IP^(-1) |
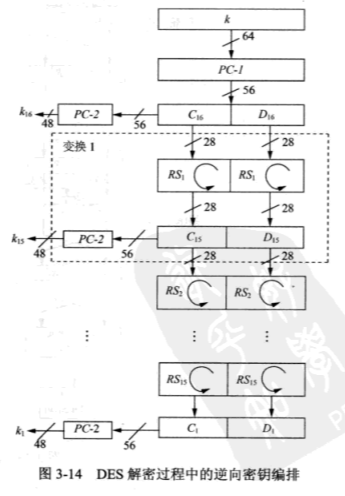
逆向密钥置换
该小节可以不作了解
因为 \(C_0=C_{16}\) 和 \(D_0=D_{16}\),因此我们可以在第一次置换后,直接得到 \(k_{16}\)。 \[ \begin{align} k_{16}&=PC-2(C_{16},D_{16})\\ &=PC-2(C_0,D_0)\\ &=PC-2(PC-1(k)) \end{align} \]
而计算 \(k_{15}\) 时,需要中间变量 \(C_{15}\) 和 \(D_{15}\),而这两个变量都可以由 \(C_{16}\) 和 \(D_{16}\) 经过循环右移得到: \[ \begin{align} k_{15}&=PC-2(C_{15},D_{15})\\ &=PC-2(RS_2(C_{16},RS_2(D_{16})))\\ &=PC-2(RS_2(C_0),RS_2(D_0)) \end{align} \] 同理,后面的轮密钥 \(k_{14},k_{13},\cdots,k_1\) 都是通过类似的方式右移得到的。
在解密模式中,每个轮密钥向右移动的位数为:
- 在解密的第 1 轮中,密钥不移位
- 在解密的第 2、9 和 16 轮中,左右两位部分均向右移动一位
- 在 3、4、5、6、7、8、10、11、12、13、14 和 15 轮种,左右两部分均向右移动两位
加密算法描述
- 将 8 字节即 64 位密钥作为输入,按照密钥置换函数 \(PC-1\) 进行压缩置换,变成 56 位
- 再将输出分为左 28 位和右 28 位的 \(C_0,D_0\),将这两部分进行 16 轮的循环左移及压缩置换 \(PC-2\),依次将上一轮的输出作为下一轮的输入,最后生成 16 个 48 位的轮密钥 (子密钥) \(k_1,k_2,\cdots,k_{16}\)
- 加密算法的输入为 64 位明文,对明文进行初始置换 \(IP\),得到 64 位输出,将其均分为左 32 位和右 32 位的 \(L_0,R_0\),将它们作为轮函数 \(f\) 的首次输入
- 轮函数将 \(R_0\) 通过 E 盒扩展置换从 32 位变为 48 位
- 扩展后的 48 位与 \(k_1\) 进行异或
- 异或后的结果再通过 S 盒置换从 48 位变为 32 位
- 将上一步的输出作为 P 盒置换的输入,得到 32 位的输出
- 将上一步的输出与左半部分进行异或运算,再将左右部分交换得到 \(L_1,R_1\)
- 重复步骤 4~8,其中轮函数的输入为上一轮的输出,共计重复 16 轮迭代,得到 \(L_{16},R_{16}\)
- 将 \(L_{16}\) 和 \(R_{16}\) 交换后合并,得到 64 位的输出 (\(R_{16}L_{16}\))
- 将输出经过一次逆初始置换 \(IP^{-1}\) 即可得到 64 位密文
解密算法描述
- 与加密算法类似,但是进行逆向密钥置换,得到密钥 \(k_{16},k_{15},\cdots,k_1\)
- 再同理将密文作为轮函数输入,但第一次轮函数过程中不与 \(k_1\) 异或,而是与 \(k_{16}\) 进行异或
- 经过 16 轮迭代后,最终得到 \(L_{16},R_{16}\)
- 将 \(L_{16},R_{16}\) 互换后合并为 64 位输出 (\(R_{16}L_{16}\))
- 再对 64 位输出经过一次逆初始置换 \(IP^{-1}\) 即可得到 64 位明文
DES 算法实现
请查看 https://github.com/HasegawaAzusa/DES
代码堪堪能运行而已,仅作示例和理解。