arnold cat 变换 (猫脸变换)

发表于 更新于 本文字数： 2k 阅读时长 ≈ 2 分钟
有关 arnold cat 变换，又称为猫脸变换、猫变换的简要笔记

猫脸变换简述

利用Arnold变换（又称猫脸变换）可以对图像进行置乱，使得原本有意义的图像变成一张无意义的图像。该变换可以在其它图像处理前对图像做预处理，例如在数字盲水印嵌入前对水印进行置乱。也可以用于普通的图像加密。

通常一次Arnold变换达不到理想效果，需要对图像进行连续多次的变换。Arnold变换具有周期性，即对图像连续进行Arnold变换，最终又能得到原图像。变换的周期和图像的尺寸有关。

当图像是一张方形的图像时，Arnold变换存在逆变换。经过N次Arnold变换后的数据可以通过N次逆变换恢复数据。

Arnold变换不仅可以用于图像置乱，也可以用于其它数据的置乱和加密。

原理

置乱的实质是新位置与旧位置的映射，且该映射是一一对应的。

下图是一次猫脸变换的示意图：

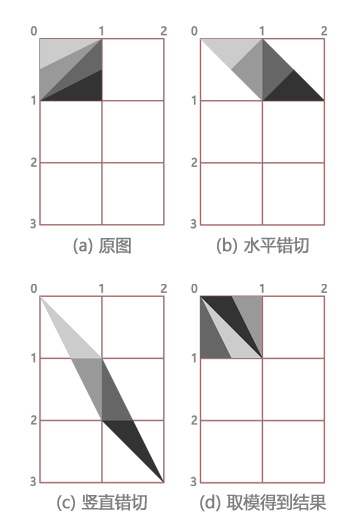
猫脸变换图解
  1. 先在 (a) 原图上做水平方向的错切
  2. 然后在 (b) 的基础上再做一次竖直方向的错切
  3. 对图像求模，即切割回填操作，便得到变换后的图像

公式

其中，\(a\)和\(b\)为给定参数，\(N\)为图片大小 (默认图片为正方形)

Arnold 变换

  • 矩阵公式 \[ \left(\begin{matrix} x'\\ y' \end{matrix}\right)= \left[\begin{matrix} 1&a\\ b&ab+1 \end{matrix}\right] \left(\begin{matrix} x\\ y \end{matrix}\right) mod(N) \]

  • 行列式公式 \[ \begin{cases} x'=(x+ay)mod(N)\\ y'=(bx+(ab+1)y)mod(N) \end{cases} \]

Arnold 逆变换

  • 矩阵公式 \[ \left(\begin{matrix} x\\ y \end{matrix}\right)= \left[\begin{matrix} ab+1&-a\\ -b&1 \end{matrix}\right] \left(\begin{matrix} x'\\ y' \end{matrix}\right) mod(N) \]

  • 行列式公式 \[ \begin{cases} x=((ab+1)x'-ay')mod(N)\\ y=(-bx'+y)mod(N) \end{cases} \]

Python 实现

以下借助了 Pillow 库实现功能

其中 a、b 为给定参数，shuffle_times 为置乱次数，reverse 为是否进行逆变换。

需要注意的是，有时候 a、b 参数互换，得到的结果不一样。

更需要注意的是，有时候 outdata[ny, nx] = indata[y, x] 需要转换为 outdata[nx, ny] = indata[x, y]，这取决于原本进行变换的时候是如何读取像素的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from PIL import Image

def arnold(infile: str, outfile: str = None, a: int = 1, b: int = 1, shuffle_times: int = 1, reverse: bool = False) -> None:
    """
    Arnold猫脸变换函数

    Parameters:
        infile - 输入图像路径
        outfile - 输出图像路径
        a - Anrold 变换参数
        b - Anrold 变换参数
        shuffle_times - 置乱次数
        reverse - 逆变换
    """
    inimg = Image.open(infile)
    width, height = inimg.size
    indata = inimg.load()
    outimg = Image.new(inimg.mode, inimg.size)
    outdata = outimg.load()

    for _ in range(shuffle_times):
        for x in range(width):
            for y in range(height):
                if reverse:
                    nx = ((a * b + 1) * x - a * y) % width
                    ny = (y - b * x) % height
                else:
                    nx = (x + a * y) % width
                    ny = (b * x + (a * b + 1) * y) % height
                outdata[ny, nx] = indata[y, x]
    
    outimg.save(outfile if outfile else "arnold_"+infile, inimg.format)

arnold("before.png", "encode.png", 9, 39, 1)
arnold("encode.png", "decode.png", 9, 39, 1, True)